10.2模拟赛

#include<bits/stdc++.h>
using namespace std;
const int N=2e5+11,M=4e5+11;
int n,ans,siz[N];
int to[M],nxt[M],id[M],edge,head[N];

inline int re_ad() {
    char ch=getchar(); int x=0,f=1;
    while(ch<'0' || ch>'9') { if(ch=='-') f=-1; ch=getchar(); }
    while('0'<=ch && ch<='9') x=(x<<1)+(x<<3)+ch-'0',ch=getchar();
    return x*f;
}

inline void addedge(int x,int y,int z) {
    ++edge,to[edge]=y,nxt[edge]=head[x],id[edge]=z,head[x]=edge;
    ++edge,to[edge]=x,nxt[edge]=head[y],id[edge]=z,head[y]=edge;
}

void dfs(int d,int f,int ff) {
    for(int i=head[d];i;i=nxt[i]) if(to[i]!=f) dfs(to[i],d,id[i]),siz[d]+=siz[to[i]];
    ++siz[d]; if(n-siz[d]==siz[d]) ans=ff;
}

int main()
{
    n=re_ad();
    for(int i=1,x,y;i<n;++i) x=re_ad(),y=re_ad(),addedge(x,y,i);
    ans=-1,dfs(1,0,0);
    printf("%d\n",ans);
    return 0;
}

 

#include<bits/stdc++.h>
using namespace std;
const int N=1e7+11,mod=1e9+7;
int n,m,fac[N],inv[N];
inline int QuickPow(int x,int y) { int res=1; for(;y;y>>=1,x=(1ll*x*x)%mod) if(y&1) res=(1ll*res*x)%mod; return res; }
int main()
{
    scanf("%d",&n);
    fac[0]=1; for(int i=1;i<=n;++i) fac[i]=(1ll*fac[i-1]*i)%mod;
    inv[n]=QuickPow(fac[n],mod-2); for(int i=n-1;i>=0;--i) inv[i]=(1ll*inv[i+1]*(i+1))%mod;
    for(m=1;(m<<1)<=n;) m<<=1;
    int ans=fac[m];
    ans=(1ll*ans*inv[n-m])%mod;
    ans=(1ll*ans*inv[2*m-n])%mod;
    ans=(1ll*ans*fac[n])%mod;
    printf("%d\n",ans);
    return 0;
}

 

 

 

 

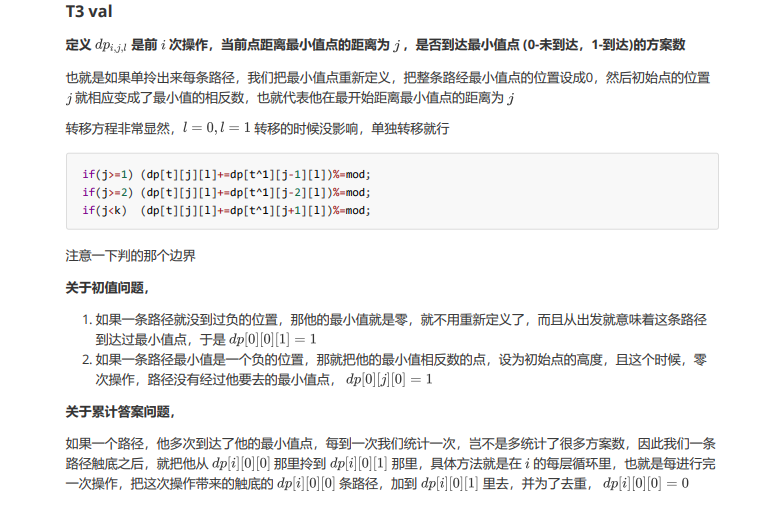
#include<bits/stdc++.h>
using namespace std;
const int N=5e3+11,mod=1e9+7;
int n,k,dp[2][N][2];
int main()
{
    scanf("%d%d",&n,&k);
    dp[0][0][1]=1; for(int j=1;j<=k;++j) dp[0][j][0]=1;
    for(int i=1,t=1;i<=n;++i,t^=1) {
        memset(dp[t],0,sizeof(dp[t]));
        for(int j=0;j<=k;++j) for(int l=0;l<=1;++l) {
            if(j>=1) (dp[t][j][l]+=dp[t^1][j-1][l])%=mod;
            if(j>=2) (dp[t][j][l]+=dp[t^1][j-2][l])%=mod;
            if(j<k)  (dp[t][j][l]+=dp[t^1][j+1][l])%=mod;
        }
        (dp[t][0][1]+=dp[t][0][0])%=mod,dp[t][0][0]=0;
    }
    int ans=0;
    for(int j=0;j<=k;++j) (ans+=dp[n&1][j][1])%=mod;
    printf("%d\n",ans);
    return 0;
}