用 Python 实现 Adaline 算法，抽取 iris 数据子集训练模型，绘制代价函数与训练次数的图像

1、通过梯度下降最小化代价函数来实现 Adaline 算法

import numpy as np

class AdalineGD():
    """通过梯度下降最小化代价函数算法实现的单层自适应线性神经网络分类器
    
    参数
    ==========
    eta: 线性学习速率，[0.0, 1.0] 上的浮点数
    n_iter: 对整个训练数据集的迭代轮数
    
    属性
    ==========
    w_: 经过训练后的权重，一维数组
    cost_: 存储每轮训练由代价函数的值，即误差平方和 
    """
    
    def __init__(self, eta=0.01, n_iter=50):
        self.eta = eta
        self.n_iter = n_iter
        
    def fit(self, X, y):
        """学习训练数据
        
        参数
        ==========
        X: 训练数据集的特征值部分，n*m的矩阵，n是样本数量，m是每个样本的特征值数量
        y: 训练数集中的每个样本的类标号，n*1的向量
        
        返回值
        ==========
        self: 通过学历训练数据的到的分类器模型
        """
        
        self.w_ = np.zeros(1 + X.shape[1])
        self.cost_ = []
        
        for i in range(self.n_iter):
            output = self.net_input(X)
            errors = y - output
            self.w_[1:] += self.eta * X.T.dot(errors)
            self.w_[0] += self.eta * errors.sum()
            cost = (errors**2).sum()/2
            self.cost_.append(cost)
        return self
    
    def net_input(self, X):
        """计算净输入"""
        z = np.dot(X, self.w_[1:]) + self.w_[0]
        return  z
    
    def activation(self, X):
        """计算线性激励函数的输出值，净输入的激励函数是净输入的简单恒等"""
        return self.net_input(X)
    
    def predict(self, X):
        """返回每轮训练预测的类标号"""
        yHat = np.where(self.activation(X) >=0, 1, -1 )

2、抽取 iris 数据子集，以不同的学习速率训练 3 个分类器模型

import numpy as np
import pandas as pd

df = pd.read_csv('D:\\pySpace\\iris.data', header=None)
y = df.iloc[:100, 4].values
y = np.where( y == 'Iris-setosa', -1, 1) # 用 if(con, T_v, F_v)的思想编码
X = df.iloc[:100, [1, 3]].values

ada1 = AdalineGD(eta=0.01, n_iter=10).fit(X, y)
ada2 = AdalineGD(eta=0.001, n_iter=10).fit(X, y)
ada3 = AdalineGD(eta=0.0001, n_iter=10).fit(X, y)

3、分别绘制以上三个模型中，代价函数和训练次数的图像

from matplotlib import pyplot as plt
%matplotlib inline

models = [ada1, ada2, ada3]
fig, ax = plt.subplots(nrows=1, ncols=3, figsize=(21, 7))

for i, model in enumerate(models):   
    ax[i].plot(range(1, len(model.cost_) + 1), model.cost_, marker='o')
    ax[i].set_title('学习速率 ' + str(model.eta), fontsize=19)
    ax[i].set_xlabel('训练次数', fontsize=17)
    ax[i].set_ylabel('误差平方和', fontsize=17)
    ax[i].tick_params(labelsize=15)

图形如下：

 

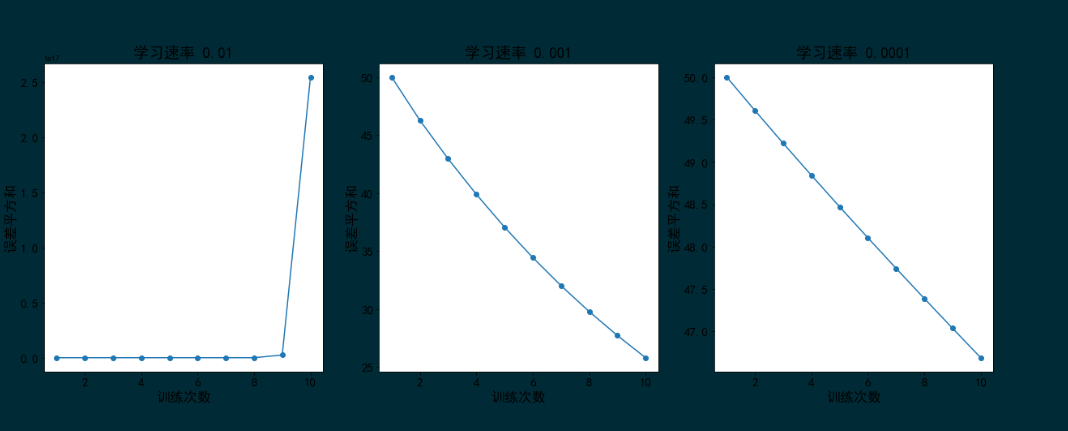
从代价函数输出结果图像可以看出，学习速率过大会因为算法跳过最优解，导致误差随着迭代次数的增加而增大；学习速率太小时，为了达到算法收敛的目标，需要迭代的次数更多。