Transformer结构简谈
Transformer结构简谈
本文的参考资料如下。
引言
在Transformer出来之前,在自然语言处理(Natural Language Processing,NLP)领域经常使用循环神经网络(RNN)和长短期记忆网络(LSTM)等模型来处理序列数据。
2017年,谷歌(Google)在论文《Attention Is All You Need》中提出了Transformer架构,彻底改变了NLP领域。
Transformer是一个编码器—解码器(Encoder-Decoder)架构的模型,论文中的编码器层是由6个编码器堆叠在一起的,解码器层也一样。
编码器-解码器架构的大体思想就是把整个输入先编码成一个或者一组向量,然后利用这些向量解码生成输出,包含了编码器和解码器这两个主要的部分。
编码器用来接收输入的序列,然后将输入序列中的每个元素映射为一个向量。供解码器使用。
解码器初始从编码器的输出出发,通常是自回归(Autoregressive)的,在每一步输出一个元素之后,把前面的输出作为下一步的输入。
在Transformer中,每一个编码器和解码器的内部结构如下图1所示。
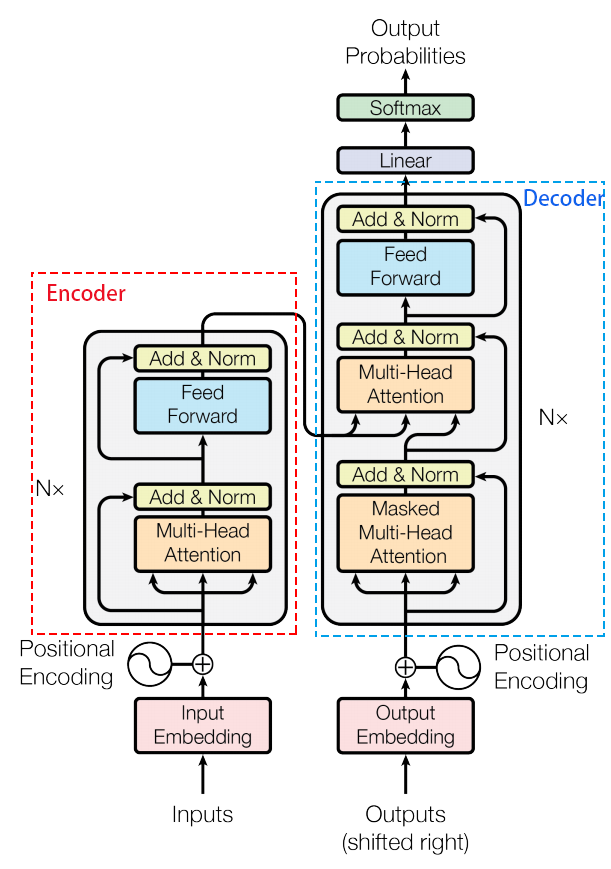
图1:Transformer结构示意图
可以看到,编码器包含了两层,一个自注意力(Self-Attention)层和一个前馈神经网络层,自注意力机制可以帮助当前节点不仅仅关注当前的词,从而获取到上下文的语义。
解码器中也包含了编码器中提到的那两层网络,但是在这两层中间还有一层注意力(Attention)层,帮助当前节点获取到当前需要关注的重点内容。
编码器层结构
首先,模型会对输入的数据进行嵌入(Embedding)操作,也就是将原始输入转换为向量形式,把离散的单词映射到连续空间中的向量。
在嵌入结束之后,输入到编码器层,自注意力机制处理完数据之后会把数据送到前馈神经网络,这里的前馈神经网络的计算可以并行,得到的输出会输入到下一个编码器,如下图2所示。
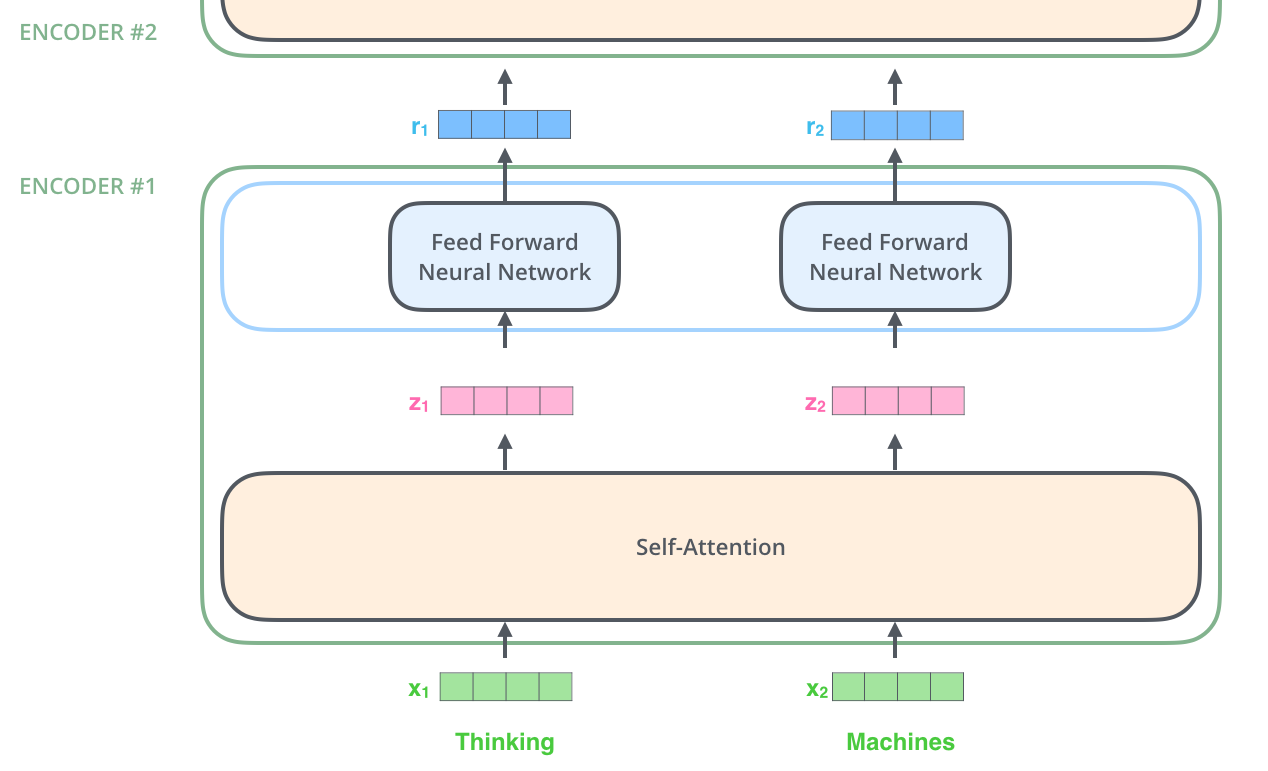
图2:编码器层结构示意图
位置编码
Transformer不像RNN那样按照顺序进行处理,没有CNN那样的局部窗口感知,它一次性把整个句子所有的token一起处理,本身没有顺序信息。
比如,如果我们输入“I love you”和“You love I”,在没有任何顺序信息的情况下,它们得到的结果是一样的。
因此,我们需要位置编码(Positional Encoding)。
位置编码的维度和嵌入的维度一样,这个向量采用了一种很独特的方式来学习到这个值,这个向量可以决定当前词的位置,或者说在同一个句子中的不同词之间的距离。
在论文中的计算方式如下。
- 对于偶数维度(\(2i\)),使用正弦函数:\[PE(pos, 2i) = \sin\left(\frac{pos}{10000^{2i/d_{model}}}\right) \]
- 对于奇数维度(\(2i+1\)),使用余弦函数:\[PE(pos, 2i+1) = \cos\left(\frac{pos}{10000^{2i/d_{model}}}\right) \]
其中,\(pos\) 表示词在序列中的位置,\(i\) 表示当前维度,\(d_{model}\) 是嵌入向量的维度。这样设计的位置编码能够让模型捕捉到序列中词语之间的相对和绝对位置信息。
最后,我们把这个位置编码和嵌入的值相加,作为输入送到下一层。
自注意力机制(Self Attention)
自注意力机制的思想和注意力机制的思想差不多,但是自注意力机制是Transformer用来把其它相关单词的“理解”转换成我们正在处理的单词的一种思路。
对于句子“The animal did not cross the street because it was too tired”,这里的“it”到底代表的是“animal”还是“street”呢?
对于我们人类来说,这很简单,但是对于机器来说这是很困难的,接下来看自注意力机制的处理过程,这里十分重要!
- 首先,自注意力机制计算出三个新的向量,在原始的论文中的向量的维度是512维,这三个向量分别命名为Query、Key和Value,这三个向量是Embedding向量和一个矩阵相乘得到的结果,这个矩阵是随机初始化的,维度是[64, 512],如下图3所示。
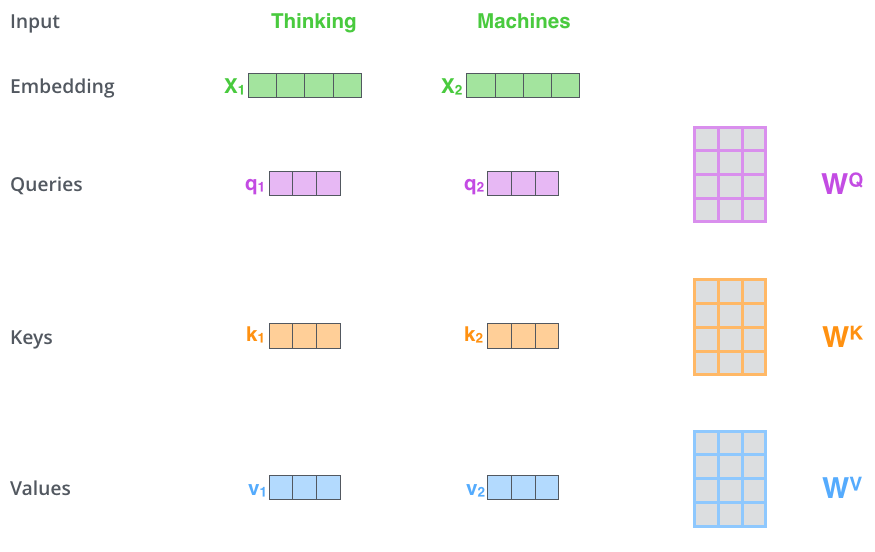
图3:自注意力机制示意图
- 计算自注意力机制的分数值,这个分数值决定了我们在某一个位置编码一个词的时候,对输入的句子的其它部分的关注程度,这个分数值的计算方式是Q和K进行点乘,如下图4所示。
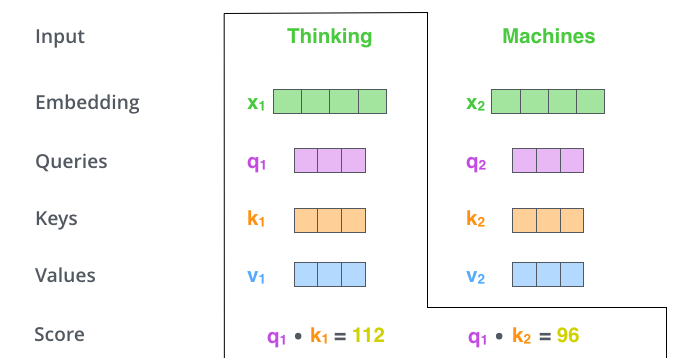
图4:自注意力机制分数计算示意图
- 接下来把这个值除以一个常数,把得到的结果做一个Softmax计算,得到的结果就是每个词对于当前位置的词的相关性的大小,当然,当前位置的词的相关性肯定会很大。具体示例如下图5所示。
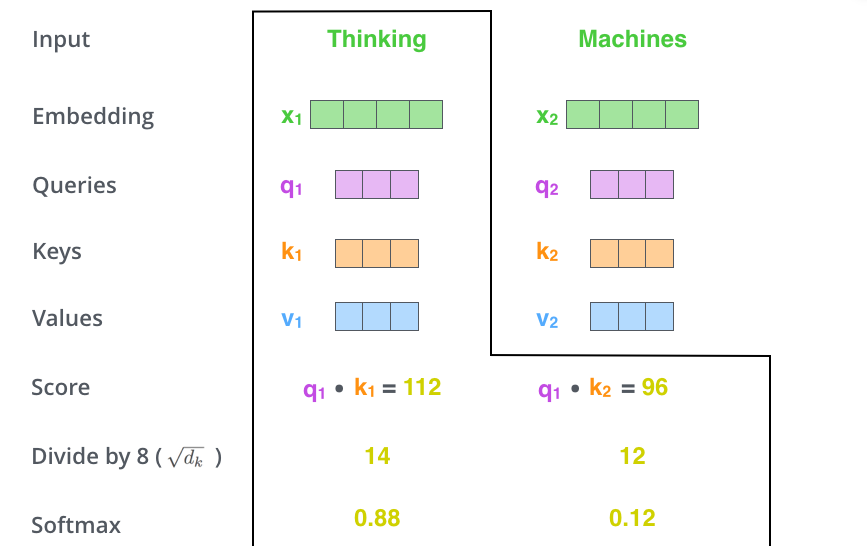
图5:自注意力机制Softmax计算示意图
- 下一步就是把V和Softmax得到的数值进行相乘,然后相加,得到的结果就是自注意力机制在当前位置的数值,如下图6所示。
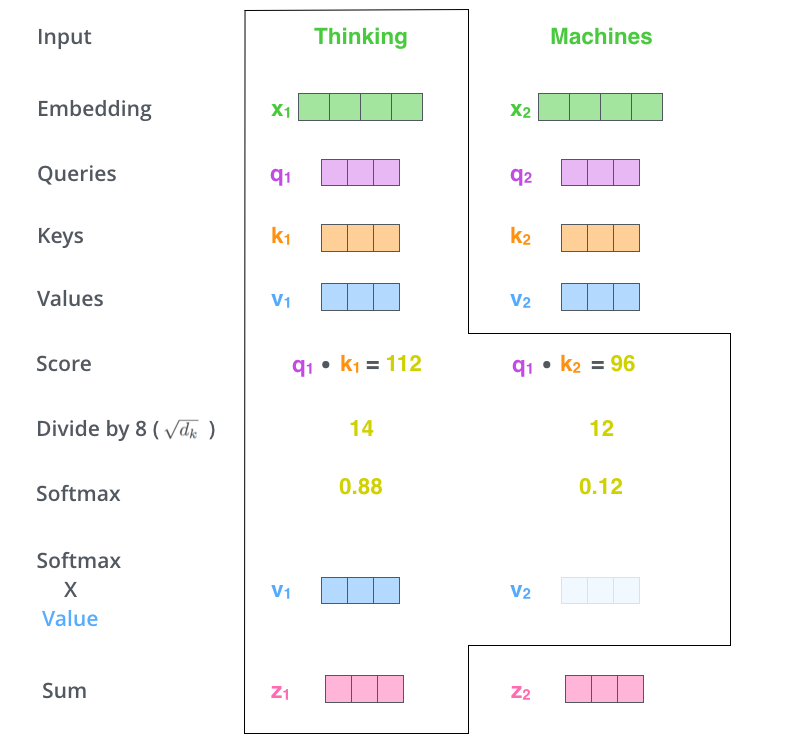
图6:自注意力机制输出计算示意图
在实际的应用中,为了提高计算的速度,我们使用矩阵,直接计算出Q,K,V的矩阵,然后将Embedding和三个矩阵相乘,然后把新得到的Q,K相乘,乘以一个常数,做Softmax,最后在乘上V即可。
这种通过Q和K的相似度来确定V的权重分布的方法在论文中被称为“Scaled Dot-product Attention”
原理图如下图7、8所示。
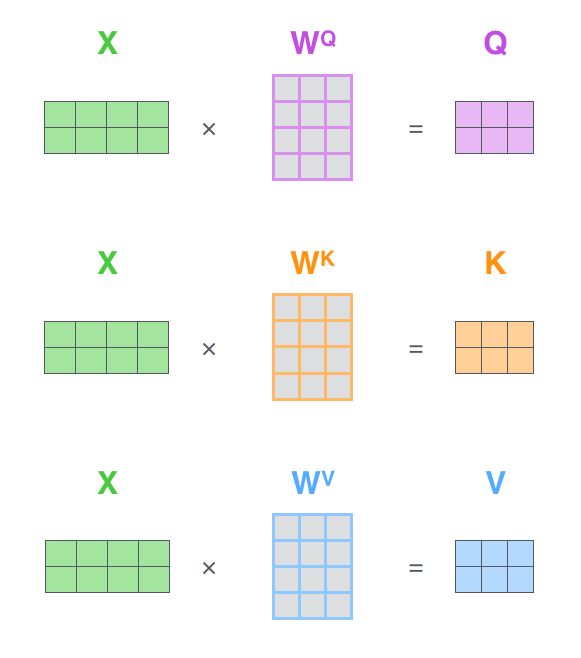
图7:Q、K、V矩阵
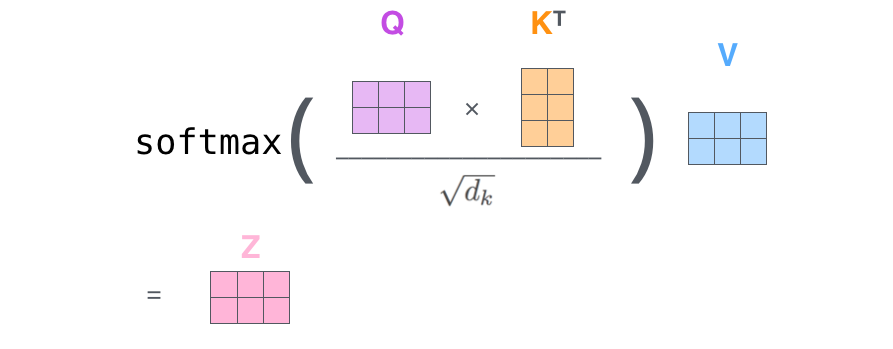
图8:Attention计算公式
多头注意力机制(Muti-head Attention)
论文中另外一个十分巧妙的地方是给自注意力加入了一个叫做“多头注意力”的东西。
多头注意力可以理解为不仅仅只初始化一组Q、K、V,而是初始化多组,在论文中使用了8组,所以结果是得到了8个矩阵。
该部分如下图9、10所示。
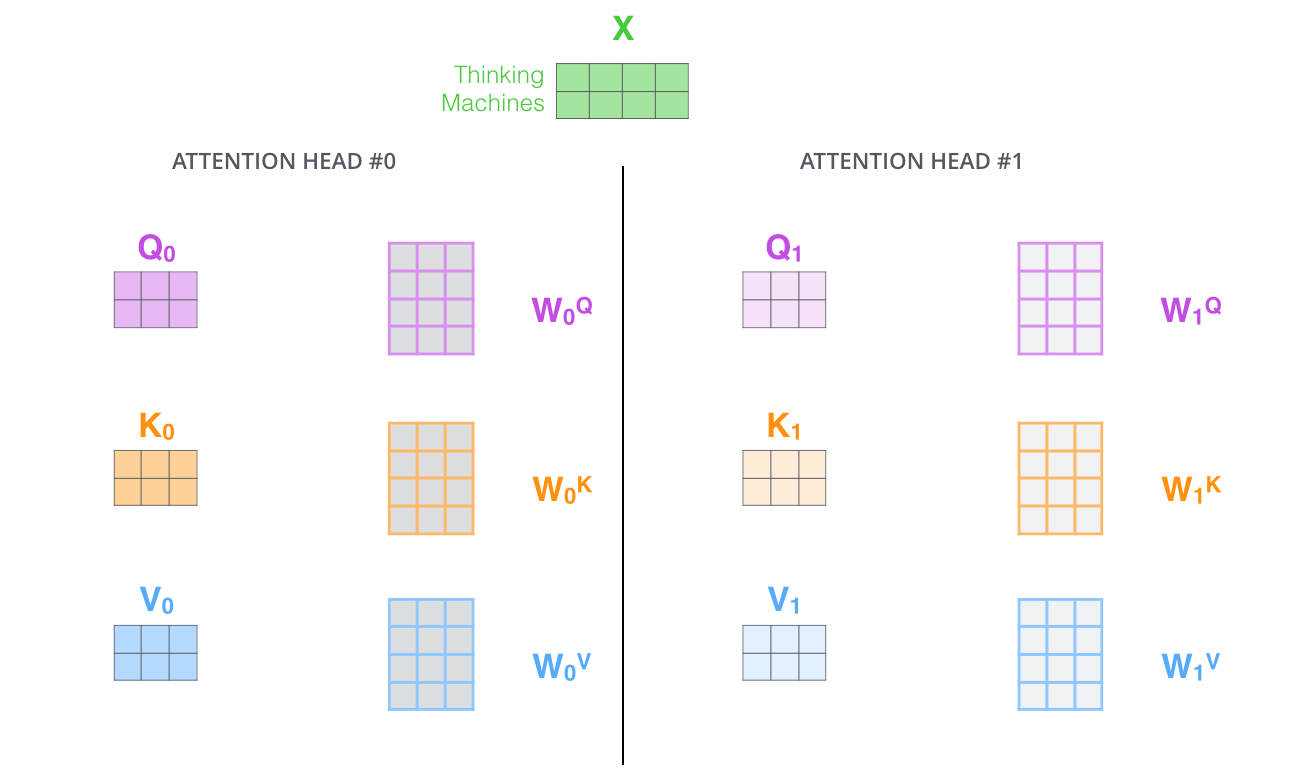
图9:多头注意力机制中初始化多个Q、K、V
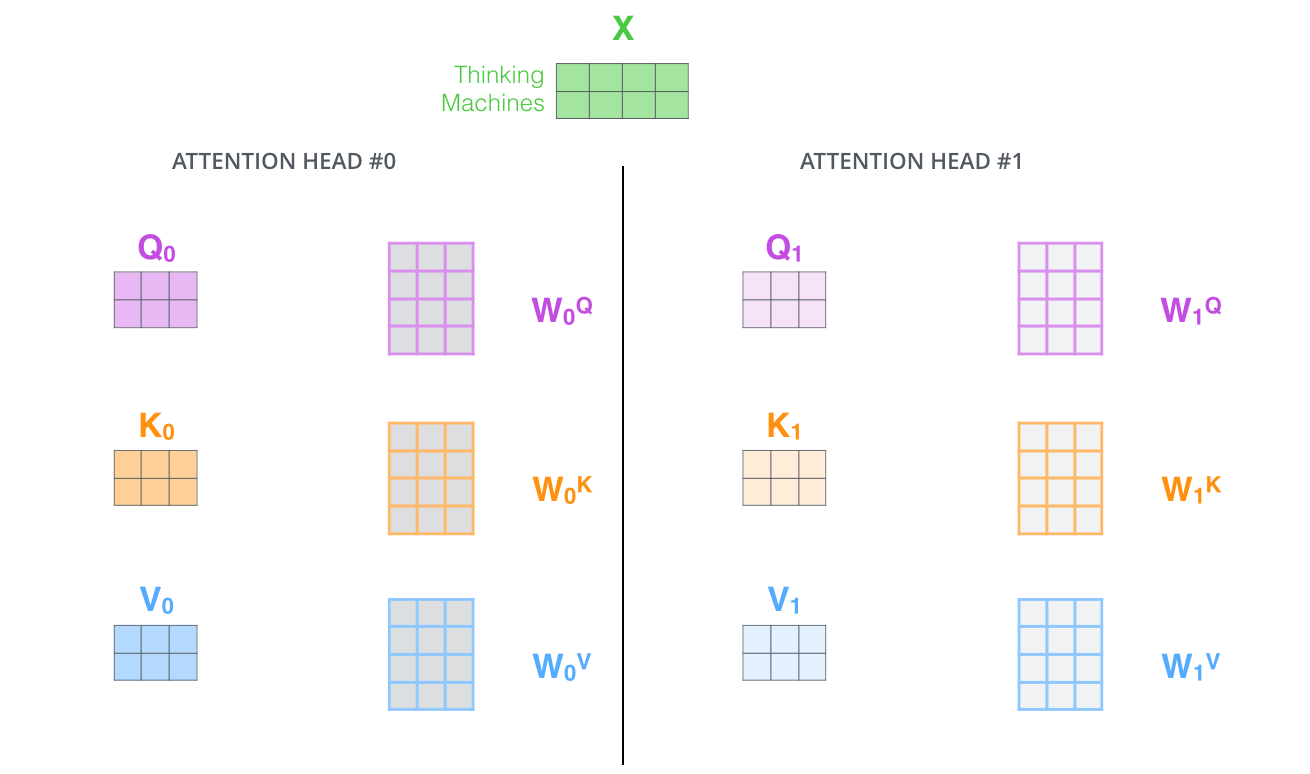
图10:多头注意力机制中并行计算多个头
层归一化(Layer Normalization)
在Transformer中,每一个子层(Self-Attention、FFN)之后都会连接一个残差模块,有一个层归一化,如下图11所示。
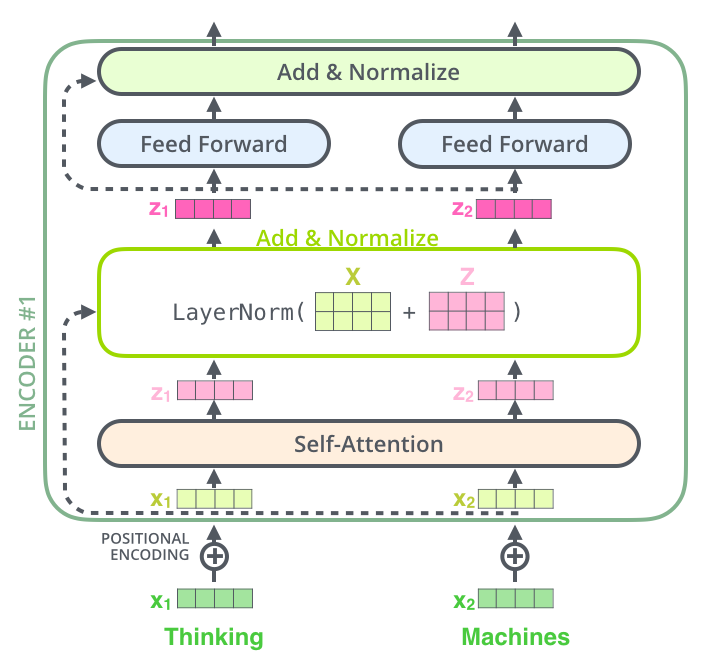
图11:层归一化示意图
归一化的目的就是输入变成比均值为0、方差为1的数据,是为了不让我们的输入落在激活函数的饱和区。
批量归一化(Batch Normalization)的思想是在每一层的每一批数据上都进行归一化。
我们可能对输入的数据进行归一化,但是经过该网络层的作用之后,我们的数据不再是归一化的了,数据的偏差越来越大,反向传播需要考虑到大偏差,我们只能使用较小的学习率来防止梯度消失或者梯度爆炸。
批量归一化就是针对每一小批数据,在“批”这个方向上做以归一化。
层归一化是在每一个样本上计算均值和方差,公式如下。
其中:
- \(x_i\):输入的第 \(i\) 个特征
- \(\mu_L\):当前层所有特征的均值
- \(\sigma_L^2\):当前层所有特征的方差
- \(\epsilon\):防止分母为零的小常数
- \(\alpha\) 和 \(\beta\):可学习的缩放和偏移参数
这两种归一化方法的对比如下图12所示。
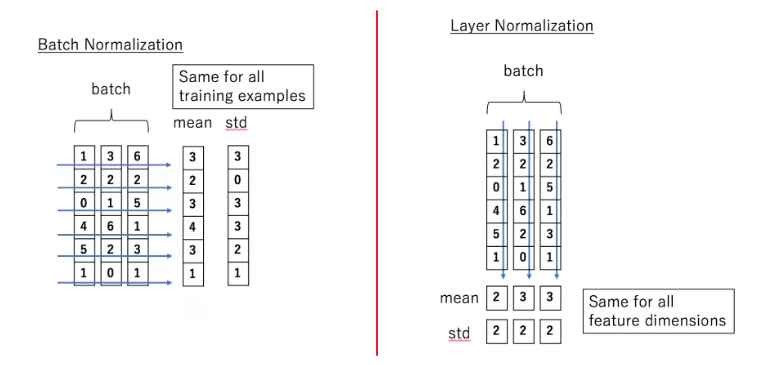
图12:批量归一化与层归一化对比示意图
前馈神经网络(Feed Forward Network)
前馈神经网络没办法输入8个矩阵,我们需要把8个矩阵降为1个,把8个矩阵拼成1个大矩阵,然后随机初始化1个矩阵和这个拼成后的相乘,得到1个最终的矩阵。
这里的具体过程如下图13所示。
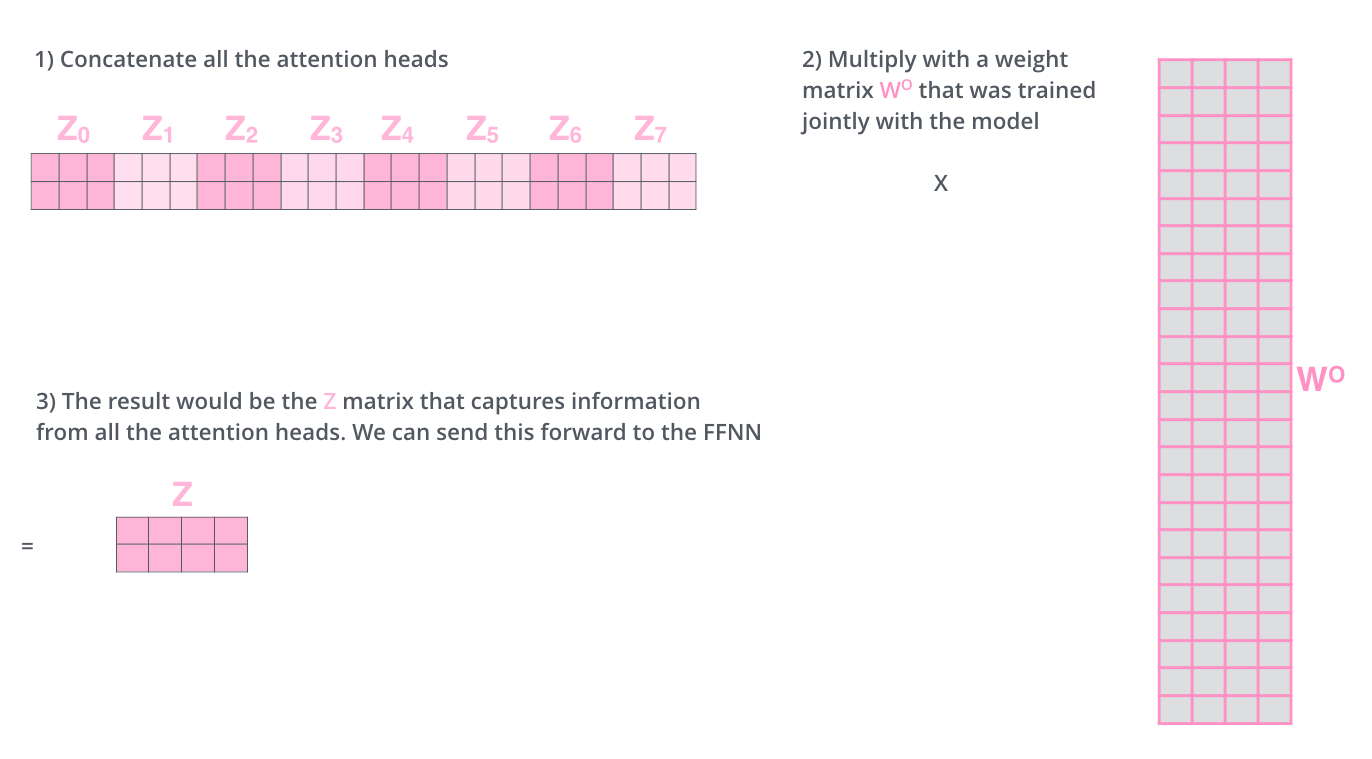
图13:前馈神经网络结构示意图
解码器层结构
解码器和编码器大同小异,首先是添加一个位置编码,然后是一个叫做Masked Muti-head Attention的东西,其余层的结构和编码器一样。
掩码多头注意力机制(Masked Muti-head Attention)
在训练时,解码器是自回归的,即当前时刻的输出只能依赖之前时刻的输出,不能依赖未来信息(否则就是“作弊”)。
在推理时,解码器是逐步生成的,必须保证每次只看到历史信息。
Mask表示掩码,对某些部分进行掩盖,使其在参数更新的时候不产生效果。论文中涉及到了两种——填充掩码(Padding Mask)和序列掩码(Sequence Mask)。
Padding Mask指的是对输入序列中的填充部分进行掩盖。由于输入序列长度不一致,通常会在较短的序列后面补零,使其长度一致。为了避免模型在计算注意力分数时关注这些填充位置,需要使用Padding Mask将这些位置的注意力分数设为极小值,从而在Softmax后这些位置的权重为零,不参与后续计算。
Sequence Mask用于保证解码器在生成序列时,每个位置只能看到当前位置及其之前的内容,不能看到未来的信息。这样可以防止模型在训练时“偷看”后面的词,实现自回归生成。具体做法是在注意力分数矩阵中,将未来位置的分数设为极小值,确保每一步只能依赖已生成的内容。
通过这两种Mask机制,解码器能够有效地处理变长输入和自回归生成的需求,保证模型训练和推理的合理性。
流程总结
编码器通过处理输入序列开启工作,顶端编码器输出后会变转化为一个包含向量K和V的注意力向量集,这是并行化操作,如下图14所示。
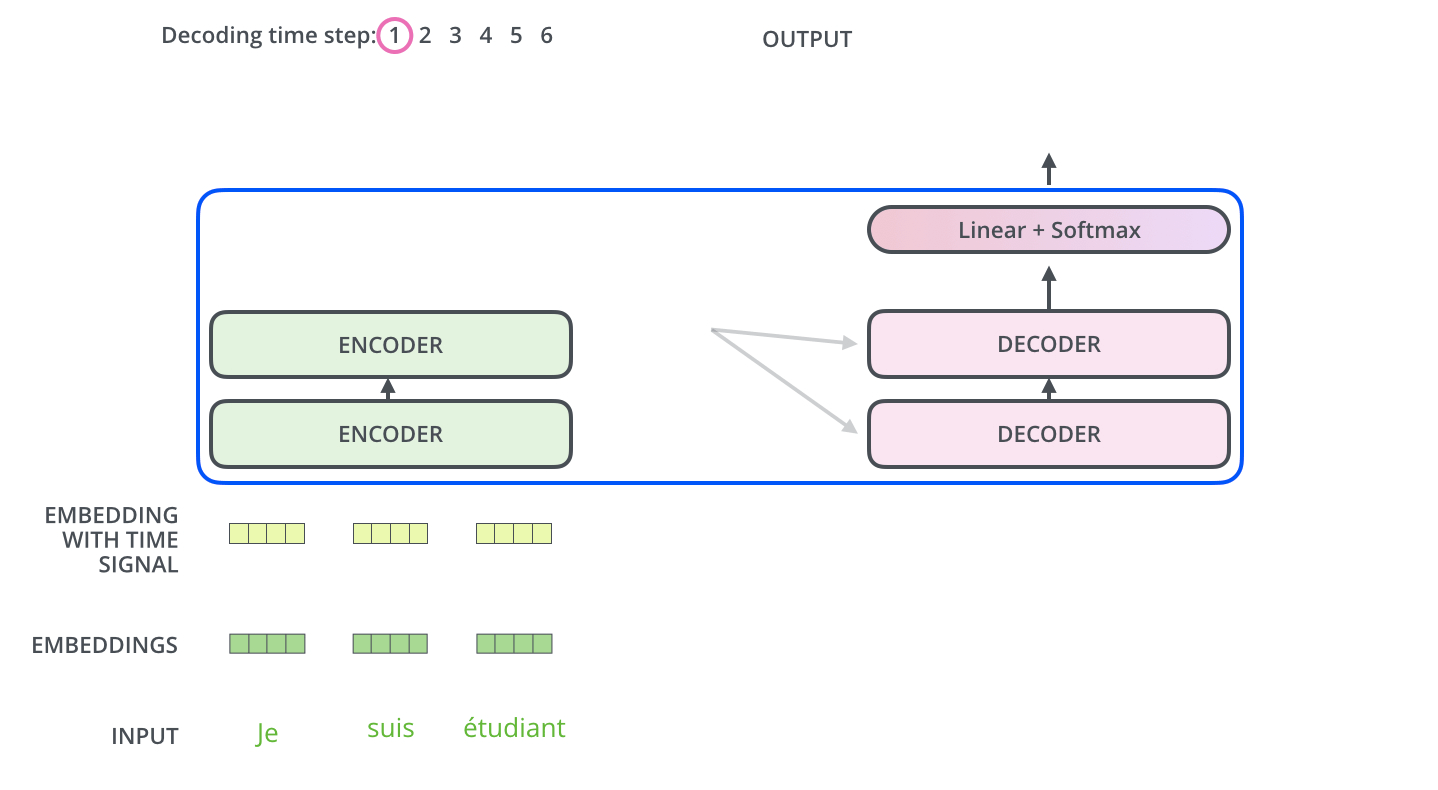
图14:编码器输出示意图
完成编码阶段后,则开始解码阶段。解码阶段的每个步骤都会输出一个输出序列(在这个例子里,是英语翻译的句子)的元素。
接下来的步骤重复了这个过程,直到到达一个特殊的终止符号,它表示解码器已经完成了它的输出。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号