CPLEX 初识 -- JAVA实现
CPLEX 初识 -- JAVA实现
本文参考《运筹优化常用模型、算法及案例实战》,同时也是笔者用来记录自己所学知识,如有问题欢迎交流讨论~
1 环境配置&模型建立
需要装配jar包及配置VM options, 如下图所示:
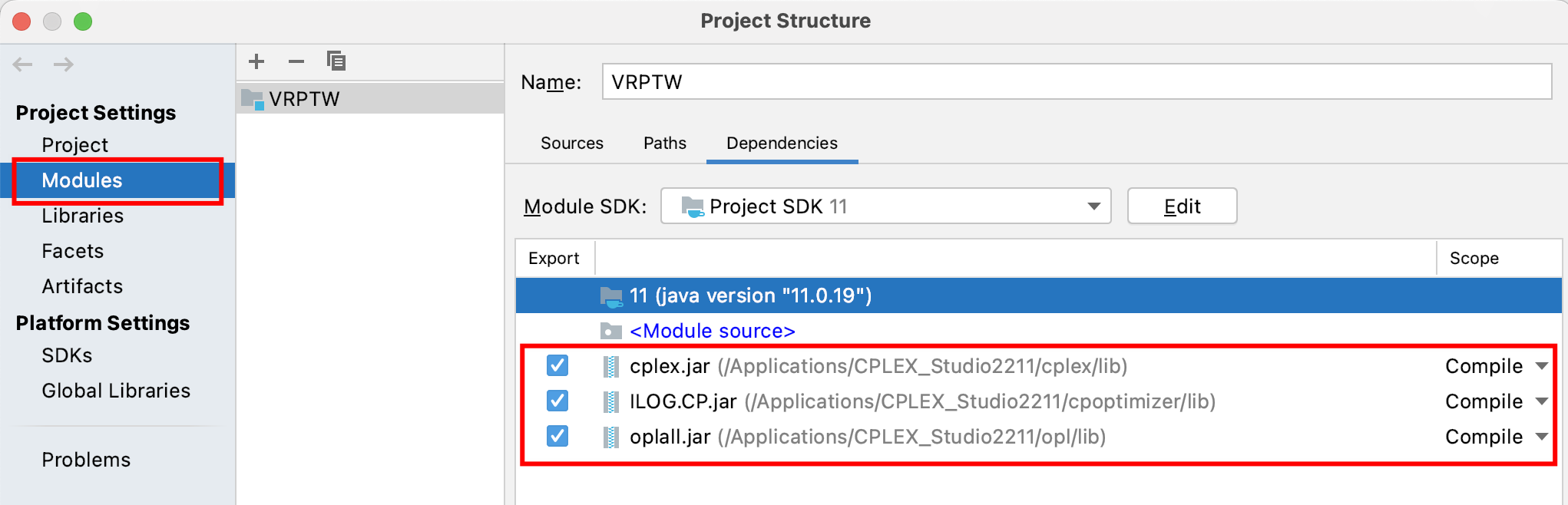
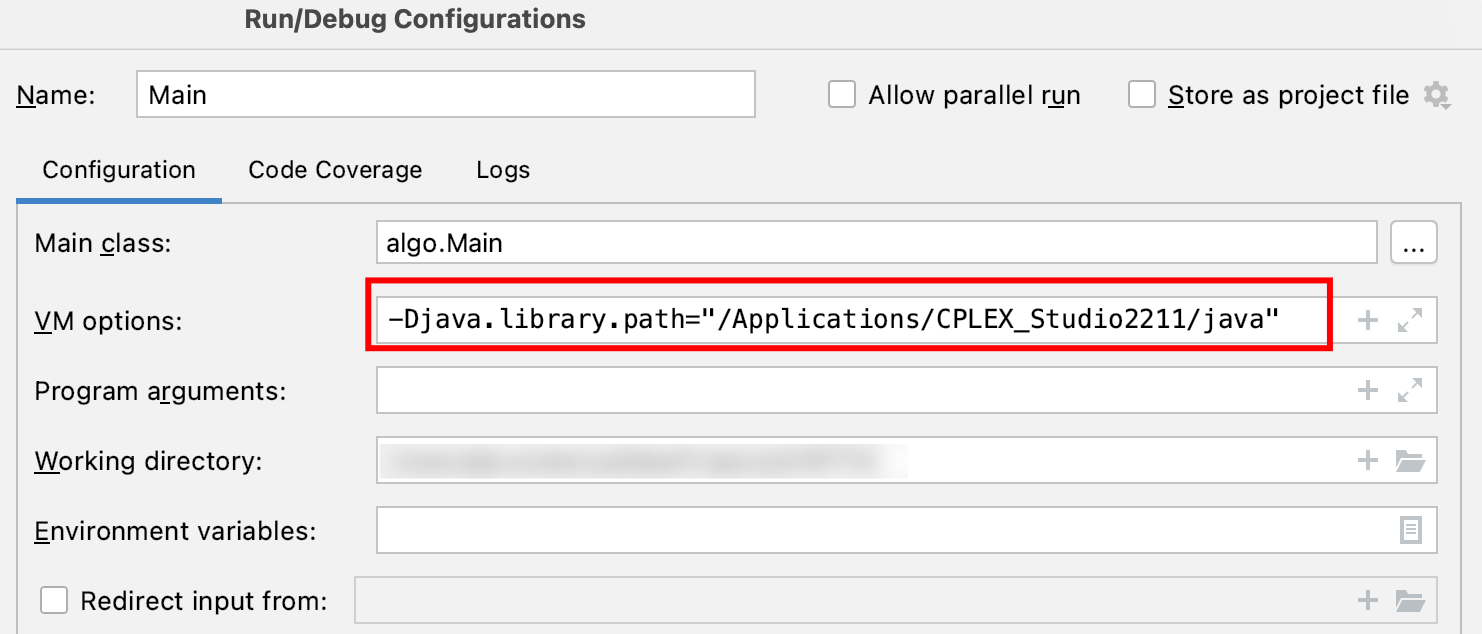
-Djava.library.path="/Applications/CPLEX_Studio2211/java"
一般使用IloCplex model = new IloCplex(); //建立cplex对象新建模型
2 变量
//变量类型
// IloNumVarType.Bool;
// IloNumVarType.Int;
// IloNumVarType.Float;
//创建变量
// model.numVar(lb, ub, type, name); //一般变量创建方法
// model.intVar(); //创建整数变量
// model.boolVar(); //创建0-1变量
// model.numVarArray(); //以数组形式创建一般变量
// model.intVarArray(); //以数组形式创建整数变量
// model.boolVarArray(); //以数组形式创建0-1变量
3 表达式
通常由两种方法:
- 表达式较为简单时,可以使用基本的
IloModeler中的方法(例如加、减、乘、数量积等)定义。注:IloCplexs已继承该接口,故可以直接通过IloCplexs对象进行调用。
//常用表达式
// model.sum();
// model.prod();
// model.scalProd(); //数组与数组之间的数量积
// model.diff();
// model.negative(); //乘以-1
// model.square(); //表达式的square
- 表达式略复杂时,使用
IloNumExpr 接口和IloLinearNumExpr接口中的方法定义。
4 范围约束
使用IloRange对象表示形如lb <= expression <= ub的约束。
// IloRange rng1 = model.range(lb, expr, ub, name); //表示lb<=expr<=ub
// IloRange rng2 = model.le(expr, ub, name); //表示 expr <= ub ~ 也可直接model.addLe();
// IloRange rng3 = model.ge(expr, lb, name); //表示 expr >= lb ~ 也可直接model.addGe();
5 目标函数
// IloObjective obj = model.addMaximize(expr); //方式一
// IloObjective obj = model.add(model.maximize(expr)); //方式二
6 建模方式
该部分通过一个简单的案例,主要介绍两种建模方式:行建模与列建模。
案例:在已知各种Food所含Nutrition的前提下,各样Food需买多少,以满足营养需求及各类容量约束。信息见下表:
| Food 1 | Food 2 | Nutrition最小需求量 | Nutrition最大需求量 | |
|---|---|---|---|---|
| Nutrition 1 | $$a_{11}$$ | $$a_{12} $$ | nutrMin[1] | nutrMax[1] |
| Nutrition 2 | $$a_{21}$$ | $$a_{22}$$ | nutrMin[2] | nutrMax[2] |
| Food最小数量 | foodMin[1] | foodMax[1] | ||
| Food最大数量 | foodMin[2] | foodMax[2] | ||
| Food单位成本 | foodCost[1] | foodCost[2] |
该表使用数据结构的方式编写如下:
private static class Data {
int nFoods; //Food总种类 ~ 决定了几个决策变量
int nNutrs; //Nutrition总种类 ~ 决定了m条约束
int[] foodMin; //各样food的最小数量
int[] foodMax; //各样food的最大数量
float[] foodCost; //各样food的成本
int[] nutrMin; //各样Nutrition的最小需求量
int[] nutrMax; //各样Nutrition的最大需求量
int[][] a_ij; //Food j中含有Nutrition i的数量
// 以下是constructor
public Data(int[] foodMin, int[] foodMax, float[] foodCost, int[] nutrMin, int[] nutrMax, int[][] a_ij) {
this.foodMin = foodMin;
this.foodMax = foodMax;
this.foodCost = foodCost;
this.nutrMin = nutrMin;
this.nutrMax = nutrMax;
this.a_ij = a_ij;
this.nFoods = foodMin.length;
this.nNutrs = nutrMin.length;
}
}
6.1 行建模
- 决策变量为:\(buy[j]\)表示\(Food[j]\)买多少,是整数变量。
- 约束条件:
- \(Nutrition[j],j\in\{1,2,...,m\}\) 最小满足量和最大满足量要求;即 \(nutrMin[i] \leq\sum_j a_{ij}*buy_j \leq nutrMax[i], \forall i\in\{1,2,...,m\}.\)
- \(Food[j],j\in\{1,2,...,n\}\)最小数量和最大数量要求。(可以在创建变量时直接添加)
- 目标函数:成本最低。
// (1)行建模
static void buildModelByRow(Data data) throws IloException {
// 新建模型
IloCplex model = new IloCplex();
// 变量: buy[j] j \in {1,2,...,nFoods}
int nFoods = data.nFoods; //变量个数
IloNumVar[] buy = new IloNumVar[nFoods]; //创建变量数组,下对变量进行具体创建
for (int j = 0; j < nFoods; j++) {
buy[j] = model.numVar(data.foodMin[j], data.foodMax[j], IloNumVarType.Int, "buy_j");
}
// 约束条件
int nNutrs = data.nNutrs;
for (int i = 0; i < nNutrs; i++) {
IloLinearNumExpr expr = model.scalProd(data.a_ij[i], buy); //\sum_j a_ij*buy_j
model.addRange(data.nutrMin[i],expr,data.nutrMax[i]);
}
// 目标函数
model.addMinimize(model.scalProd(data.foodCost,buy));
}
6.2 列建模
按列添加本质上是添加变量,在添加的过程中需要考虑:1. 对目标函数的影响。2. 对约束的影响。实现过程如下:
- 使用
model.column(IloObjective,coefficient)向该列添加对应的目标函数系数,返回一个列对象col1; - 使用
model.column(IloRange constraint[i],double val)向该列添加对应的约束的系数,同样返回一个列对象col2。 - 之后通过
col = col1.and(col2)将两列对象进行”连接“,完成对目标函数和约束的更新。 - 使用
model.numVar(IloColunmn col, double lb, double ub, IloNumVarType type)为以上创建的列col设置对应的变量(其中需要输入上下界及变量类型)。
// (2)列建模
static void buildModelByColumn(Data data) throws IloException {
// 新建模型
IloCplex model = new IloCplex();
// 创建m条约束 和 n个变量
int nNutrs = data.nNutrs;
IloRange[] constraints = new IloRange[nNutrs]; // m条约束
IloNumVar[] buys = new IloNumVar[data.nFoods]; // n个变量
for (int i = 0; i < nNutrs; i++) { // 对约束设置上下界
constraints[i] = model.addRange(data.nutrMin[i],data.nutrMax[i]);
}
// 向约束和目标函数中加入对应的系数,并创建变量
IloObjective cost = model.addObjective(null);
for (int j = 0; j < data.nFoods; j++) { //加n条列
IloColumn col_j = model.column(null); //j对应的列对象,后需要由obj+cons合成
IloColumn col_obj = model.column(cost, data.foodCost[j]);
for (int i = 0; i < nNutrs; i++) {
IloColumn col_constaints_i = model.column(constraints[i], data.a_ij[i][j]);
col_j = col_obj.and(col_constaints_i);
}
// 对新加的列 创建变量
buys[j] = model.numVar(col_j, data.foodMin[j], data.foodMax[j]);
}
}
6.3 案例练习
编译实现如下线性规划:
\[\begin{alignat}{2}
\max \quad &x_1+2x_2+3x_3 \tag{1} \\
\mbox{s.t.}\quad &-x_1+x_2+x_3\leq 20 \tag{2}\\
&x_1-3x_2+x_3\leq30 \tag{3} \\
&0\leq x_1\leq40, x_2,x_3\geq 0. \tag{4}
\end{alignat}
\]
代码如下:
//3 案例练习
static void practice() throws IloException {
// 创建模型, 输入系数
IloCplex model = new IloCplex();
double[] obj_coeffs = {1.0, 2.0, 3.0};
double[] v_lb = {0.0, 0.0, 0,0};
double[] v_ub = {40.0, Double.MAX_VALUE, Double.MAX_VALUE};
// Step1 变量
String[] x_name = {"x_1","x_2","x_3"};
IloNumVar[] x = model.numVarArray(3, v_lb, v_ub,x_name);
// Step2 约束
int m = 2; //两条约束
double[][] a = {{-1, 1, 1}, {1, -3, 1}}; //变量前系数 A = [a_ij]
double[] b = {20,30};
for (int i = 0; i < m; i++) {
model.addLe(model.scalProd(a[i],x),b[i]);
}
// Step3 目标函数
model.addMaximize(model.scalProd(obj_coeffs,x));
}
7 模型求解及输出
7.1 求解
model.solve()
7.2 解状态
IloCplex.Status status = model.getStatus();
System.out.println(status);
解类型如下:
- Bounded
- Unbounded
- Feasible
- Infeasible
- InfeasibleOrUnbounded
- Error
- Unknown
- Optimal
7.3 获取obj、变量、约束相关信息
(1)获取obj_value
double objValue = model.getObjValue();
System.out.println("obj_value = " + objValue);
(2)获取变量值:单个/多个
double x_0_value = model.getValue(x[0]);//获取单个变量值
System.out.println("x_0 = " + x_0_value);
double[] x_values = model.getValues(x);//获取多个变量值
for (int i = 0; i < x_values.length; i++) {
System.out.println("x_" + i + " = " + x_values[i]);
}
(3)获取变量对应的reduced cost
double[] reducedCosts = model.getReducedCosts(x);
System.out.print("Reduced Costs = ");
for (double r_c: reducedCosts) {
System.out.print(r_c + " ");
}
System.out.println();
(4)获取约束对应的松弛变量
double[] slacks = model.getSlacks(consts);
System.out.print("Slack Variables = ");
for (double s : slacks) {
System.out.print(s + " ");
}
System.out.println();
(5)获取约束对应的对偶变量
double[] duals = model.getDuals(consts);
System.out.print("Dual Variables = ");
for (double d : duals) {
System.out.print(d + " ");
}
System.out.println();
(6)获取模型/对偶模型的极射线
// model.getRay();
// model.dualFarkas();
(7)模型导出与导入
model.exportModel("practice.lp"); //导出
model.importModel("practice.lp"); //导入
运行结果如下:

模型导出结果:

8 参数
官方介绍:https://www.ibm.com/docs/zh/icos/12.10.0?topic=cplex-list-parameters
此处待补充具体常用参数。(后续补充)
写在最后
Like a city that is broken down and without walls is a man whose spirit is without restraint.




 浙公网安备 33010602011771号
浙公网安备 33010602011771号