2.＜tag-二叉树和层序遍历相关题＞-lt.116. 填充每个节点的下一个右侧节点指针 + lt.117. 填充每个节点的下一个右侧节点指针 II

lt.116. 填充每个节点的下一个右侧节点指针

[案例需求]

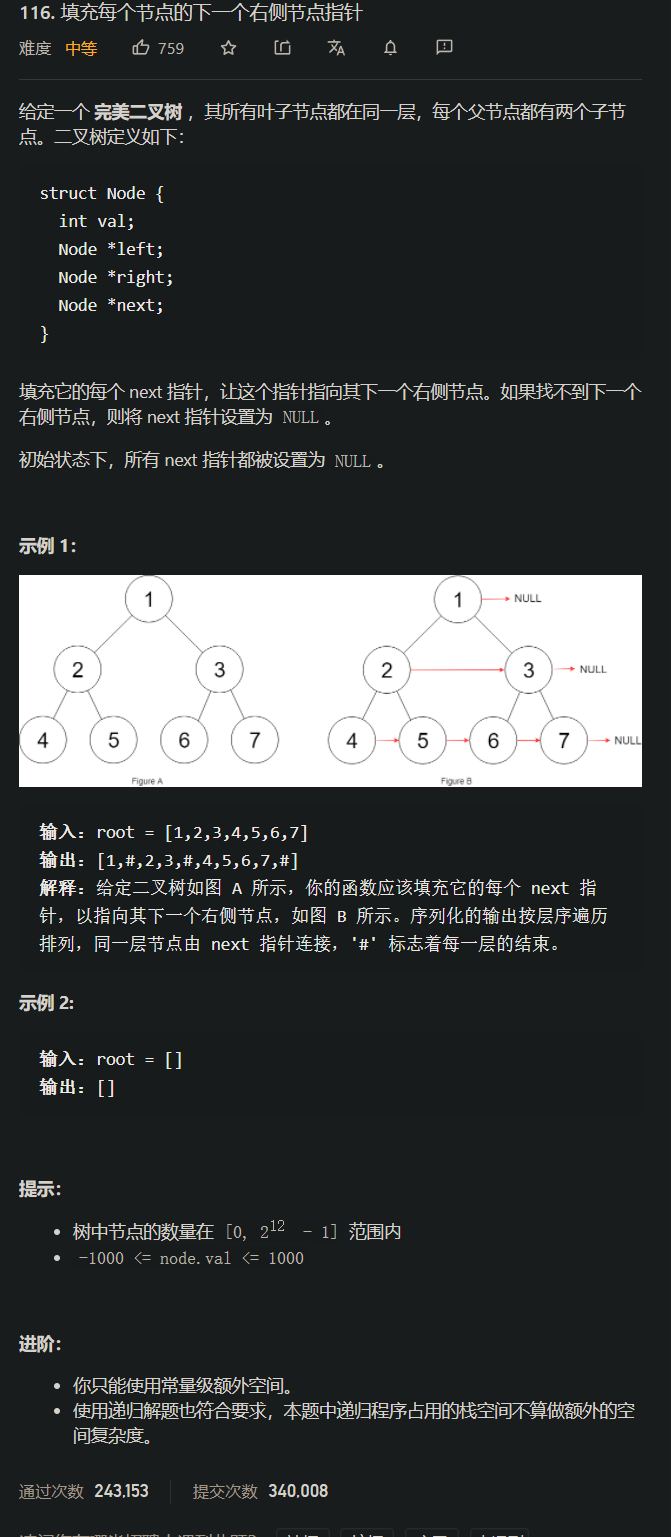
[思路分析一, 迭代法]

[代码实现]

/*
// Definition for a Node.
class Node {
    public int val;
    public Node left;
    public Node right;
    public Node next;

    public Node() {}
    
    public Node(int _val) {
        val = _val;
    }

    public Node(int _val, Node _left, Node _right, Node _next) {
        val = _val;
        left = _left;
        right = _right;
        next = _next;
    }
};
*/

class Solution {
    public Node connect(Node root) {
        //层序遍历, queue存储, 
        Queue<Node> queue = new ArrayDeque<>();
        if(root == null)return root;
        queue.add(root);
        Node res = root;
        // 目的是每一层连接起来
        while(!queue.isEmpty()){
            int size = queue.size();

            for(int i = 0; i < size; i++){
                root = queue.poll();
                
                //把每一层的结点连接起来, 每一层最后一个结点除外
                if(i < size - 1)root.next = queue.peek();

                if(root.left != null)queue.add(root.left);
                if(root.right != null)queue.add(root.right);
            }
        }

        return res;
    }
}

[思路分析二, 递归实现]

/*
// Definition for a Node.
class Node {
    public int val;
    public Node left;
    public Node right;
    public Node next;

    public Node() {}
    
    public Node(int _val) {
        val = _val;
    }

    public Node(int _val, Node _left, Node _right, Node _next) {
        val = _val;
        left = _left;
        right = _right;
        next = _next;
    }
};
*/

class Solution {
    //1. 递归函数: 连接同一层的结点, 参数: 以当前节点为根节点的结点;
    // 返回值:  返回的是被看做根节点的当前节点
    public Node connect(Node root) {
        //2. 递归结束条件
        if(root == null)return root;

        //3. 单层递归逻辑
        if(root.left != null){
            //3.1 连接一棵子树内的左右结点
            root.left.next = root.right;
            //3.2 连接不同子树之间的右结点和左结点
            //上层的next结点已经是已知的, 所以我们利用root.next获取到root右边的那棵子树
            if(root.next != null)root.right.next = root.next.left;
        }
        
		//4. 递归调用
        connect(root.left);
        connect(root.right);


        return root;
    }
}

lt.117. 填充每个节点的下一个右侧节点指针 II

[案例需求]

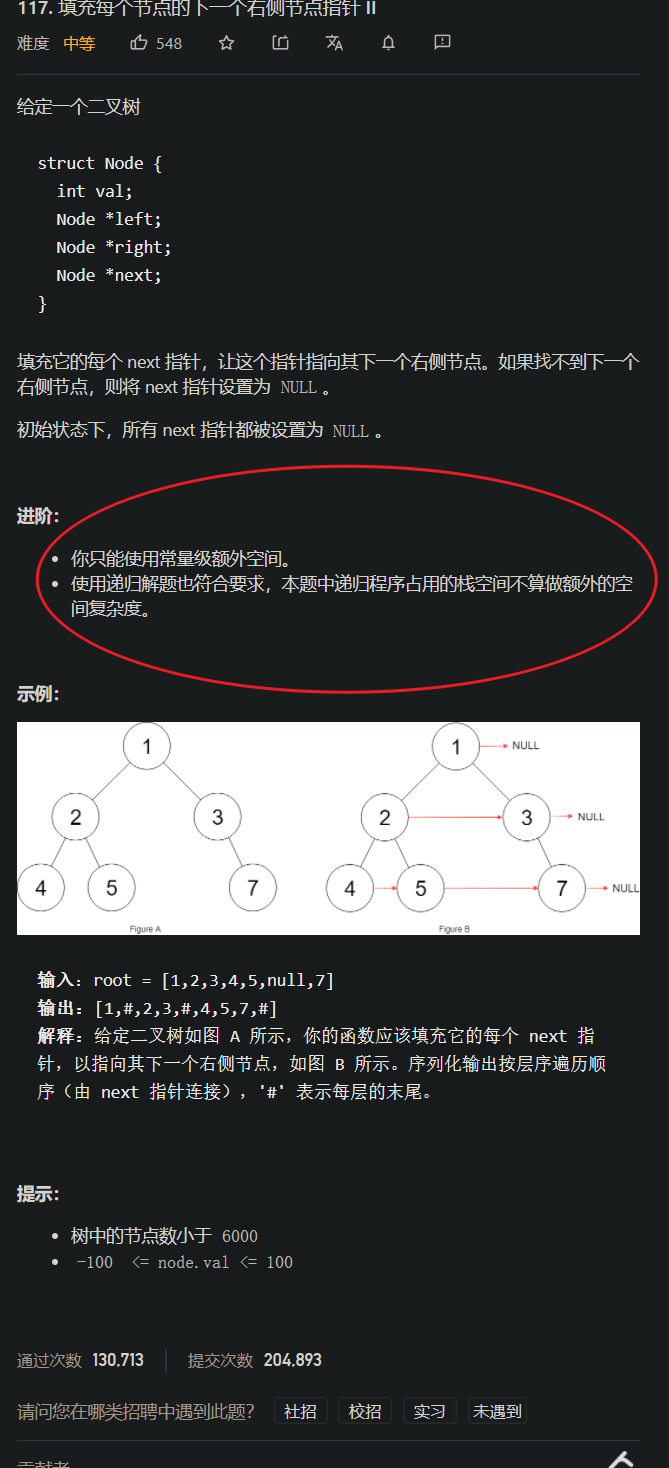
[思路分析一, 借助队列的层序遍历]

• 毋庸多说, 这个解法跟上一题的思路完全一致

[代码实现]

/*
// Definition for a Node.
class Node {
    public int val;
    public Node left;
    public Node right;
    public Node next;

    public Node() {}
    
    public Node(int _val) {
        val = _val;
    }

    public Node(int _val, Node _left, Node _right, Node _next) {
        val = _val;
        left = _left;
        right = _right;
        next = _next;
    }
};
*/

class Solution {
    public Node connect(Node root) {

        if(root == null)return root;

        Queue<Node> queue = new ArrayDeque<>();
        queue.add(root);

        Node res = root;
        while(!queue.isEmpty()){
            int size = queue.size();

            for(int i = 0; i < size; i++){
                root = queue.poll();
                
                if(i < size - 1){
                    root.next = queue.peek();
                }

                 if(root.left != null)queue.add(root.left);
                 if(root.right != null)queue.add(root.right);
            }

        }

        return res;
    }
}

[思路分析二, ]

• 待补充题解: 点我

[代码实现]

/*
// Definition for a Node.
class Node {
    public int val;
    public Node left;
    public Node right;
    public Node next;

    public Node() {}
    
    public Node(int _val) {
        val = _val;
    }

    public Node(int _val, Node _left, Node _right, Node _next) {
        val = _val;
        left = _left;
        right = _right;
        next = _next;
    }
};
*/

class Solution {
    public Node connect(Node root) {
        if (root == null)
            return root;
        //cur我们可以把它看做是每一层的链表
        Node cur = root;
        Node dummy = new Node(0);
        while (cur != null) {
            dummy.next = null;
            //遍历当前层的时候，为了方便操作在下一
            //层前面添加一个哑结点（注意这里是访问
            //当前层的节点，然后把下一层的节点串起来）
            //pre表示访下一层节点的前一个节点
            Node pre = dummy;
            //然后开始遍历当前层的链表
            while (cur != null) {
                if (cur.left != null) {
                    //如果当前节点的左子节点不为空，就让pre节点
                    //的next指向他，也就是把它串起来
                    pre.next = cur.left;
                    //然后再更新pre
                    pre = pre.next;
                }
                //同理参照左子树
                if (cur.right != null) {
                    pre.next = cur.right;
                    pre = pre.next;
                }
                //继续访问这样行的下一个节点
                cur = cur.next;
            }
            //把下一层串联成一个链表之后，让他赋值给cur，
            //后续继续循环，直到cur为空为止
            cur = dummy.next;
        }
        return root;
    }
}