9.＜tag-二叉树和树的构建＞lt.654. 最大二叉树 + lt.105. 从前序与中序遍历序列构造二叉树(同剑指.07) + lt.106. 从中序与后序遍历序列构造二叉树 dbc

X.＜tag-数组和二分查找＞-lt.xx-xxxxxx + lt.xx-xxxxxx

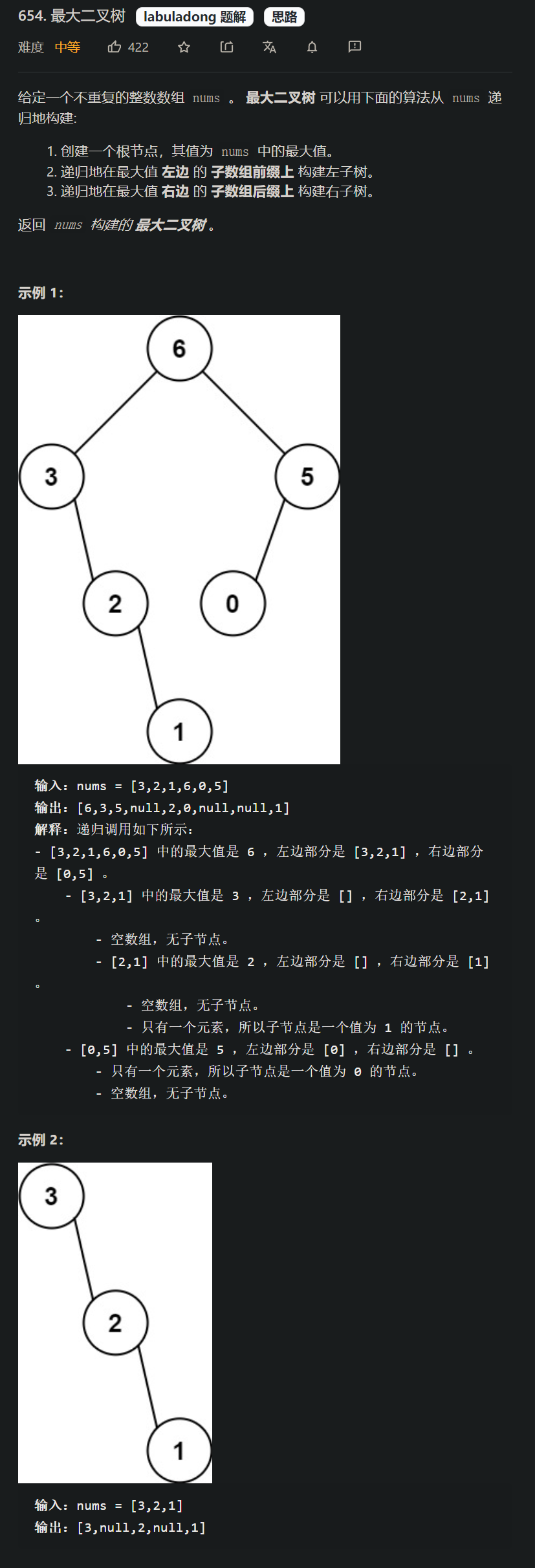
lt.654. 最大二叉树

[案例需求]

[思路分析]

• 本题的大致逻辑是: 从一个数组中找出一个最大的数作为根节点, 然后这个数的左边的数用来构建左子树, 右边的数用来构建右子树.
• 接着往下就是在左子树的范围内找出这个左子树的数组范围内最大的数作为这课左子树的根节点, 右子树也是如此操作, 一个子树的单层递归逻辑就是如此,
• 其他的咱们也不用管了, 直接递归调用就完事了.

[代码实现]

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    //1. 递归函数, 参数树的所有节点, 
    public TreeNode constructMaximumBinaryTree(int[] nums) {
        return construct(nums, 0, nums.length);
    }

    public TreeNode construct(int[] nums, int left, int right){
        //递归结束条件
        if(left == right)return null;

        //单层递归逻辑
        int max_i = findMax(nums, left, right);

        TreeNode root = new TreeNode(nums[max_i]);

        root.left = construct(nums, left, max_i);
        root.right = construct(nums, max_i + 1, right);

        return root;
    }

    //找出一个数组区间内最大的节点作为根节点
    public int findMax(int[] nums, int left, int right){
        int max_i = left;

        for(int i = left; i < right; i++){
            if(nums[max_i] < nums[i]){
                max_i = i;
            }
        }   
        return max_i;
    }
}

lt.105. 从前序与中序遍历序列构造二叉树

[案例需求]

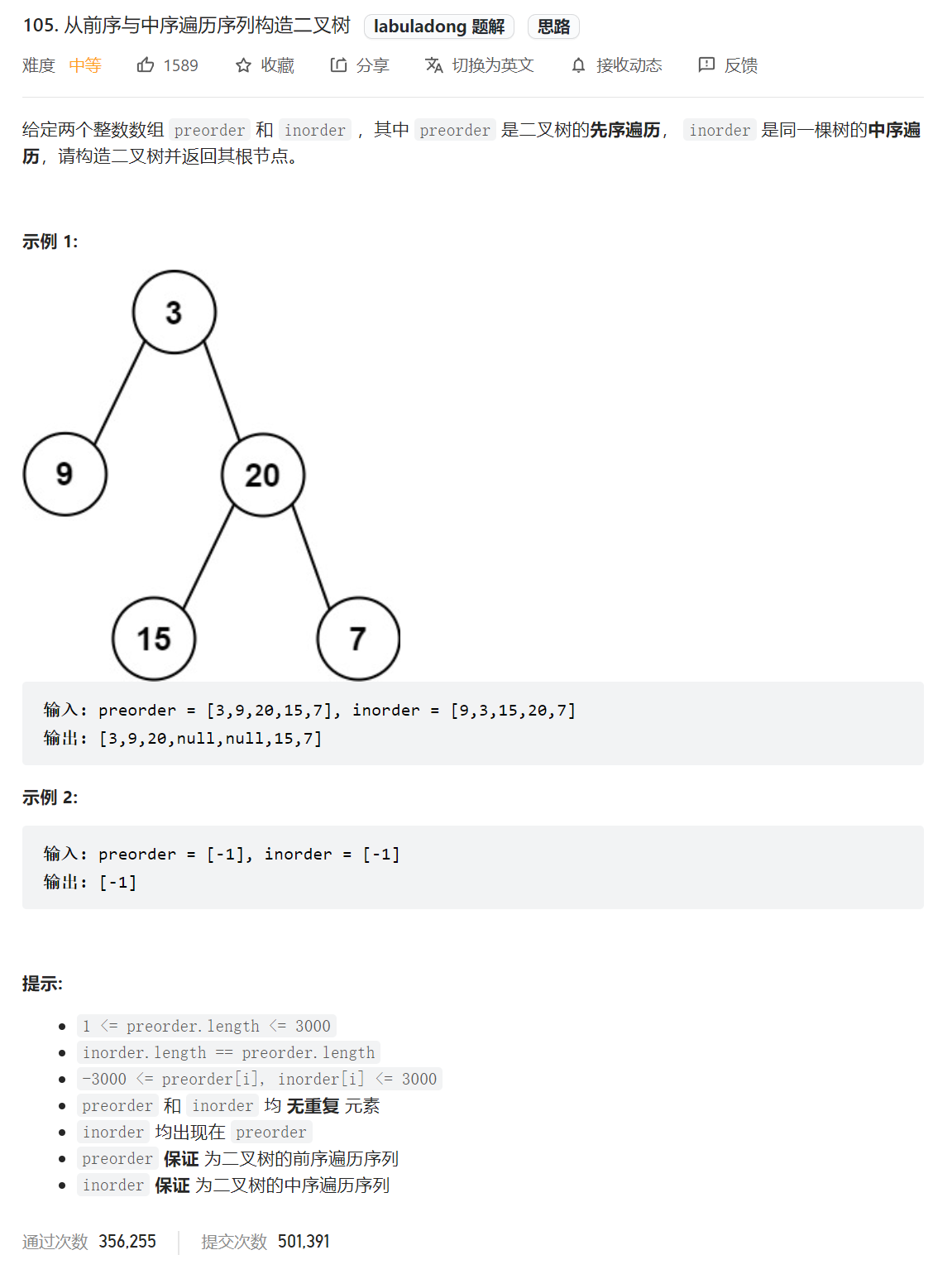
[思路分析]

视频题解: 点我

[代码实现]

• 对递归函数的补充说明:
  

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        int preLen = preorder.length;
        int inLen = inorder.length;

        if(preLen != inLen){
            throw new RuntimeException("error");
        }
        //使用哈希表存储中序遍历的节点和index, 
        //这是为了从前序遍历的到根节点能够很快的在中序遍历序列被定位到位置
        Map<Integer, Integer> map = new HashMap<>();
        for(int i = 0; i < inLen; i++){
            map.put(inorder[i], i);
        }

        return build(preorder, 0, preLen - 1, map, 0, inLen - 1);
    }

    //构建子树的递归方法
    // 构建一棵子树的过程是什么?
    //先得到这课子树的根节点(从前序遍历中得到), 然后在中序遍历序列中得到这个根节点的位置,
    // 得到位置是为了获取到这个根节点的左子节点和右子节点的位置,
    // 把这课子树的根节点和他的左右子树节点连接起来即可.

    //1. 递归函数, 获取到一个节点, 这个节点是被看做根节点的当前节点
    public TreeNode build(int[] preorder, int preLeft, int preRight, 
                Map<Integer, Integer> map, int inLeft, int inRight){
        //2. 递归出口
        if(preLeft > preRight ||inLeft > inRight)return null;

        //3.单层递归逻辑
        // 获取当前节点, 这个节点是根节点(从前序遍历中顺序取到的)
        int rootVal = preorder[preLeft];
        TreeNode root = new TreeNode(rootVal);
        int pIndex = map.get(root.val); //从map中获取这个当前节点在中序遍历中的位置
    
        //连接当前节点的左右孩子节点
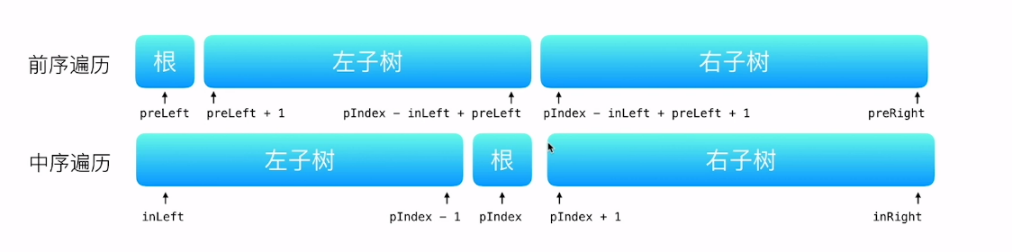
        root.left = build(preorder, preLeft + 1, pIndex - inLeft + preLeft, map, inLeft, pIndex - 1);
        root.right = build(preorder, pIndex - inLeft + preLeft + 1, preRight, map, pIndex + 1, preRight);

        return root;  //单层逻辑完事之后, 返回的是被看做是根节点的当前节点
    }
}

lt.106. 从中序与后序遍历序列构造二叉树

[案例需求]

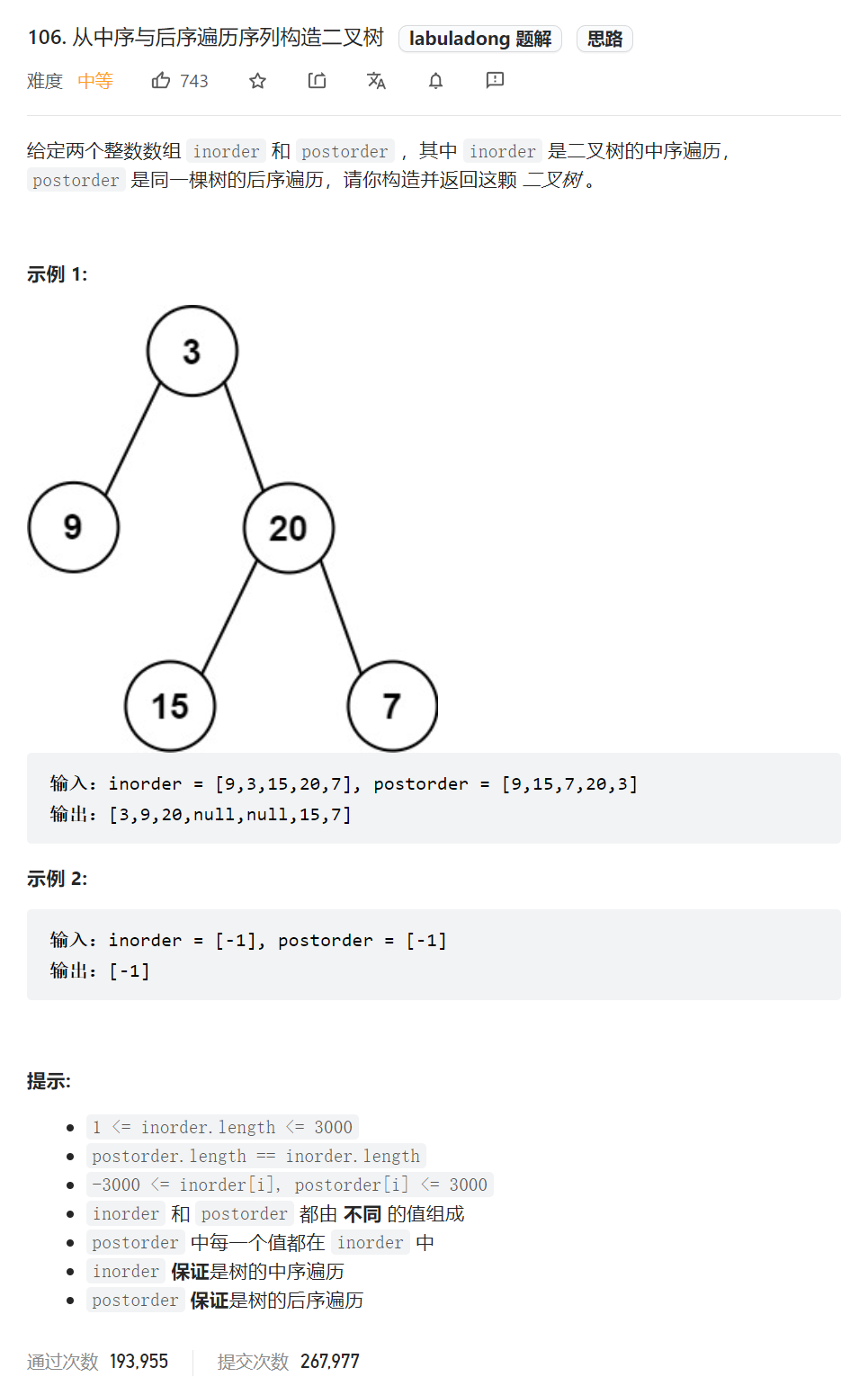
[思路分析]

[代码实现]