学习式轨迹相似性度量(TSM)方法捕捉轨迹时间特征操作对比分析
一、At2vec
3.2 轨迹特征提取(Trajectory feature extraction)
2) 时间信息嵌入编码(Temporal information embedding)
原始表示形式:时间戳
处理方式:用偶数时间间隔将时间戳离散,然后得到一个P序列
预训练方法:the skip-gram 模型来学习每个时间戳的嵌入表示
嵌入表示形式: 通过the skip-gram 模型得到e(P,t)为轨迹Ti中第t个时间戳的嵌入向量。
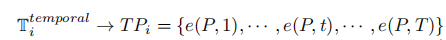
处理本质:使用 Skip-gram 模型来学习轨迹数据中的离散化时间戳信息,实质上是在捕捉时间的上下文信息,即时间序列性。
二、RSTS
1. Introduction
(1) 良好的相似度度量不仅保证了处理低质量轨迹时的鲁棒性,而且实现了较高的效率。前人工作:基于t2vec的轨迹相似性度量方法,虽然考虑了模型的鲁棒性和有效性,但是t2vec模型忽略了轨迹的时间信息。通过考虑时间维度,可以开发更多样的应用,如交通拥塞预测[8]、动物迁移模式挖掘以及热门路径识别[9]。因此,考虑时间信息进行相似度度量是非常重要的。
(2) 传统基于RNNs的编解码模型主要是针对自然语言处理中的文本数据设计的。其特点是含噪声(如拼写错误)很少,并且没有考虑时间信息。若直接应用将有三点局限性:首先,模型输入为离散标记序列,轨迹由采样点表示。其次,在原始编码器-解码器模型中学习到的向量不能简单地再现轨迹的精确运动路径,特别是当轨迹质量较低时。第三,因为最初是为自然语言处理[17]而设计的,所以编码器-解码器模型中使用的原始损失函数无法识别轨迹的时空特征。
(3) 具体实现:RSTS模型通过将空间和时间维度划分为单元,将每个轨迹转换为一系列标记序列。它的训练与一个时空感知损失函数,结合了三重损失。当我们解码一个目标细胞时,时空感知损失函数有利于解码器为目标细胞的最近的时空邻居分配更高的概率。通过使用大量的历史轨迹作为输入进行训练,可以简单地学习隐藏的变换模式。特别是,隐藏的时空特征和变换模式可以通过学习到的轨迹表示来再现。
2. Related work
(1) 传统轨迹相似性度量(Traditional trajectory similarity measure)
(2) 基于深度学习的轨迹相似性度量 (Deep learning based trajectory similarity measure)
(3) 基于道路网络的轨迹相似性度量 (Road matching based trajectory similarity measure)
应用了一些地图匹配算法[51–54]对道路网络上的轨迹进行了对齐。通过地图匹配操作,将轨迹转换为路段序列。基于两个轨迹之间最长的共同路段,建立了轨迹相似度。然而,道路地图并没有考虑到时间方面的问题。两个轨迹穿越相同的区域,但在不同的时间段内可以转化为相同的路段序列。
然后,分别进行路段表示学习和轨迹表示学习,学习路段嵌入和轨迹嵌入。其中最具代表性的工作之一,[49]提出了一个三阶段框架(TremBR)来学习路段的表示,其目标是捕捉轨迹固有的时空特性,同时将学习过程限制在道路网络的拓扑结构上。然而,TremBR中的“时间信息”被转换为每个转换路段的旅行持续时间,而我们的建议将“时间信息”转换为位置时间戳。因此,我们以完全不同的方式来解释“时间信息”的概念
GTS [44]将空间轨迹相似度学习与道路网络环境相结合,取得了最先进的性能。然而,它忽略了轨迹的时间信息,使得它无法在时间方面测量轨迹的相似性。
3. 编解码器架构(Encoder‑decoder framework)
基于道路匹配的方法可能具有更高的精度,但也需要更多的预处理计算量。我们特别关注轨迹相似度度量的鲁棒性和有效性,而不是准确性。
处理方法:首先,我们将空间划分为相同大小的网格单元(例如,200m×200m)[56]。接下来,我们根据特定的时间切片计数将每个空间单元划分为不同数量的时空单元。具体地说,我们将时间维度分割成大量的时间片(例如,500个)。因此,一个轨迹的每个数据点=([x,y],t)都可以用一个特定的标记来表示。然后得到一个轨迹标记序列。【双层切片,空间->时间】
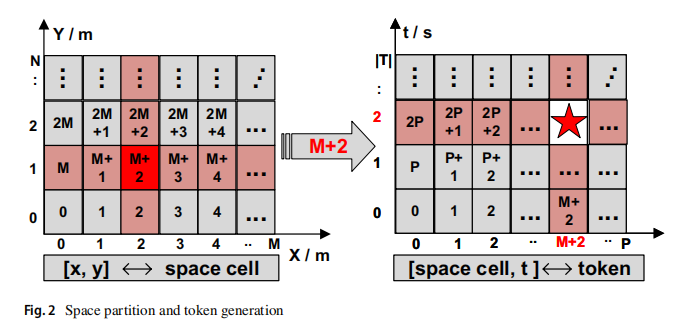
三、GTS+
6.2 时间感知图构造(Temporal-aware Graph Construction)
它需要首先学习每个POI的时间嵌入,然后将其与POI嵌入相结合,以学习整个轨迹的表示。
① 轨迹时间戳表示
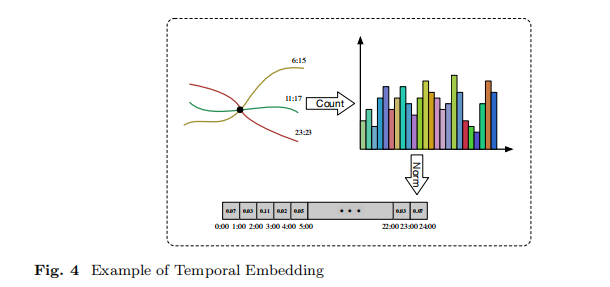
第一步:识别所有poi的时间嵌入。为了达到这一目标,我们首先根据每个POI在轨迹中出现的时间为它建立一个直方图向量。(两个直方图向量越近,两个poi在时间方面就越相似。第二步:构建这样一个直方图: 1)是将整个时间范围划分为一个固定数量的插槽。具体来说,有24个槽,每个槽对应一天1小时的时间范围。一个POI的时间直方图变成一个24维向量。2) 我们遍历轨迹集合,构建所有POI的直方图:对于轨迹上的每个POI,我们根据其相关的时间戳,增加直方图中相应维数的值。)
第三步:将直方图向量标准化,将每个维度的值替换为所有时间范围中的出现百分比,其中所有维度的值之和等于1。这个过程的图表如图4所示。
② 时间感知图构造
基于上述所有poi的时间直方图构造了时间感知图。在第4节中从POI嵌入学习轨迹表示的方法中,我们通过考虑空间网络的结构来构造相邻图G,并学习GNN的嵌入,以解决大搜索空间带来的数据稀疏性问题。沿着这条路径,我们构造了具有时间感知能力的相邻图。
核心构建【比如从时间方面来识别每个POI的邻居。由于POI的时间直方图是一个固定长度的向量,因此两个POI之间的相似度可以计算为它们的直方图向量之间的余弦相似度。然后对于每个POI v,我们在时间方面与它的top-K相似度POI之间添加一条边来构造边集ET。变量K可以看作是一个超参数,我们在本工作中根据经验将其设为20。】GT = ⟨V, ET ⟩
③ 学习轨迹表示
为了构建图GS和GT,我们需要分别基于两个图中的边构造相邻的矩阵MS和MT。在联合训练框架中,我们只构造了一个图G和相邻矩阵M = MS⊙MT的图G,其中⊙是元素级乘积的运算。然后,我们训练一个GNN模型来学习使用相同的方式对每个基于G的POI的嵌入。通过这种方式,GNN模型学习到的POI嵌入已经同时携带了空间和时间信息。最后,我们简单地将轨迹上的poi输入到如图2所示的原始LSTM模型中,以学习轨迹表示。
-------------------------------------------------------------------------------------------------
归纳:1)为每一个POI顶点定义一个直方图(24维,1小时间隔)
2)遍历轨迹数据集中所有轨迹
例如,有3条轨迹经过同一个POI顶点,
T1经过该POI顶点的时间戳为早上6:15、
T2经过该POI顶点的时间戳为中午11:17、
T3经过该POI顶点的时间戳为晚上23:23
因此,该POI顶点对应的第7维、第12维、第24维数值分别加1
3)最终每个POI顶点均获得一个时间直方图向量。
4)由于直方图具有固定向量维度,所以可以通过计算POI顶点的直方图向量的余弦相似度来约等于POI顶点间的相似度。
5)随后,通过top-k来获取POI顶点的相邻顶点,k=20(经验,超参数),相邻POI顶点用边连接,构成边集ET。
6)最终时间感知图GT=<VT, ET> 空间感知图GS=<VS,ES> VT~VS
四、ST2Vec
5.1.1 时间嵌入 Time Embedding.
受BERT [28]中位置嵌入的启发,对于一个时间轨迹中的每个时间点𝑡,我们学习了它的时间嵌入𝑡‘,这是一个大小为𝑞+1的向量。
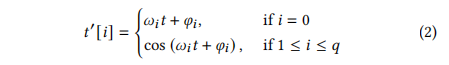

作为一个周期激活函数,帮助捕获周期行为,而不需要特征工程。
对于1≤𝑖≤𝑞,𝜔𝑖和𝜑𝑖是cos函数的频率和相移,因此余弦函数的周期是2𝜋𝜔𝑖,即在𝑡和𝑡+2𝜋𝜔𝑖处具有相同的值。
线性项表示时间的发展,可用于捕获依赖于时间的输入中的非周期模式。
基于等式的2、我们将一个时间轨迹𝑇(𝑡)嵌入到一个时间向量序列中,即𝑡1,𝑡2,...,𝑡𝑚→𝑡‘1,𝑡’2,...,𝑡‘𝑚
5.1.2 时间序列嵌入(Temporal Sequence Embedding)
如果我们去除时空共注意融合模块,在将每个时间点嵌入一个轨迹后,我们可以将𝑡‘1,𝑡’2,...,𝑡‘𝑚输入一个LSTM体系结构来模拟其时间依赖性。LSTM的循环步骤如下。在每个步骤𝑖中,LSTM单元以当前输入向量𝑥𝑖和前一步ℎ𝑖−1的状态向量作为输入,并输出当前步骤ℎ𝑖的状态向量。最后,我们使用最后一个隐藏状态向量ℎ𝑡作为深度时间表示,因为它包含了轨迹的所有时间信息。总的来说,时间信息保存表示是通过处理时间点并捕获时间点之间的相关性的循环过程来学习的。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号