[剑指Offer]65~68

[剑指Offer]65~68

学习使用工具

剑指Offer http://itmyhome.com/sword-means-offer/sword-means-offer.pdf

LeetCode的剑指Offer题库 https://leetcode.cn/problemset/all/

剑指 Offer 65. 不用加减乘除做加法

写一个函数，求两个整数之和，要求在函数体内不得使用 “+”、“-”、“*”、“/” 四则运算符号。

示例:

输入: a = 1, b = 1
输出: 2

提示：

• a, b 均可能是负数或 0
• 结果不会溢出 32 位整数

解法：

第一反应：位运算 第二反应：我不会位运算

def add(self, a: int, b: int) -> int:
        return sum([a,b])

贴一下位运算的解法，a^b 是无进制相加 a&b是进位信息

MASK1 = 4294967296  # 2^32
MASK2 = 2147483648  # 2^31
MASK3 = 2147483647  # 2^31-1

class Solution:
    def add(self, a: int, b: int) -> int:
        a %= MASK1
        b %= MASK1
        while b != 0:
            carry = ((a & b) << 1) % MASK1
            a = (a ^ b) % MASK1
            b = carry
        if a & MASK2:  # 负数
            return ~((a ^ MASK2) ^ MASK3)
        else:  # 正数
            return a

剑指 Offer 66. 构建乘积数组

给定一个数组 A[0,1,…,n-1]，请构建一个数组 B[0,1,…,n-1]，其中 B[i] 的值是数组 A 中除了下标 i 以外的元素的积, 即 B[i]=A[0]×A[1]×…×A[i-1]×A[i+1]×…×A[n-1]。不能使用除法。

示例:

输入: [1,2,3,4,5]
输出: [120,60,40,30,24]

提示：

• 所有元素乘积之和不会溢出 32 位整数
• a.length <= 100000

解法：

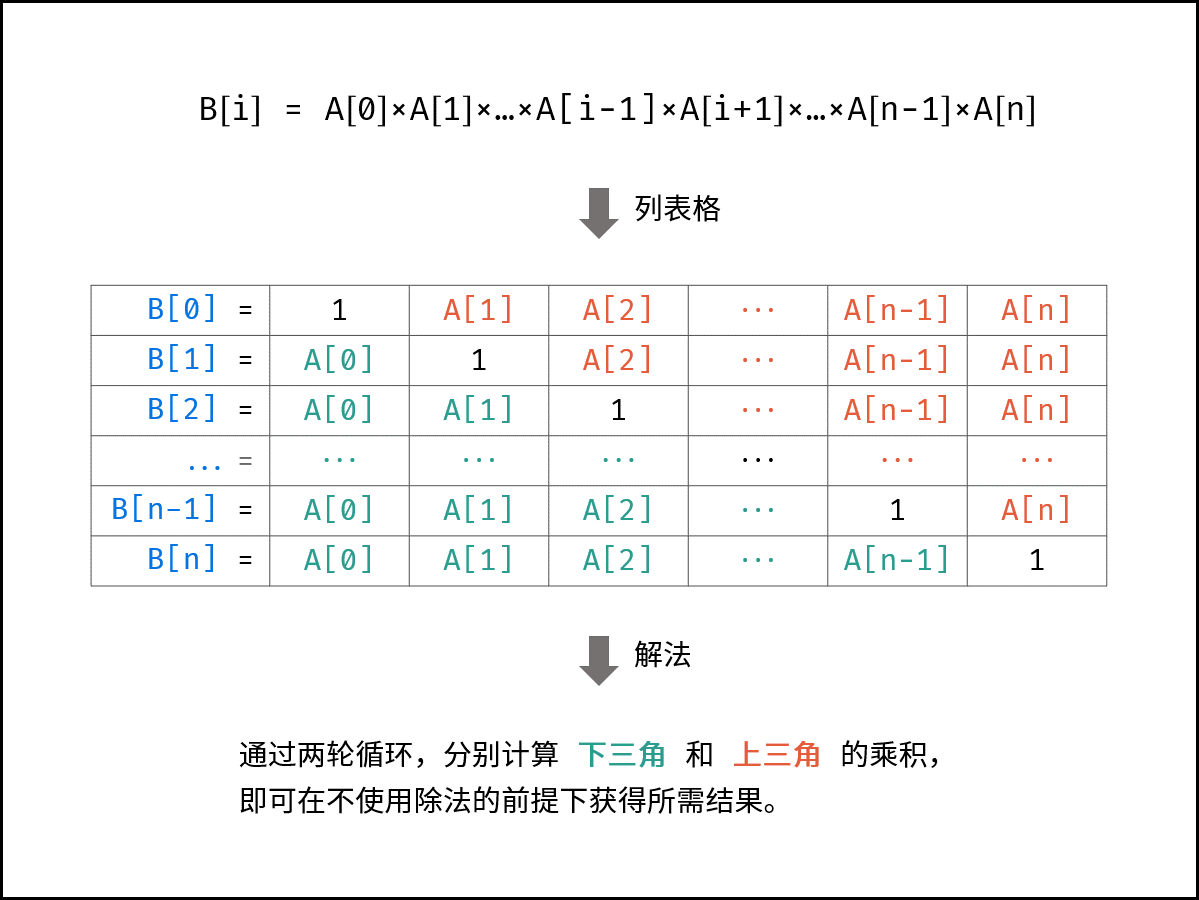
def constructArr(self, a: List[int]) -> List[int]:
        b = [1] * len(a)
        tmp = 1

        for i in range(1, len(a)):
            b[i] = b[i - 1] * a[i - 1]
        
        for i in range(len(a) - 2, -1, -1):
            tmp *= a[i + 1]
            b[i] *= tmp
        
        return b

剑指 Offer 68 - I. 二叉搜索树的最近公共祖先

给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

例如，给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]

示例 1:

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6 
解释: 节点 2 和节点 8 的最近公共祖先是 6。

示例 2:

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。

说明:

• 所有节点的值都是唯一的。

• p、q 为不同节点且均存在于给定的二叉搜索树中。

  ​

解法：

遍历到第一个使待查找两个节点在左右两边时，返回该节点；如果待查找两个节点都比当前节点大，返回右子树的遍历结果，否则返回左子树的遍历结果。

def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
        if not root:
            return None
        if root.val >= p.val and root.val <= q.val:
            return root
        elif root.val <= p.val and root.val >= q.val:
            return root

        if root.val <= p.val:
            return self.lowestCommonAncestor(root.right, p, q)
        else:
            return self.lowestCommonAncestor(root.left, p, q)

剑指 Offer 68 - II. 二叉树的最近公共祖先

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

例如，给定如下二叉树: root = [3,5,1,6,2,0,8,null,null,7,4]

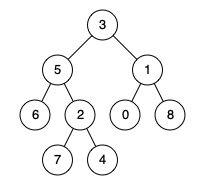
示例 1:

输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出: 3
解释: 节点 5 和节点 1 的最近公共祖先是节点 3。

示例 2:

输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出: 5
解释: 节点 5 和节点 4 的最近公共祖先是节点 5。因为根据定义最近公共祖先节点可以为节点本身。

说明:

• 所有节点的值都是唯一的。
• p、q 为不同节点且均存在于给定的二叉树中。

解法：

先写了个递归，然后超时了……

class Solution:
    def find(self, root, target):
        if not root:
            return False
        
        if root == target:
            return True
        else:
            return self.find(root.left, target) or self.find(root.right, target)

    def lowestCommonAncestor(self, root: TreeNode, p: TreeNode, q: TreeNode) -> TreeNode:
        if not root:
            return None

        l = self.find(root.left, p)
        r = self.find(root.right, q)

        if (l or root == p) and (r or root == q):
            return root
        elif (not l or root == p) and (not r or root == q):
            return root

        if l:
            return self.lowestCommonAncestor(root.left, p, q)
        else:
            return self.lowestCommonAncestor(root.right, p, q)

优化了一下递归代码，通过了。

def lowestCommonAncestor(self, root: TreeNode, p: TreeNode, q: TreeNode) -> TreeNode:
        if not root:
            return None

        if root == p or root == q:
            return root

        l = self.lowestCommonAncestor(root.left, p, q)
        r = self.lowestCommonAncestor(root.right, p, q)

        if l and r:
            return root
        if l:
            return l
        else:
            return r