[LeetCode 热题 HOT 100]1、2、3、4

[LeetCode 热题 HOT 100]1、2、3、4

学习使用工具

🔥 LeetCode 热题 HOT 100 https://leetcode.cn/problem-list/2cktkvj/?page=1

1.两数之和

给定一个整数数组 nums 和一个整数目标值 target，请你在该数组中找出 **和为目标值 ** target 的那 两个 整数，并返回它们的数组下标。

你可以假设每种输入只会对应一个答案。但是，数组中同一个元素在答案里不能重复出现。

你可以按任意顺序返回答案。

示例 1：

输入：nums = [2,7,11,15], target = 9
输出：[0,1]
解释：因为 nums[0] + nums[1] == 9 ，返回 [0, 1] 。

示例 2：

输入：nums = [3,2,4], target = 6
输出：[1,2]

示例 3：

输入：nums = [3,3], target = 6
输出：[0,1]

提示：

• 2 <= nums.length <= 104
• -109 <= nums[i] <= 109
• -109 <= target <= 109
• 只会存在一个有效答案

进阶：你可以想出一个时间复杂度小于 O(n^2) 的算法吗？

解法：

暴搜，暴搜！

def twoSum(self, nums: List[int], target: int) -> List[int]:
        n = len(nums)
        for i in range(n):
            for j in range(i + 1, n):
                if nums[i] + nums[j] == target:
                    return [i, j]
        
        return []

先排序再用双指针可以将时间复杂度降低到O(NlogN)，开辟一个temp数组用来记录原数组的下标位置的变化。

def twoSum(self, nums: List[int], target: int) -> List[int]:
        temp = [i for i in range(len(nums))]

        def sort(i, j):
            if i >= j :
                return
            key = nums[i]
            tmp = temp[i]
            l = i
            r = j
            while l < r:
                while l < r and nums[r] >= key:
                    r -= 1
                nums[l] = nums[r]
                temp[l] = temp[r]
                while l < r and nums[l] <= key:
                    l += 1
                nums[r] = nums[l]
                temp[r] = temp[l]
            nums[l] = key
            temp[l] = tmp
            
            sort(i, l)
            sort(l + 1, j)
                

        i = 0
        j = len(nums) - 1
        sort(i, j)

        while i <= j:
            if nums[i] + nums[j] < target:
                i += 1
            elif nums[i] + nums[j] > target:
                j -= 1
            else:
                break
        
        return [temp[i], temp[j]]

2. 两数相加

给你两个 非空 的链表，表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的，并且每个节点只能存储 一位 数字。

请你将两个数相加，并以相同形式返回一个表示和的链表。

你可以假设除了数字 0 之外，这两个数都不会以 0 开头。

示例 1：

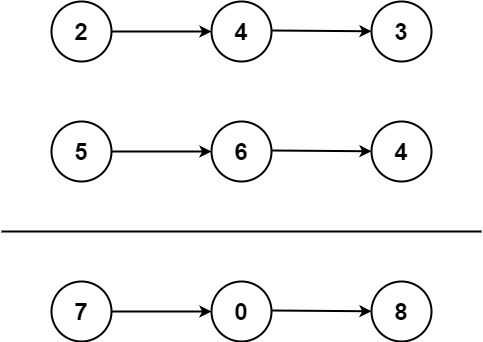
输入：l1 = [2,4,3], l2 = [5,6,4]
输出：[7,0,8]
解释：342 + 465 = 807.

示例 2：

输入：l1 = [0], l2 = [0]
输出：[0]

示例 3：

输入：l1 = [9,9,9,9,9,9,9], l2 = [9,9,9,9]
输出：[8,9,9,9,0,0,0,1]

提示：

• 每个链表中的节点数在范围 [1, 100] 内

• 0 <= Node.val <= 9

• 题目数据保证列表表示的数字不含前导零

  ​

解法：

处理好进位即可。

def addTwoNumbers(self, l1: Optional[ListNode], l2: Optional[ListNode]) -> Optional[ListNode]:
        if not l1:
            return l2
        if not l2:
            return l1

        l1.val += l2.val
        if l1.val >= 10 :
            l1.next = self.addTwoNumbers(l1.next, ListNode(l1.val // 10))
            l1.val %= 10

        l1.next = self.addTwoNumbers(l1.next, l2.next)

        return l1

3.无重复字符的最长子串

给定一个字符串 s ，请你找出其中不含有重复字符的 **最长子串 **的长度。

示例 1:

输入: s = "abcabcbb"
输出: 3 
解释: 因为无重复字符的最长子串是 "abc"，所以其长度为 3。

示例 2:

输入: s = "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b"，所以其长度为 1。

示例 3:

输入: s = "pwwkew"
输出: 3
解释: 因为无重复字符的最长子串是 "wke"，所以其长度为 3。
     请注意，你的答案必须是 子串 的长度，"pwke" 是一个子序列，不是子串。

提示：

• 0 <= s.length <= 5 * 104
• s 由英文字母、数字、符号和空格组成

解法：

剑指做过，滑动窗口即可。

def lengthOfLongestSubstring(self, s: str) -> int:
        gather, r, ans = set(), 0, 0
        
        for l in range(len(s)):
            while r < len(s) and not s[r] in gather:
                gather.add(s[r])
                r += 1
            ans = max(ans, r - l)
            gather.remove(s[l])

        return ans

4. 寻找两个正序数组的中位数

给定两个大小分别为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。

算法的时间复杂度应该为 O(log (m+n)) 。

示例 1：

输入：nums1 = [1,3], nums2 = [2]
输出：2.00000
解释：合并数组 = [1,2,3] ，中位数 2

示例 2：

输入：nums1 = [1,2], nums2 = [3,4]
输出：2.50000
解释：合并数组 = [1,2,3,4] ，中位数 (2 + 3) / 2 = 2.5

提示：

• nums1.length == m
• nums2.length == n
• 0 <= m <= 1000
• 0 <= n <= 1000
• 1 <= m + n <= 2000
• -106 <= nums1[i], nums2[i] <= 106

解法：

说得好，我选择排序加sort。

def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:
        nums1.extend(nums2)
        nums1.sort()

        if not nums1:
            return None
        elif len(nums1) == 1:
            return nums1[0]
        else:
            if len(nums1) % 2 == 0:
                return (nums1[len(nums1) // 2] + nums1[len(nums1) // 2 - 1]) / 2.0
            return nums1[len(nums1) // 2]

时间复杂度带对数的基本都考虑用二分求解。

根据中位数的定义，这道题可以转化成寻找两个有序数组中的第 \(k\) 小的数。

假设两个有序数组分别是 A 和 B。要找到第 k 个元素，我们可以比较 A[k/2−1] 和 B[k/2−1]：

• 如果 \(A[k/2−1]<=B[k/2−1]\)，则比 \(A[k/2−1]\) 小的数最多只有 A 的前 k/2−1 个数和 B 的前 \(k/2−1\) 个数，即比 \(A[k/2−1]\) 小的数最多只有 \(k−2\)个，因此 \(A[k/2−1]\) 不可能是第 \(k\) 个数，\(A[k/2-1]\)以及之前的数都可以全部排除。
• 如果 \(A[k/2−1]>B[k/2−1]\)，则可以排除 \(B[0]\) 到 \(B[k/2−1]\)。

边界条件：

• 如果 \(A[k/2−1]\) 或者 \(B[k/2−1]\) 越界，选取对应数组中的最后一个元素。在这种情况下，根据排除数的个数减少 \(k\) 的值。
• 如果一个数组为空，返回另一个数组中第 k 小的元素。
• 如果 k=1，返回两个数组首元素的最小值。

def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:
        def getKthElement(k):
            index1, index2 = 0, 0
            while True:
                # 特殊情况
                if index1 == m:
                    return nums2[index2 + k - 1]
                if index2 == n:
                    return nums1[index1 + k - 1]
                if k == 1:
                    return min(nums1[index1], nums2[index2])

                # 正常情况
                newIndex1 = min(index1 + k // 2 - 1, m - 1)
                newIndex2 = min(index2 + k // 2 - 1, n - 1)
                pivot1, pivot2 = nums1[newIndex1], nums2[newIndex2]
                if pivot1 <= pivot2:
                    k -= newIndex1 - index1 + 1
                    index1 = newIndex1 + 1
                else:
                    k -= newIndex2 - index2 + 1
                    index2 = newIndex2 + 1
        
        m, n = len(nums1), len(nums2)
        totalLength = m + n
        if totalLength % 2 == 1:
            return getKthElement((totalLength + 1) // 2)
        else:
            return (getKthElement(totalLength // 2) + getKthElement(totalLength // 2 + 1)) / 2