【leetcode】1514. Path with Maximum Probability
题目如下:
You are given an undirected weighted graph of
nnodes (0-indexed), represented by an edge list whereedges[i] = [a, b]is an undirected edge connecting the nodesaandbwith a probability of success of traversing that edgesuccProb[i].Given two nodes
startandend, find the path with the maximum probability of success to go fromstarttoendand return its success probability.If there is no path from
starttoend, return 0. Your answer will be accepted if it differs from the correct answer by at most 1e-5.Example 1:
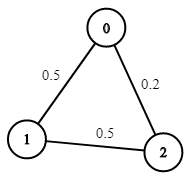
Input: n = 3, edges = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.2], start = 0, end = 2 Output: 0.25000 Explanation: There are two paths from start to end, one having a probability of success = 0.2 and the other has 0.5 * 0.5 = 0.25.Example 2:
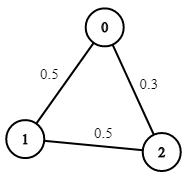
Input: n = 3, edges = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.3], start = 0, end = 2 Output: 0.30000Example 3:
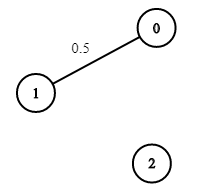
Input: n = 3, edges = [[0,1]], succProb = [0.5], start = 0, end = 2 Output: 0.00000 Explanation: There is no path between 0 and 2.Constraints:
2 <= n <= 10^40 <= start, end < nstart != end0 <= a, b < na != b0 <= succProb.length == edges.length <= 2*10^40 <= succProb[i] <= 1- There is at most one edge between every two nodes.
解题思路:采用BFS的方法,从start开始,依次可以把能到达的节点加入队列中,加入队列之前需要判断通过当前路径到达节点的几率是否比之前其他路径的几率大,只有大于的情况,才能把节点加入队列。
代码如下:
class Solution(object): def maxProbability(self, n, edges, succProb, start, end): """ :type n: int :type edges: List[List[int]] :type succProb: List[float] :type start: int :type end: int :rtype: float """ dic = {} dic_succ = {} for i in range(len(edges)): e1, e2 = edges[i] dic_succ[(e1,e2)] = succProb[i] dic[e1] = dic.setdefault(e1,[]) + [e2] dic[e2] = dic.setdefault(e2,[]) + [e1] max_prob = [0.0] * n max_prob[start] = 1 queue = [start] while len(queue) > 0: node = queue.pop(0) prob = max_prob[node] if node not in dic:continue elif node == end: continue for next_node in dic[node]: edge_prob = dic_succ[(node,next_node)] if (node,next_node) in dic_succ else dic_succ[(next_node,node)] if prob * edge_prob > max_prob[next_node]: max_prob[next_node] = prob * edge_prob queue.append(next_node) return max_prob[end]



 浙公网安备 33010602011771号
浙公网安备 33010602011771号