【leetcode】1210. Minimum Moves to Reach Target with Rotations

题目如下：

In an n*n grid, there is a snake that spans 2 cells and starts moving from the top left corner at (0, 0)and (0, 1). The grid has empty cells represented by zeros and blocked cells represented by ones. The snake wants to reach the lower right corner at (n-1, n-2) and (n-1, n-1).

In one move the snake can:

• Move one cell to the right if there are no blocked cells there. This move keeps the horizontal/vertical position of the snake as it is.
• Move down one cell if there are no blocked cells there. This move keeps the horizontal/vertical position of the snake as it is.
• Rotate clockwise if it's in a horizontal position and the two cells under it are both empty. In that case the snake moves from (r, c) and (r, c+1) to (r, c) and (r+1, c).
  
• Rotate counterclockwise if it's in a vertical position and the two cells to its right are both empty. In that case the snake moves from (r, c) and (r+1, c) to (r, c) and (r, c+1).
  

Return the minimum number of moves to reach the target.

If there is no way to reach the target, return -1.

 

Example 1:

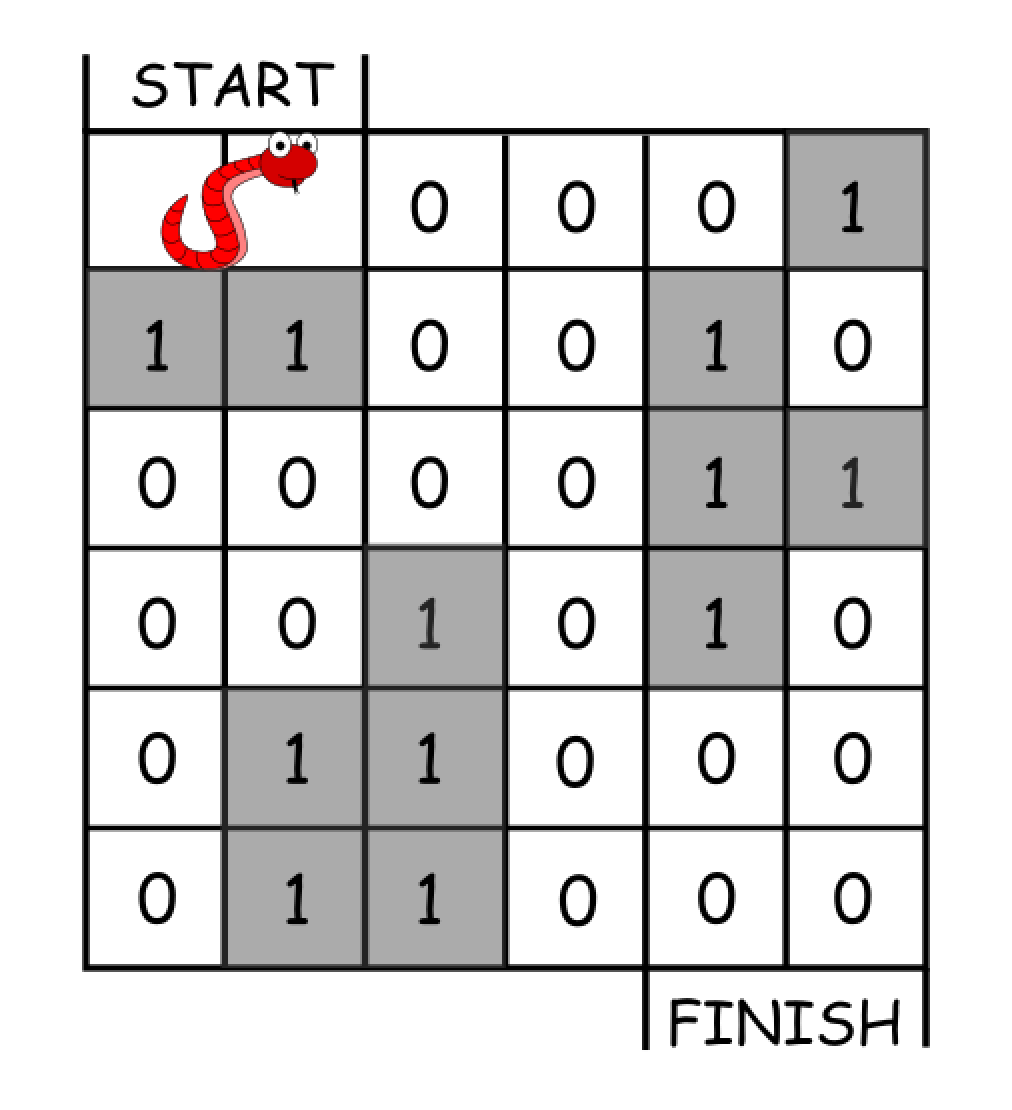
Input: grid = [[0,0,0,0,0,1],
               [1,1,0,0,1,0],
               [0,0,0,0,1,1],
               [0,0,1,0,1,0],
               [0,1,1,0,0,0],
               [0,1,1,0,0,0]]
Output: 11
Explanation:
One possible solution is [right, right, rotate clockwise, right, down, down, down, down, rotate counterclockwise, right, down].

Example 2:

Input: grid = [[0,0,1,1,1,1],
               [0,0,0,0,1,1],
               [1,1,0,0,0,1],
               [1,1,1,0,0,1],
               [1,1,1,0,0,1],
               [1,1,1,0,0,0]]
Output: 9

 

Constraints:

• 2 <= n <= 100
• 0 <= grid[i][j] <= 1
• It is guaranteed that the snake starts at empty cells.

解题思路：典型的BFS题目。特别要注意的是蛇在水平/垂直方向是可以平移的。比如当前所在的左边是(0,0)(0,1)，可以平移到(1,0),(1,1)。

代码如下：

class Solution(object):
    def minimumMoves(self, grid):
        """
        :type grid: List[List[int]]
        :rtype: int
        """
        res = float('inf')
        queue = [(0,0,0,1,0)]
        dic = {}
        dic[(0,0,0,1)] = 0
        while len(queue) > 0:
            tx,ty,hx,hy,count = queue.pop(0)
            #print tx,ty,hx,hy,count
            if hx == len(grid) - 1 == hy and tx == len(grid)-1 and ty == len(grid) - 2:
                res = min(res,count)
                continue
            if tx == hx and ty < hy: #head to right
                if hy + 1 < len(grid) and grid[hx][hy+1] == 0:
                    key = (tx,ty+1,hx,hy+1)
                    if key not in dic or dic[key] > count + 1:
                        queue.append((tx,ty+1,hx,hy+1,count+1))
                        dic[key] = count + 1
                if hx + 1 < len(grid) and grid[tx+1][ty] == 0 and grid[hx+1][hy] == 0:
                    key = (tx, ty, hx+1, ty)
                    if key not in dic or dic[key] > count + 1:
                        queue.append((tx, ty, hx+1, ty, count + 1))
                        dic[key] = count + 1
                    key = (tx+1,ty,hx+1,hy)
                    if key not in dic or dic[key] > count + 1:
                        queue.append((tx+1,ty,hx+1,hy, count + 1))
                        dic[key] = count + 1
            elif tx < hx and ty == hy: #head to down
                if hx + 1 < len(grid) and grid[hx+1][hy] == 0:
                    key = (tx+1,ty,hx+1,hy)
                    if key not in dic or dic[key] > count + 1:
                        queue.append((tx+1,ty,hx+1,hy,count+1))
                        dic[key] = count + 1
                if hy + 1 < len(grid) and grid[hx][hy+1] == 0 and grid[tx][ty+1] == 0:
                    key = tx,ty,tx,ty+1
                    if key not in dic or dic[key] > count + 1:
                        queue.append((tx,ty,tx,ty+1,count+1))
                        dic[key] = count + 1
                    key = tx, ty+1, tx, ty + 1
                    if key not in dic or dic[key] > count + 1:
                        queue.append((tx,ty+1,hx,hy+1,count+1))
                        dic[key] = count + 1
        return res if res != float('inf') else -1