什么是齐次坐标系?为什么要用齐次坐标系?
机器人基础数学知识-什么是齐次坐标系?为什么要用齐次坐标系?
这篇文章内容主要学习自参考链接[1][2]中的内容。如有侵权,请联系删除~~
在了解齐次坐标与非齐次坐标之前,首先了解一下笛卡尔坐标系。
一、笛卡尔坐标系
- 笛卡尔坐标系
笛卡尔坐标系(Cartesian coordinates)就是直角坐标系和斜角坐标系的统称。
相交于原点的两条数轴,构成了平面仿射坐标系。 如两条数轴上的度量单位相等,则称此仿射坐标系为笛卡尔坐标系。
两条数轴互相垂直的笛卡尔坐标系,称为笛卡尔直角坐标系,否则称为笛卡尔斜角坐标系。
笛卡尔直角坐标系就是我们常见的直角坐标系,包括平面直角坐标系、空间直角坐标系。
也就是下图中的关系:

二、什么是齐次(Homogeneous)坐标系?为什么要用齐次坐标系?
这部分内容主要翻译自 http://www.songho.ca/math/homogeneous/homogeneous.html
1. 问题: 两条平行线能相交
在欧氏(几何)空间,同一平面的两条平行线永远不能相交,这是我们都熟悉的一种场景。 然而,在透视空间里面,两条平行线可以相交,例如:火车轨道随着我们的视线越来越窄,最后两条平行线在无穷远处交于一点。

欧氏空间(或者笛卡尔空间)描述2D/3D几何非常适合,但是这种方法却不适合处理透视空间的问题(实际上,欧氏几何是透视几何的一个子集合),2D笛卡尔坐标可以表示为 (𝑥,𝑦) 。
如果一个点在无穷远处,这个点的坐标将会 (∞,∞) ,在欧氏空间中,这就变得没有意义。平行线在透视空间的无穷远处交于一点,但是在欧氏空间却不能表示,数学家发现了一种方式来解决这个问题 (那就是 齐次坐标)。
2. 解决方法:齐次坐标
齐次坐标是由 August Ferdinand Möbius 引入的,使其在投影空间中进行图形和几何计算成为可能。
简而言之,齐次坐标就是用N+1维来代表N维坐标
我们可以在一个2D笛卡尔坐标末尾加上一个额外的变量w来形成 2D齐次坐标。因此,一个在笛卡尔坐标系下的点$(X, Y)$在齐次坐标里面变成了 (𝑥,𝑦,𝑤) ,并且有
𝑋=𝑥/𝑤;
𝑋=𝑥/𝑤;
例如,笛卡尔坐标系下 (1,2) 齐次坐标可以表示为 (1,2,1) ,如果点 (1,2) 移动到无限远处,在笛卡尔坐标下它变为 (∞,∞) ,然后它的齐次坐标表示为 (1,2,0) ,因为 (1/0,2/0)=(∞,∞) 。 注意这样的话,我们可以不用 ” ∞ " 来表示一个无穷远处的点了~~~
3. 为什么叫齐次坐标?
如前面所述,我们把齐次坐标转化为笛卡尔坐标的方法是前面n-1个坐标分量分别除以最后一个分量即可。
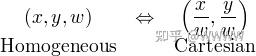
把坐标从齐次坐标转换为笛卡尔坐标,我们可以发现这样一个事实。看下面的例子:

你会发现 (1,2,3) , (4,8,12) 和 (4,8,12) 对应同一个欧几里得点(笛卡尔空间点) (1/3,2/3) 。任何标量的乘积,(1𝑎,2𝑎,3𝑎) 对应 笛卡尔空间里面的都是 (1/3,2/3) 。因此,这些点是“齐次的 (Homogeneous adj. 同类的,同质的)”,因为他们代表了欧氏空间(笛卡尔坐标空间)里面的同一个点。换句话说,齐次坐标有规模不变性。
4. 证明:两条直线可以相交
考虑如下欧几里得空间的线性系统方程:
{𝐴𝑥+𝐵𝑦+𝐶=0𝐴𝑥+𝐵𝑦+𝐷=0
我们知道在笛卡尔坐标系里面,如果𝐶≠𝐷该方程组无解。如果 𝐶=𝐷 ,两条直线就相同了。
在透视空间里中,让我们用齐次坐标 $x/w, y/w$ 分别代替 $x ,y$ 重写这个方程:
{𝐴𝑥𝑤+𝐵𝑦𝑤+𝐶=0𝐴𝑥𝑤+𝐵𝑦𝑤+𝐷=0
可以化为:
{𝐴𝑥+𝐵𝑦+𝐶𝑤=0𝐴𝑥+𝐵𝑦+𝐷𝑤=0
现在我们有一个解 (𝑥,𝑦,0) ,因为 (𝐶−𝐷)𝑤=0 ,所以 𝑤=0 。因此,两条直线相交于 (𝑥,𝑦,0) ,这个点在无穷远处。
齐次坐标是计算机图形学中非常有用的基础概念,比如将3D场景投影到2D平面上。
三、总结
齐次坐标的意义:
如果一个点在无穷远处,这个点的坐标将会 (∞,∞) ,在欧氏空间中,这就变得没有意义。如果使用齐次坐标,平行线在透视空间的无穷远处交于一点,这样就实现了对于无穷点的表示,但是在欧氏空间不能表示无穷点。
也就是说
通过利用齐次坐标就可以表示无穷远处的点。
例如: 笛卡尔坐标系下 (1,2) 齐次坐标可以表示为 (1,2,1) ,如果点 (1,2) 移动到无限远处,在笛卡尔坐标下它变为 (∞,∞) ,然后它的齐次坐标表示为 (1,2,0) ,因为 (1/0,2/0)=(∞,∞) 。 注意这样的话,我们可以不用 ” ∞ " 来表示一个无穷远处的点了~~~
四、参考文献
[1] 百度百科. 笛卡尔坐标系 [EB/OL]. (2021-01-12) [2021-05-20]. https://baike.baidu.com/item/笛卡尔坐标系/4522878?fr=aladdin
[2] Song Ho Ahn. Homogeneous Coordinates [EB/OL]. (2016) [2021-05-20]. http://www.songho.ca/math/homogeneous/homogeneous.html
[3] (参考链接[2]的翻译) JANESTAR. 关于齐次坐标的理解(经典) [EB/OL]. (2015-03-13) [2021-05-20]. https://blog.csdn.net/janestar/




 浙公网安备 33010602011771号
浙公网安备 33010602011771号