矩阵变换在坐标系中的应用

 

念头通达

数学仿真工具 MathLabTool 开发者

来自专栏 · 矩阵

3 人赞同了该文章

​

展开目录

 

前言

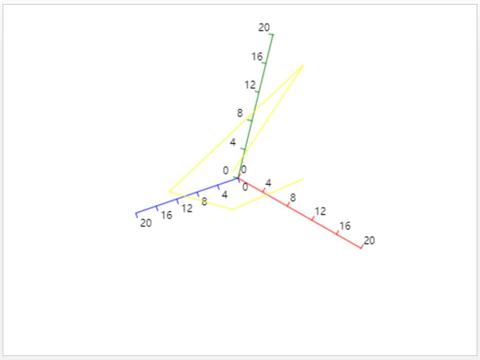
以三维坐标系为例，应用矩阵变换进行坐标平移、缩放、旋转。

原理

对于坐标变换，需要引入齐次坐标的概念。

齐次坐标是将一个原本是n维的向量用一个n+1维向量来表示。

借用F.S. Hill Jr.的一句话来解释为何要引入齐次坐标，“齐次坐标表示是计算机图形学的重要手段之一，它既能够用来明确区分向量和点，同时也更易用于进行仿射（线性）几何变换。”。

其中的几何变换，正是我们需要应用的场景。

这里我们用的是行向量，左乘行变换，右乘列变换。

平移

平移变换的计算，乘一个平移矩阵，可以表示为如下方式：

[𝑥𝑦𝑧1]⋅[100001000010𝑥′𝑦′𝑧′1]=[𝑥+𝑥′𝑦+𝑦′𝑧+𝑧′1]

原坐标(x, y, z)分别平移x', y', z'后，坐标变为(x+x', y+y', z+z')。

缩放（整体）

缩放变换的计算，乘一个缩放矩阵，可以表示为如下方式：

[𝑥𝑦𝑧1]⋅[100001000010000𝑠]=[𝑥𝑠𝑦𝑠𝑧𝑠1]

原坐标(x, y, z)缩放s倍后，坐标变为(x/s, y/s, z/s)。

旋转（绕坐标轴）

旋转变换的计算，乘一个旋转矩阵，x, y, z坐标轴分别表示为：

绕x轴

[𝑥𝑦𝑧1]⋅[10000𝑐𝑜𝑠𝜃𝑠𝑖𝑛𝜃00−𝑠𝑖𝑛𝜃𝑐𝑜𝑠𝜃00001]=[𝑥𝑦⋅𝑐𝑜𝑠𝜃−𝑧⋅𝑠𝑖𝑛𝜃𝑦⋅𝑠𝑖𝑛𝜃+𝑧⋅𝑐𝑜𝑠𝜃1]

绕y轴

[𝑥𝑦𝑧1]⋅[𝑐𝑜𝑠𝜃0−𝑠𝑖𝑛𝜃00100𝑠𝑖𝑛𝜃0𝑐𝑜𝑠𝜃00001]=[𝑥⋅𝑐𝑜𝑠𝜃+𝑧⋅𝑠𝑖𝑛𝜃𝑦𝑧⋅𝑐𝑜𝑠𝜃−𝑥⋅𝑠𝑖𝑛𝜃1]

绕z轴

[𝑥𝑦𝑧1]⋅[𝑐𝑜𝑠𝜃𝑠𝑖𝑛𝜃00−𝑠𝑖𝑛𝜃𝑐𝑜𝑠𝜃0000100001]=[𝑥⋅𝑐𝑜𝑠𝜃−𝑦⋅𝑠𝑖𝑛𝜃𝑦⋅𝑐𝑜𝑠𝜃+𝑥⋅𝑠𝑖𝑛𝜃𝑧1]

仿真

使用MathLabTool进行三维坐标系仿真0 赞同 · 0 评论文章

 

编辑于 2025-02-22 13:55・广东