Lobatto积分类似于Guass积分，但有如下差异：
1. 积分节点包括积分区间的端点.
2. 积分具有2n–3次代数精度，其中n是节点数.
公式如下：
Lobatto quadrature of function f(x) on interval [–1, +1]:
![\int_{-1}^1 {f(x) \, dx} = \frac {2} {n(n-1)}[f(1) + f(-1)] + \sum_{i = 2} ^{n-1} {w_i f(x_i)} + R_n.](http://upload.wikimedia.org/math/c/7/7/c77f8162f24ddb8dddcdd5f2e81da912.png)
Abscissas: 
is
the 
st zero
of 
.
Here Pn(x) are Legendre
polynomials.
Weights:
![w_i = \frac{2}{n(n-1)[P_{n-1}(x_i)]^2} \quad (x_i \ne \pm 1).](http://upload.wikimedia.org/math/d/c/6/dc60d6086449b1dde8c7d5ce3638684f.png)
Remainder: ![R_n = \frac {- n (n-1)^3 2^{2n-1} [(n-2)!]^4} {(2n-1) [(2n-2)!]^3} f^{(2n-2)}(\xi), \quad (-1 < \xi < 1)](http://upload.wikimedia.org/math/9/c/4/9c457ec6355ccc218cfdca0899e342eb.png)
Some of the weights are:
| Number of points, n | Points, xi | Weights, wi |
|---|---|---|
 |
 |
 |
 |
 |
|
 |
 |
 |
|
|
 |
|
 |
|
 |
 |
 |
|
|
|
 |
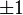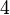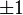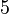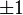摘自：http://en.wikipedia.org/w/index.php?title=Gaussian_quadrature
