[大牛就是牛]双栈排序

【题目描述】

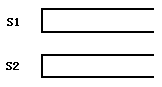
　　Tom最近在研究一个有趣的排序问题。如图所示，通过2个栈S1和S2，Tom希望借助以下4种操作实现将输入序列升序排序。

　　操作a
　　如果输入序列不为空，将第一个元素压入栈S1
　　操作b
　　如果栈S1不为空，将S1栈顶元素弹出至输出序列
　　操作c
　　如果输入序列不为空，将第一个元素压入栈S2
　　操作d
　　如果栈S2不为空，将S2栈顶元素弹出至输出序列

　　如果一个1~n的排列P可以通过一系列操作使得输出序列为1, 2,…,(n-1), n，Tom就称P是一个"可双栈排序排列"。例如(1, 3, 2, 4)就是一个"可双栈排序序列"，而(2, 3, 4, 1)不是。下图描述了一个将(1, 3, 2, 4)排序的操作序列：<a, c, c, b, a, d, d, b>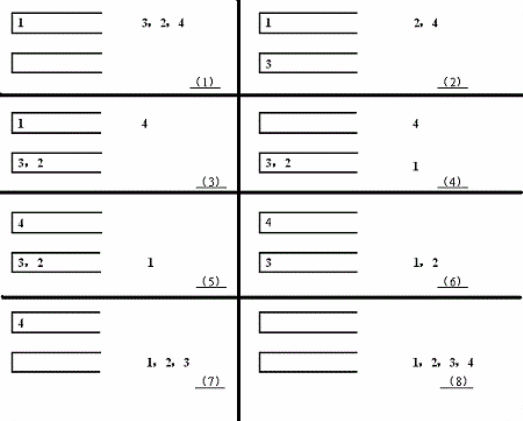

　　当然，这样的操作序列有可能有几个，对于上例(1, 3, 2, 4)，<a, c, c, b, a, d, d, b>是另外一个可行的操作序列。Tom希望知道其中字典序最小的操作序列是什么。

【输入格式】

　　输入的第一行是一个整数n。第二行有n个用空格隔开的正整数，构成一个1~n的排列。

【输出格式】

　　输出共一行，如果输入的排列不是"可双栈排序排列"，输出数字0；否则输出字典序最小的操作序列，每两个操作之间用空格隔开，行尾没有空格。

【输入样例】

3
2 3 1
【输出样例】

a c a b b d
【分析】

　　大家看看SQYBI大牛的题解吧：http://sqybi.com/blog/archives/78

 

#include <stdio.h>
#include <iostream>
#define MAXN 1010
using namespace std;
int a[MAXN],zhan[3][MAXN],color[MAXN],f[MAXN];
int now,n;
bool wujie;
struct tnode {
  int num;
  tnode *next;
} g[MAXN],*t;
void insert(int x,tnode &p) {
  t = new(tnode);
  t->num = x;
  t->next = p.next;
  p.next = t;
}
void dfs(int x) {
  tnode *tt;
  tt = g[x].next;
  while (tt != NULL) {
    int y = tt->num;
    if (!color[y]) {
      color[y] = 3 - color[x];
      dfs(y);
    }
    if (color[y] == color[x]) {
      wujie = 1;
      return;
    }
    tt = tt->next;
  }
}
int main() {

  scanf("%d",&n);
  for (int i = 1;i <= n;++i)
    scanf("%d",&a[i]);
  f[n + 1] = 1000000000;
  for (int i = n;i > 0;--i)
    f[i] = min(a[i],f[i + 1]);
  for (int i = 1;i <= n;++i)
    for (int j = i + 1;j <= n;++j)
      if ((a[i] < a[j]) && (f[j + 1] < a[i])) {
        insert(j,g[i]);
        insert(i,g[j]);
      }
  for (int i = 1;i <= n;++i)
    if (!color[i]) {
      color[i] = 1;
      dfs(i);
      if (wujie)
        break;
    }
  if (wujie) {
    printf("0\n");
    return 0;
  }
  now = 1;
  for (int i = 1;i <= n;++i) {
    int x = color[i];
    zhan[x][++zhan[x][0]] = i;
    if (x == 1)
      printf("a ");
    else
      printf("c ");
    while ((a[zhan[1][zhan[1][0]]] == now) || (a[zhan[2][zhan[2][0]]] == now)) {
      if (a[zhan[1][zhan[1][0]]] == now) {
        printf("b ");
        --zhan[1][0];
      } else {
          printf("d ");
          --zhan[2][0];
        }
      ++now;
    }
  }
}