哈夫曼树
一、定义
哈夫曼树,又称最优树,是一类带权路径长度最短的树。首先有几个概念需要清楚:
1、路径和路径长度
从树中一个结点到另一个结点之间的分支构成两个结点的路径,路径上的分支数目叫做路径长度。树的路径长度是从树根到每一个结点的路径长度之和。
2、带权路径长度
结点的带权路径长度为从该结点到树根之间的路径长度与结点上权的乘积。树的带权路径长度为树中所有叶子结点的带权路径长度之和,通常记作WPL。
若有n个权值为w1,w2,...,wn的结点构成一棵有n个叶子结点的二叉树,则树的带权路径最小的二叉树叫做哈夫曼树或最优二叉树。
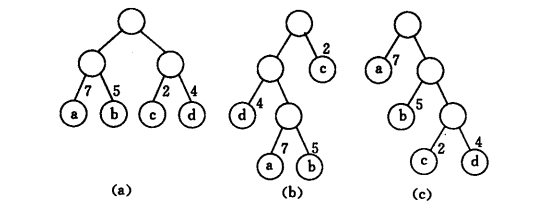
在上图中,3棵二叉树都有4个叶子结点a、b、c、d,分别带权7、5、2、4,则它们的带权路径长度为
(a)WPL = 7*2 + 5*2 + 2*2 + 4*2 = 36
(b)WPL = 4*2 + 7*3 + 5*3 + 2*1 = 46
(c)WPL = 7*1 + 5*2 + 2*3 + 4*3 = 35
其中(c)的WPL最小,可以验证,(c)恰为哈夫曼树。
二、哈夫曼树操作的C++实现
1、结点表示
class Node { public: int val; //结点的值 Node* left; //结点左孩子 Node* right; //结点右孩子 Node* parent; //结点的父结点 Node(int val) :val(val), left(NULL), right(NULL), parent(NULL) {} Node(int val, Node* left, Node* right, Node* parent) :val(val), left(left), right(right), parent(parent) {} };
2、操作
class HuffmanTree { private: priority_queue<Node*, vector<Node*>, Compare> nodes; //优先队列(小根堆) Node* root; public: HuffmanTree(); ~HuffmanTree(); /*创建哈夫曼树,返回根结点*/ Node* create(); /*先序遍历*/ void preOrder(Node* root); /*中序遍历*/ void inOrder(Node* root); /*后序遍历*/ void postOrder(Node* root); /*销毁哈夫曼树*/ void destroyTree(Node* root); };
3、创建哈夫曼树
假设有n个结点,n个结点的权值分别为w1,w2,...,wn,构成的二叉树的集合为F={T1,T2,...,Tn},则可构造一棵含有n个叶子结点的哈夫曼树。步骤如下:
(1)从F中选取两棵根结点权值最小的树作为左右子树构造一棵新的二叉树,其新的二叉树的权值为其左右子树根结点权值之和;
(2)从F中删除上一步选取的两棵二叉树,将新构造的树放到F中;
(3)重复(1)(2),直到F只含一棵树为止。
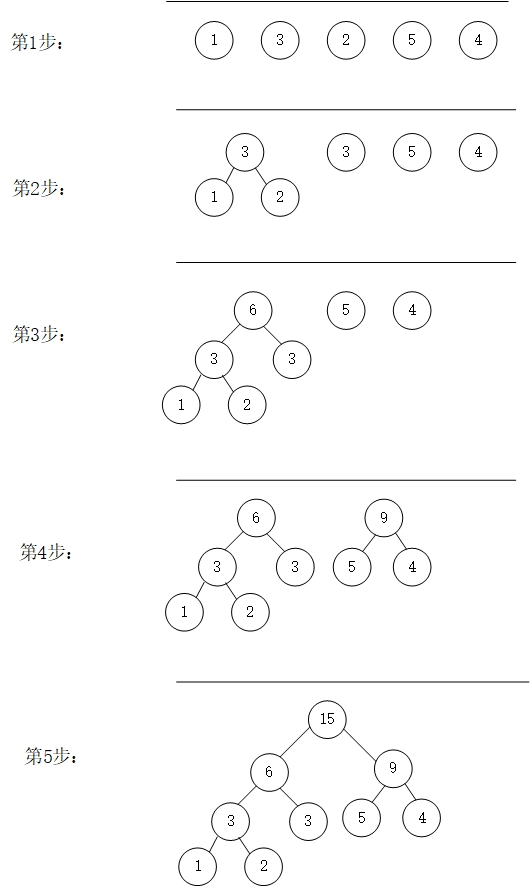
从上面的步骤可以看出,每次选取n个结点中权值最小的两个结点,可以使用小根堆来实现,这里为了简单起见,使用STL中的priority_queue来实现选取权值最小结点的操作。为了保持队列中结点一直按从小到大排序,需要自定义比较函数。由于优先队列中的数据类型为指针类型,所以不能通过重载运算符<来实现,而是要写一个比较类,在构造优先队列时,传入其第3个参数(完整代码中的类Compare)。
4、遍历与删除哈夫曼树
遍历与删除哈夫曼树与遍历和删除普通二叉树没有大的区别,这里只写出代码。
5、哈夫曼树完整代码
1 #include <iostream> 2 #include <queue> 3 using namespace std; 4 5 class Node 6 { 7 public: 8 int val; //结点的值 9 Node* left; //结点左孩子 10 Node* right; //结点右孩子 11 Node* parent; //结点的父结点 12 13 Node(int val) :val(val), left(NULL), right(NULL), parent(NULL) {} 14 Node(int val, Node* left, Node* right, Node* parent) :val(val), left(left), right(right), parent(parent) {} 15 }; 16 17 class Compare //比较类,用于构造Node*类型的priority_queue 18 { 19 public: 20 bool operator() (Node* a, Node* b) 21 { 22 return a->val > b->val; //结点的值越小越靠前 23 } 24 }; 25 26 class HuffmanTree 27 { 28 private: 29 priority_queue<Node*, vector<Node*>, Compare> nodes; //优先队列(小根堆) 30 Node* root; 31 public: 32 HuffmanTree(); 33 ~HuffmanTree(); 34 35 /*创建哈夫曼树,返回根结点*/ 36 Node* create(); 37 38 /*先序遍历*/ 39 void preOrder(Node* root); 40 41 /*中序遍历*/ 42 void inOrder(Node* root); 43 44 /*后序遍历*/ 45 void postOrder(Node* root); 46 47 /*销毁哈夫曼树*/ 48 void destroyTree(Node* root); 49 }; 50 51 HuffmanTree::HuffmanTree() 52 { 53 while (!nodes.empty()) nodes.pop(); 54 int a[] = { 4,3,5,1,2 }; 55 int len = sizeof(a) / sizeof(a[0]); 56 for (int i = 0;i < len; i++) //使用数组的值初始化结点 57 nodes.push(new Node(a[i])); 58 59 root = NULL; 60 } 61 62 HuffmanTree::~HuffmanTree() 63 { 64 destroyTree(root); 65 } 66 67 Node* HuffmanTree::create() 68 { 69 while (nodes.size() > 1) 70 { 71 Node* node1 = nodes.top(); //选取结点值最小的两个结点 72 nodes.pop(); 73 Node* node2 = nodes.top(); 74 nodes.pop(); 75 76 Node* root = new Node(node1->val + node2->val); //新结点的值为两个结点值之和 77 root->left = node1; //将新结点设为两结点的根结点 78 root->right = node2; 79 node1->parent = root; 80 node2->parent = root; 81 nodes.push(root); 82 } 83 84 root = nodes.top(); //队列中最后一个结点即为哈夫曼树的根结点 85 nodes.pop(); 86 87 return root; 88 } 89 90 /*先序遍历*/ 91 void HuffmanTree::preOrder(Node* root) 92 { 93 if (root == NULL) 94 return; 95 cout << root->val << " "; 96 preOrder(root->left); 97 preOrder(root->right); 98 } 99 100 /*中序遍历*/ 101 void HuffmanTree::inOrder(Node* root) 102 { 103 if (root == NULL) 104 return; 105 inOrder(root->left); 106 cout << root->val << " "; 107 inOrder(root->right); 108 } 109 110 /*后序遍历*/ 111 void HuffmanTree::postOrder(Node* root) 112 { 113 if (root == NULL) 114 return; 115 postOrder(root->left); 116 postOrder(root->right); 117 cout << root->val << " "; 118 } 119 120 /*销毁哈夫曼树*/ 121 void HuffmanTree::destroyTree(Node* root) 122 { 123 if (root == NULL) 124 return; 125 destroyTree(root->left); 126 destroyTree(root->right); 127 delete root; 128 } 129 130 int main() 131 { 132 /*创建哈夫曼树*/ 133 HuffmanTree* huffmanTree = new HuffmanTree(); 134 Node* root = huffmanTree->create(); 135 136 cout << "先序遍历:"; 137 huffmanTree->preOrder(root); 138 cout << endl; 139 140 cout << "中序遍历:"; 141 huffmanTree->inOrder(root); 142 cout << endl; 143 144 cout << "后序遍历:"; 145 huffmanTree->postOrder(root); 146 cout << endl; 147 148 return 0; 149 }
结果:
先序遍历:15 6 3 3 1 2 9 4 5 中序遍历:3 6 1 3 2 15 4 9 5 后序遍历:3 1 2 3 6 4 5 9 15
三、哈夫曼编码
我们约定左分支表示字符'0',右分支表示字符'1',在哈夫曼树中从根结点开始,到叶子结点的路径上分支字符组成的字符串为该叶子结点的哈夫曼编码。上面代码所创建的哈夫曼树如下所示:

可以看出3被编码为00,1为010,2为011,4为10,5为11。在这些编码中,任何一个字符的编码均不是另一个字符编码的前缀。
实现代码:
/*哈夫曼编码*/ void HuffmanTree::encode(Node* root, string code) { if (root->left == NULL&&root->right == NULL) //叶子结点 cout << root->val << " 被编码为 " << code << endl; if (root->left != NULL) { code += "0"; //左子树,编码code添加'0' encode(root->left, code); code.erase(code.end()-1); //删除上一步添加的'0' } if (root->right != NULL) { code += "1"; //右子树,编码code添加'1' encode(root->right, code); code.erase(code.end()-1); //删除上一步添加的'1' } }
完整代码:
#include <iostream> #include <queue> #include <string> #include <iomanip> using namespace std; class Node { public: int val; //结点的值 Node* left; //结点左孩子 Node* right; //结点右孩子 Node* parent; //结点的父结点 Node(int val) :val(val), left(NULL), right(NULL), parent(NULL) {} Node(int val, Node* left, Node* right, Node* parent) :val(val), left(left), right(right), parent(parent) {} }; class Compare //比较类,用于构造Node*类型的priority_queue { public: bool operator() (Node* a, Node* b) { return a->val > b->val; //结点的值越小越靠前 } }; class HuffmanTree { private: priority_queue<Node*, vector<Node*>, Compare> nodes; //优先队列(小根堆) Node* root; public: HuffmanTree(); ~HuffmanTree(); /*创建哈夫曼树,返回根结点*/ Node* create(); /*哈夫曼编码*/ void encode(Node* node, string code); /*先序遍历*/ void preOrder(Node* root); /*中序遍历*/ void inOrder(Node* root); /*后序遍历*/ void postOrder(Node* root); /*销毁哈夫曼树*/ void destroyTree(Node* root); }; HuffmanTree::HuffmanTree() { while (!nodes.empty()) nodes.pop(); int a[] = { 4,3,5,1,2 }; int len = sizeof(a) / sizeof(a[0]); for (int i = 0;i < len; i++) //使用数组的值初始化结点 nodes.push(new Node(a[i])); root = NULL; } HuffmanTree::~HuffmanTree() { destroyTree(root); } Node* HuffmanTree::create() { while (nodes.size() > 1) { Node* node1 = nodes.top(); //选取结点值最小的两个结点 nodes.pop(); Node* node2 = nodes.top(); nodes.pop(); Node* root = new Node(node1->val + node2->val); //新结点的值为两个结点值之和 root->left = node1; //将新结点设为两结点的根结点 root->right = node2; node1->parent = root; node2->parent = root; nodes.push(root); } root = nodes.top(); //队列中最后一个结点即为哈夫曼树的根结点 nodes.pop(); return root; } /*哈夫曼编码*/ void HuffmanTree::encode(Node* root, string code) { if (root->left == NULL&&root->right == NULL) //叶子结点 cout << root->val << " 被编码为 " << code << endl; if (root->left != NULL) { code += "0"; //左子树,编码code添加'0' encode(root->left, code); code.erase(code.end()-1); //删除上一步添加的'0' } if (root->right != NULL) { code += "1"; //右子树,编码code添加'1' encode(root->right, code); code.erase(code.end()-1); //删除上一步添加的'1' } } /*先序遍历*/ void HuffmanTree::preOrder(Node* root) { if (root == NULL) return; cout << root->val << " "; preOrder(root->left); preOrder(root->right); } /*中序遍历*/ void HuffmanTree::inOrder(Node* root) { if (root == NULL) return; inOrder(root->left); cout << root->val << " "; inOrder(root->right); } /*后序遍历*/ void HuffmanTree::postOrder(Node* root) { if (root == NULL) return; postOrder(root->left); postOrder(root->right); cout << root->val << " "; } /*销毁哈夫曼树*/ void HuffmanTree::destroyTree(Node* root) { if (root == NULL) return; destroyTree(root->left); destroyTree(root->right); delete root; } int main() { /*创建哈夫曼树*/ HuffmanTree* huffmanTree = new HuffmanTree(); Node* root = huffmanTree->create(); cout << "先序遍历:"; huffmanTree->preOrder(root); cout << endl; cout << "中序遍历:"; huffmanTree->inOrder(root); cout << endl; cout << "后序遍历:"; huffmanTree->postOrder(root); cout << endl; cout << "哈夫曼编码:" << endl; huffmanTree->encode(root, ""); return 0; }
结果:
先序遍历:15 6 3 3 1 2 9 4 5 中序遍历:3 6 1 3 2 15 4 9 5 后序遍历:3 1 2 3 6 4 5 9 15 哈夫曼编码: 3 被编码为 00 1 被编码为 010 2 被编码为 011 4 被编码为 10 5 被编码为 11


 浙公网安备 33010602011771号
浙公网安备 33010602011771号