知识学报：入门（1）

不是题解不是教学！！！

11.19

CSES 1068

模拟。

CSES 1083

模拟。

CSES 1069

模拟。

CSES 1094

每次操作对某个数加一，要求从左到右不减小，求最小操作次数。
从左到右每个检查，如不满足就加到和前一个相同。

CSES 1070

要求给出一个长度为 \(n\) 的排列使没有相邻的数相邻，或输出无解。
显然 \(1\) 是一个相邻数最少的数所以放在中间，然后随便填，\(2\) 放在最边上是一种构造方案，可以得到 \(4\) 或以上才有解。考虑比较容易写的方法，可以偶数从小到大放，再奇数从小到大放。注意 \(n=1\) 时也有解。

CSES 1071

对一个形如：

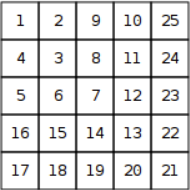
的矩阵，给出 \(x\) 和 \(y\) 求数字。
发现每层结尾都是一个完全平方数，且为坐标中最大值的平方。于是计算出结尾再根据奇偶性计算这个数即可。

CSES 1072

对于一个 \(k \times k\) 的棋盘有多少种放两个互不攻击的骑士的方案。
容斥原理，总方案数减能攻击方案数就是互不攻击的方案。总方案数为 \(\frac{k^2 \times (k^2 - 1)}{2}\)，互相攻击的情况是一个 \(2 \times 3\) 或 \(3 \times 2\) 的格子，攻击方案数为 \(4(k-1)(k-2)\)，相减即为答案。

CSES 1092

给定一个长度为 \(n\) 的排列，求分成两组使两组和相同的分配方案，或输出无解。
当排列和为奇数时无解，偶数时有解。从大到小塞入第一组，如果塞入后不超过总和的一半则塞入，否则不塞。剩下的就是第二组。

CSES 1617

求长度为 \(n\) 的二进制串有多少种。
输出 \(2^n\) 即可。

CSES 1618

求 \(n!\) 的结尾有几个零。
有几个零即为求该数的因子 \(10\) 的个数，即求 \(2\) 和 \(5\) 因子中较小的那个。求解 \(n!\) 中某个质因子个数，可以用定理，即 \(p\) 因子个数为 \(\lfloor\frac{n}{p}\rfloor + \lfloor\frac{n}{p^2}\rfloor + \lfloor\frac{n}{p^3}\rfloor +...\)，意义为恰为 \(p\) 倍数的贡献 \(1\) 个因子，为 \(p^2\) 的额外贡献一个因子 \(p\)，\(p^3\) 再额外贡献一个，以此类推。