PyTorch中的乘法

PyTorch中的乘法包括 '*'、 'torch.mul'、 'torch.dot', 'torch.matmul'、 'torch.mm'、 'torch.bmm', '@'、 'torch.tensordot'、 'torch.einsum'.

1. * 和 torch.mul

'*' 和 torch.mul 都表示对应元素相乘

a = torch.tensor([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
b = torch.tensor([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
c = torch.tensor([[2]])
d = torch.tensor([[1, 2, 3]])
e = torch.tensor([[1], [2], [3]])
f = torch.tensor([[1, 2, 3], [4, 5, 6]])
# ------------------------------------------------------
print(f"a * b: \n{a * b},\ntorch.mul(a, b): \n{torch.mul(a, b)}")
print(f"a * c: \n{a * c},\ntorch.mul(a, c): \n{torch.mul(a, c)}")
print(f"a * d: \n{a * d},\ntorch.mul(a, d): \n{torch.mul(a, d)}")
print(f"a * e: \n{a * e},\ntorch.mul(a, e): \n{torch.mul(a, e)}")
print(f"a * f: \n{a * f},\ntorch.mul(a, f): \n{torch.mul(a, f)}")

结果如下:

a * b: 
tensor([[ 1,  4,  9],
        [16, 25, 36],
        [49, 64, 81]]),
torch.mul(a * b): 
tensor([[ 1,  4,  9],
        [16, 25, 36],
        [49, 64, 81]])
# ------------------------------------
a * c: 
tensor([[ 2,  4,  6],
        [ 8, 10, 12],
        [14, 16, 18]]),
torch.mul(a * c): 
tensor([[ 2,  4,  6],
        [ 8, 10, 12],
        [14, 16, 18]])
# -------------------------------------
a * d: 
tensor([[ 1,  4,  9],
        [ 4, 10, 18],
        [ 7, 16, 27]]),
torch.mul(a * d): 
tensor([[ 1,  4,  9],
        [ 4, 10, 18],
        [ 7, 16, 27]])
# -------------------------------------
a * e: 
tensor([[ 1,  2,  3],
        [ 8, 10, 12],
        [21, 24, 27]]),
torch.mul(a * e): 
tensor([[ 1,  2,  3],
        [ 8, 10, 12],
        [21, 24, 27]])
# -------------------------------------
# RuntimeError: The size of tensor a (3) must match the size of tensor b (2) 
# at non-singleton dimension 0

总结: 虽然说对应元素相乘并不一定要求两个矩阵要完全行数和列数相等, 但也要能有正确的广播机制.

2. torch.dot

只用来计算两个一维tensor的点积, 这一点和numpy中的.dot()不太一样

a = torch.tensor([1, 2])
b = torch.tensor([3, 4])
c = torch.tensor([[1, 2, 3], [4, 5, 6]])  # (2, 3)
d = torch.tensor([[1, 2], [3, 4], [5, 6]])  # (3, 2)
# ----------------------------------------------------
print(f"torch.dot(a, b): \n{torch.dot(a, b)},\nnp.dot(a, b): \n{np.dot(a, b)}")
print(f"np.dot(c, d): \n{np.dot(c, d)}")
print(f"torch.dot(c, d): \n{torch.dot(c, d)}")

结果如下:

torch.dot(a, b): 
11,
np.dot(a, b): 
11
# --------------------------------------
np.dot(c, d): 
[[22 28]
 [49 64]]
# --------------------------------------
# RuntimeError: 1D tensors expected, but got 2D and 2D tensors

3. torch.tensordot()

torch.tensordot()是torch.dot()的升级版, 可以指定两个tensor在哪个维度做内积
话不多说, 举例如下:

a = torch.tensor([[1, 2, 3, 4], [5, 6, 7, 8], [9, 0, 1, 2]])  # (3, 4)
b = torch.tensor([[1, 2], [3, 4], [5, 6], [7, 8]])  # (4, 2)
print(f"torch.tensordot(a, b, dims=([1], [0])): \n{torch.tensordot(a, b, dims=([1], [0]))}")

结果如下:

torch.tensordot(a, b, dims=([1], [0])): 
tensor([[ 50,  60],
        [114, 140],
        [ 28,  40]])

a = torch.randn(3, 4, 3)  # (3, 4, 3), (0, 1, 2)
b = torch.randn(4, 3, 4)  # (4, 2)
print(f"torch.tensordot(a, b, dims=([1], [0])).shape: \n{torch.tensordot(a, b, dims=([1], [0])).shape}")
print(f"torch.tensordot(a, b, dims=([1, 2], [0, 1])).shape: \n{torch.tensordot(a, b, dims=([1, 2], [0, 1])).shape}")
print(f"torch.tensordot(a, b, dims=([0, 1], [1, 2])).shape: \n{torch.tensordot(a, b, dims=([0, 1], [1, 2])).shape}")
print(f"torch.tensordot(a, b, dims=([0], [1])).shape: \n{torch.tensordot(a, b, dims=([0], [1])).shape}")
print(f"torch.tensordot(a, b, dims=([0, 1], [1, 0])).shape: \n{torch.tensordot(a, b, dims=([0, 1], [1, 0])).shape}")
print(f"torch.tensordot(a, b, dims=(`[1, 2], [2, 1]`)).shape: \n{torch.tensordot(a, b, dims=([1, 2], [2, 1])).shape}")

结果如下:

torch.tensordot(a, b, dims=([1], [0])).shape: 
torch.Size([3, 3, 3, 4])
torch.tensordot(a, b, dims=([1, 2], [0, 1])).shape: 
torch.Size([3, 4])
torch.tensordot(a, b, dims=([0, 1], [1, 2])).shape: 
torch.Size([3, 4])
torch.tensordot(a, b, dims=([0], [1])).shape: 
torch.Size([4, 3, 4, 4])
torch.tensordot(a, b, dims=([0, 1], [1, 0])).shape: 
torch.Size([3, 4])
torch.tensordot(a, b, dims=(`[1, 2], [2, 1]`)).shape: 
torch.Size([3, 4])

4. torch.mm

mm: matrix matrix, 只用来计算两个二维矩阵的乘法

a = torch.tensor([[1, 2, 3], [4, 5, 6]])  # (2, 3)
b = torch.tensor([[1, 2], [3, 4], [5, 6]])  # (3, 2)
# ------------------------------------------------------
print(f"torch.mm(a, b): \n{torch.mm(a, b)}")
print(f"torch.mm(a, a): \n{torch.mm(a, a)}")

结果如下:

torch.mm(a, b): 
tensor([[22, 28],
        [49, 64]])
# -----------------
# RuntimeError: mat1 and mat2 shapes cannot be multiplied (2x3 and 2x3)
# -----------------

5. torch.bmm(bmat1, bmat2, out=None)

bmm: batch matrix matrix, 其中bmat1(B, n, m), bmat2(B, m, d)
要求两个矩阵必须是三维矩阵, 而且第一维度相同, 表示批次的意思

a = torch.randn((3, 2, 3))
b = torch.randn((3, 3, 4))
# ------------------------------
print(f"torch.bmm(a, b): \n{torch.bmm(a, b).shape}")  # (3, 2, 4)

结果如下:

torch.Size([3, 2, 4])

6. torch.matmul(input, other, out=None)

两个tensor之间的矩阵乘法, 没有维度的要求, 只要符合计算条件即可

• 如果两个矩阵都是一维的，那么该函数的功能与torch.dot()一样，返回两个一维tensor的点乘结果

a = torch.tensor([1, 2, 3])
print(f"torch.dot(a, a): \n{torch.dot(a, a)}")
print(f"torch.matmul(a, a): \n{torch.matmul(a, a)}")

结果如下:

torch.dot(a, a): 
14
torch.matmul(a, a): 
14

• 当input和other均是二维张量时, torch.matmul()与torch.mm()结果相同

a = torch.tensor([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
print(f"torch.mm(a, a): \n{torch.mm(a, a)}")
print(f"torch.matmul(a, a): \n{torch.matmul(a, a)}")

结果如下

torch.mm(a, a): 
tensor([[ 30,  36,  42],
        [ 66,  81,  96],
        [102, 126, 150]])
torch.matmul(a, a): 
tensor([[ 30,  36,  42],
        [ 66,  81,  96],
        [102, 126, 150]])

• 如果第一个tensor是一维的而第二个tensor是二维的，那么会在第一个tensor的维度上增加一个维度，然后执行二维矩阵乘法，最后将预填充的维度1去掉
• 如果第一个tensor是二维或者二维以上的，而第二个tensor是一维的，那么将执行矩阵-向量乘法

a = torch.tensor([1, 2, 3])
b = torch.tensor([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
print(f"torch.matmul(a, b): \n{torch.matmul(a, b)}")
print(f"torch.matmul(b, a): \n{torch.matmul(b, a)}")

结果如下

torch.matmul(a, b): 
tensor([30, 36, 42])
torch.matmul(b, a): 
tensor([14, 32, 50])

• 如果两个tensor都至少是一维的，而且至少一个tensor的维度大于2，那么会发生批处理矩阵乘法

a = torch.tensor([1, 2, 3])
b = torch.tensor([
    [[1, 2], [4, 5], [7, 8]],
    [[7, 8], [4, 5], [1, 2]],
    [[4, 5], [7, 8], [1, 2]],
    [[1, 2], [7, 8], [4, 5]]
])
c = torch.tensor([1, 2])
print(f"torch.matmul(a, b): \n{torch.matmul(a, b)}")
print(f"torch.matmul(b, c): \n{torch.matmul(b, c)}")

结果如下:

torch.matmul(a, b): 
tensor([[30, 36],
        [18, 24],
        [21, 27],
        [27, 33]])
torch.matmul(b, c): 
tensor([[ 5, 14, 23],
        [23, 14,  5],
        [14, 23,  5],
        [ 5, 23, 14]])

• 如果第二个是二维的呢？

b = torch.tensor([
    [[1, 2, 3], [4, 5, 6], [7, 8, 9]],
    [[7, 8, 9], [4, 5, 6], [1, 2, 3]],
    [[4, 5, 6], [7, 8, 9], [1, 2, 3]],
    [[1, 2, 3], [7, 8, 9], [4, 5, 6]]
])
c = torch.tensor([[1, 2], [3, 4], [5, 6]])
print(f"torch.matmul(b, c): \n{torch.matmul(b, c)}")  # torch.Size([4, 3, 2])

结果如下:

torch.matmul(b, c): 
tensor([[[ 22,  28],
         [ 49,  64],
         [ 76, 100]],

        [[ 76, 100],
         [ 49,  64],
         [ 22,  28]],

        [[ 49,  64],
         [ 76, 100],
         [ 22,  28]],

        [[ 22,  28],
         [ 76, 100],
         [ 49,  64]]])

7. torch.einsum()

这个方法就厉害了，号称满足所有关于张量之间的计算（点积、外积、转置、乘法）需求，可以参考这位大佬写的https://zhuanlan.zhihu.com/p/44954540
关于eiusum的调用格式如下:

话不多说，直接上例子吧

• 矩阵转置

a = torch.tensor([[1, 2, 3], [4, 5, 6]])
print(f"torch.einsum('ij -> ji', a): \n{torch.einsum('ij -> ji', a)}")

结果如下:

torch.einsum('ij -> ji', a): 
tensor([[1, 4],
        [2, 5],
        [3, 6]])

• 求和

a = torch.tensor([[1, 2, 3], [4, 5, 6]])
print(f"torch.einsum('ij ->', a): \n{torch.einsum('ij ->', a)}")

结果如下:

torch.einsum('ij ->', a): 
21

• 行、列求和

a = torch.tensor([[1, 2, 3], [4, 5, 6]])
print(f"torch.einsum('ij -> i', a): \n{torch.einsum('ij -> i', a)}")
print(f"torch.einsum('ij -> j', a): \n{torch.einsum('ij -> j', a)}")

结果如下:

torch.einsum('ij -> i', a): 
tensor([ 6, 15])
torch.einsum('ij -> j', a): 
tensor([5, 7, 9])

• 矩阵-向量相乘
  

a = torch.arange(6).reshape(2, 3)
b = torch.arange(3)
print(f"torch.einsum('ik,k->i', [a, b]): \n{torch.einsum('ik,k->i', [a, b])}")

结果如下:

torch.einsum('ik,k->i', [a, b]): 
tensor([ 5, 14])

• 矩阵-矩阵相乘
  

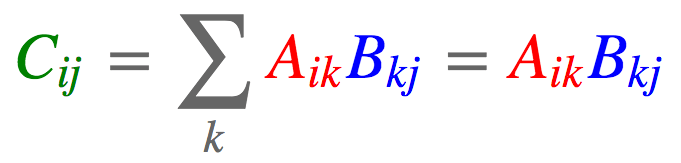
a = torch.arange(6).reshape(2, 3)
b = torch.arange(15).reshape(3, 5)
print(f"torch.einsum('ik,kj->ij', [a, b]): \n{torch.einsum('ik,kj->ij', [a, b])}")

结果如下:

torch.einsum('ik,kj->ij', [a, b]): 
tensor([[ 25,  28,  31,  34,  37],
        [ 70,  82,  94, 106, 118]])

• 向量、矩阵点积
  
  

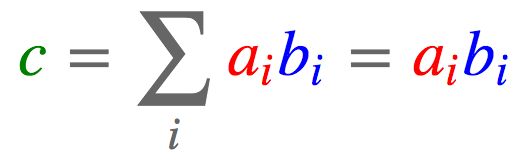
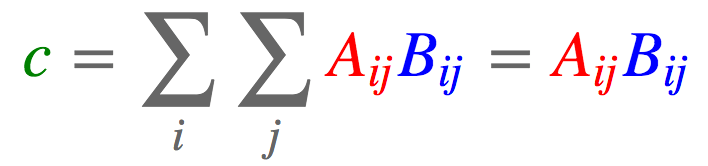
a = torch.arange(3)
b = torch.arange(3,6)  # [3, 4, 5]
c = torch.arange(6).reshape(2, 3)
d = torch.arange(6,12).reshape(2, 3)
print(f"torch.einsum('i,i->', [a, b]): \n{torch.einsum('i,i->', [a, b])}")
print(f"torch.einsum('ij,ij->', [c, d]): \n{torch.einsum('ij,ij->', [c, d])}")

结果如下:

torch.einsum('i,i->', [a, b]): 
14
torch.einsum('ij,ij->', [c, d]): 
145

• 哈达玛积

a = torch.arange(6).reshape(2, 3)
b = torch.arange(6,12).reshape(2, 3)
print(f"torch.einsum('ij,ij->ij', [a, b]): \n{torch.einsum('ij,ij->ij', [a, b])}")

结果如下:

torch.einsum('ij,ij->ij', [a, b]): 
tensor([[ 0,  7, 16],
        [27, 40, 55]])

• 外积

a = torch.arange(3)
b = torch.arange(3,7)
print(f"torch.einsum('i,j->ij', [a, b]): \n{torch.einsum('i,j->ij', [a, b])}")

结果如下：

torch.einsum('i,j->ij', [a, b]): 
tensor([[ 0,  0,  0,  0],
        [ 3,  4,  5,  6],
        [ 6,  8, 10, 12]])

• batch矩阵相乘
  

a = torch.randn(3,2,5)
b = torch.randn(3,5,3)
print(f"torch.einsum('ijk,ikl->ijl', [a, b]): \n{torch.einsum('ijk,ikl->ijl', [a, b])}")

结果如下:

torch.einsum('ijk,ikl->ijl', [a, b]): 
tensor([[[ 1.1878,  0.3985, -2.4245],
         [ 2.6813,  0.7718, -1.1574]],

        [[ 5.0665,  0.0867,  1.4942],
         [-1.0865, -1.0211, -0.8185]],

        [[ 3.3403,  3.9011,  3.4569],
         [ 2.1538,  0.8724,  0.6018]]])

• 张量缩约
  

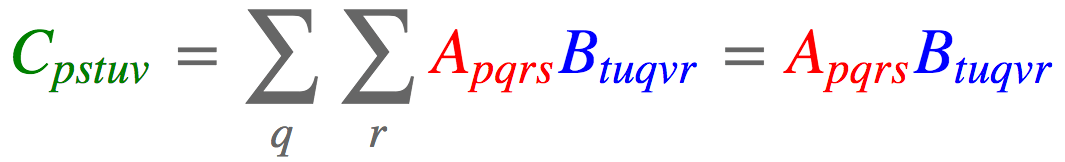
a = torch.randn(2,3,5,7)
b = torch.randn(11,13,3,17,5)
print(f"torch.einsum('pqrs,tuqvr->pstuv', [a, b]).shape: \n{torch.einsum('pqrs,tuqvr->pstuv', [a, b]).shape}")

结果如下:

torch.einsum('pqrs,tuqvr->pstuv', [a, b]).shape: 
torch.Size([2, 7, 11, 13, 17])