最大权闭合子图

闭合子图

一个点集，不存在连接点集和点集外的边

最大权闭合子图

点权和最大的闭合子图

把闭合子图的集合映射到流网络的割的集合

原图 \(G(V,E)\)

建一个源点 \(s\) 到所有正权点，容量是点券，建一个汇点 \(t\) 到所有负权点，容量是点权绝对值。原图的所有边不变，容量 \(+\infty\)

原图 \(G\)

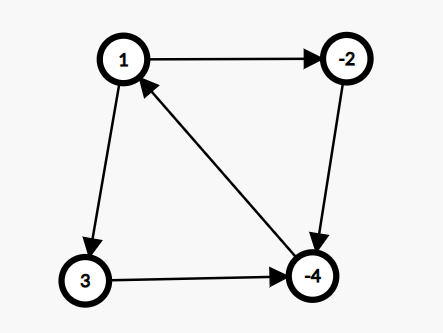
新图 \(G'\)

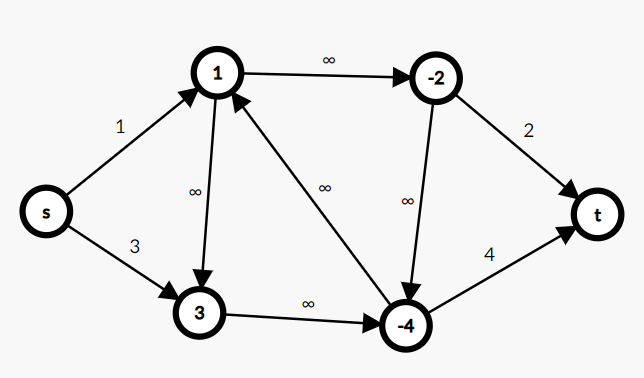
简单割

所有的割边都连接 \(s\) 或 \(t\)

现证明 简单割与闭合子图一一对应

对与闭合子图 \(V\) , $ V$ 中的点只能连接 \(s\) 或 \(t\) ,所以是简单割

对于一个简单割\([S,T]\) ，\(S-\{s\}\) 是一个闭合图，因为连接 \(S\) ，\(T\) 的边必定与 \(s\) 或 \(t\) 相连，所有 \(S-{s}\) 中的边只能连接自己

现在考虑数值上的关系

对于闭合子图 \(V\) , \(V^+\) 表示 \(V\) 中所有正权点的点权之和， \(V^-\) 表示所有负权的的点权绝对值之和

则 \(V\) 的权和为

\[s = V^+ - V^- \]

现在考虑割 \([S,T]\) 的流量， \(S \to T\) 的只有两种边，一种是 \(V\) 到 \(t\) 的边，一种是 \(s\) 到 原图中除去 \(V\) 的其他点, 由于 \(s\) 连接的是正权的点，设原图所有正权点的点权之和是 \(sum\) ，则这部分正权点的点权之和是 \(sum - V^+\)

\[c = V^- + sum - V^+ = sum - s \]

所以至此，要求最大权闭合子图，也就是求图 \(G'\) 的最小割