生成函数(母函数)
生成函数
在数学中,某个序列\((a_n)_{n∈N}\) 的母函数(又称生成函数,英语:\(Generating\ function\))是一种形式幂级数,其每一项的系数可以提供关于这个序列的信息。
普通生成函数
有三种物品,分别有 3 ,2, 3个,问拿四个的方案数
f[i][j] 表示当前第 i 个位置,已经选了 j 个物品的方案数
f[0][0] = 1;
for(int i = 1;i <= 3;i++){
for(int j = 0;j <= 8;j++){//总共要选j个
for(int k = 0;k <= j;k++){//已经选了k个
if(j - k <= v[i])//此时要选j-k个
f[i][j] += f[i-1][k];
}
}
}
第一种物品的生成函数 \(G_1(x) = 1 + x + x^2 + x ^ 3\)
\(G_2(x) = 1 + x + x^2\) , $G_3 = 1 + x + x^2 + x^3 $
\(G_1(x)*G_2(x)*G_3(x)\) ,中 \(x^4\) 的系数就是答案
上述代码其实就是在求多项式乘法的系数
指数生成函数
将上述问题改成排列方案hdu1521

构造出
\(G_1(x) = 1+\frac{x^1}{1} + \frac{x^2}{2!} + \frac{x^3}{3!}\)
\(G_2(x) = 1 + \frac{x^1}{1} + \frac{x^2}{2}\)
\(G_3(x) = 1 + \frac{x^1}{1} + \frac{x^2}{2!} + \frac{x^3}{3!}\)
\[\begin{aligned}G_e(x) &= (1 + \frac{x}{1!} + \frac{x^2}{2!} + \frac{x^3}{3!})(1+\frac{x}{1!} + \frac{x^2}{2!}) (1 + \frac{x}{1!} + \frac{x^2}{2!} + \frac{x^3}{3!})\\ &= (1+2x+2x^2+\frac{7}{6}x^3 + \frac{5}{12}x^4 + \frac{1}{12}x^5) (1+x+\frac{1}{2}x^2 + \frac{1}{6}x^3)\\ &=(1+3x + \frac{9}{2}x^2 + \frac{14}{3}x^3 + \frac{35}{12}x^4 + \frac{17}{12}x^5 + \frac{35}{72} x^6 + \frac{8}{72}x^7 + \frac{1}{71}x^8)\end{aligned}
\]
答案就是 \(x^4\) 的系数乘上 \(4!\) , \(\frac{35}{12} * 4! = 70\)
(1-x)^-1 型
\[\dfrac 1 {1-x} = \sum_{i=0}^\infty x^i
\]

广义二项式定理
\[\dfrac 1 {(1-x)^n} = \sum_{i=0}^{\infty} C_{n+i-1}^i x^i
\]
至多为 \(k\) 就是 \(\dfrac {1-x^{k+1}} {1-x}\)
\(k\) 的倍数就是 \(\dfrac 1 {1-x^k}\)
最后的结果是 \(\dfrac 1 {(1-x)^5}\) , 带入广义二项式定理, 答案是 \(C_n^4\)
\(py\) 草不过去, \(OI\)👴直呼 人生苦短我用 \(ruby\)
e^x 型
\[e^x = \sum_{i=0}^\infty \dfrac {x^i} {i!}
\]
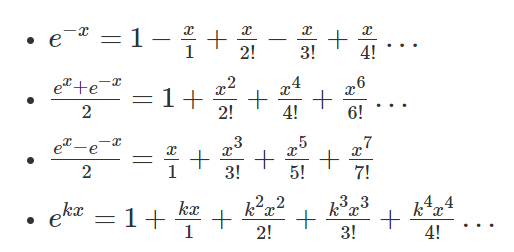


 浙公网安备 33010602011771号
浙公网安备 33010602011771号