二分思想的应用与哈希表使用

抽象题意：求解原字符串中不重复出现的最短子串的长度

s.substr(pos,n) 表示返回一个string，包含原字符串s中从pos开始的共n个字符的拷贝（pos的默认值为0，n的默认值是s.size()-pos，即若不加n这个参数的话，会默认从pos到结尾全部拷贝）

注意：如果pos+n超过了原字符串的大小，则会做出自动修正，将substr需要拷贝的值n改为到string的末尾。

法一：直接暴力求\(O(n^2)\) 没问题

#include <bits/stdc++.h>
using namespace std;
const int N = 110;
int n;
string s;
int main()
{
    cin>>n>>s;
    
    for (int i=1;i<=n;i++)  // 子串长度为1~n
    {
        unordered_set<string>st;  // 集合记录每个长度为i的子串是否出现过
        bool flag = false;
        for (int j=0;j+i<=n;j++) // 每次从j开始遍历枚举
        {
            string t = s.substr(j,i); // 截取到以j为起始位置，长度为i的子串
            if (st.count(t))  // 如果对于当前的子串，已经在之前出现过了，那么i=i+1
            {
                flag = true;
                break;
            }
            else 
                st.insert(t);
        }
        
        if (!flag) // 找到了符合条件的子串
        {
            cout<<i<<endl;
            return 0;
        }
        
    }
    return 0;
}

---

法二：二分

枚举答案\(logn\) ，每次需要\(O(n^2)\)的时间完成子串的记录和查找,\(O(n^2logn)\) 没问题

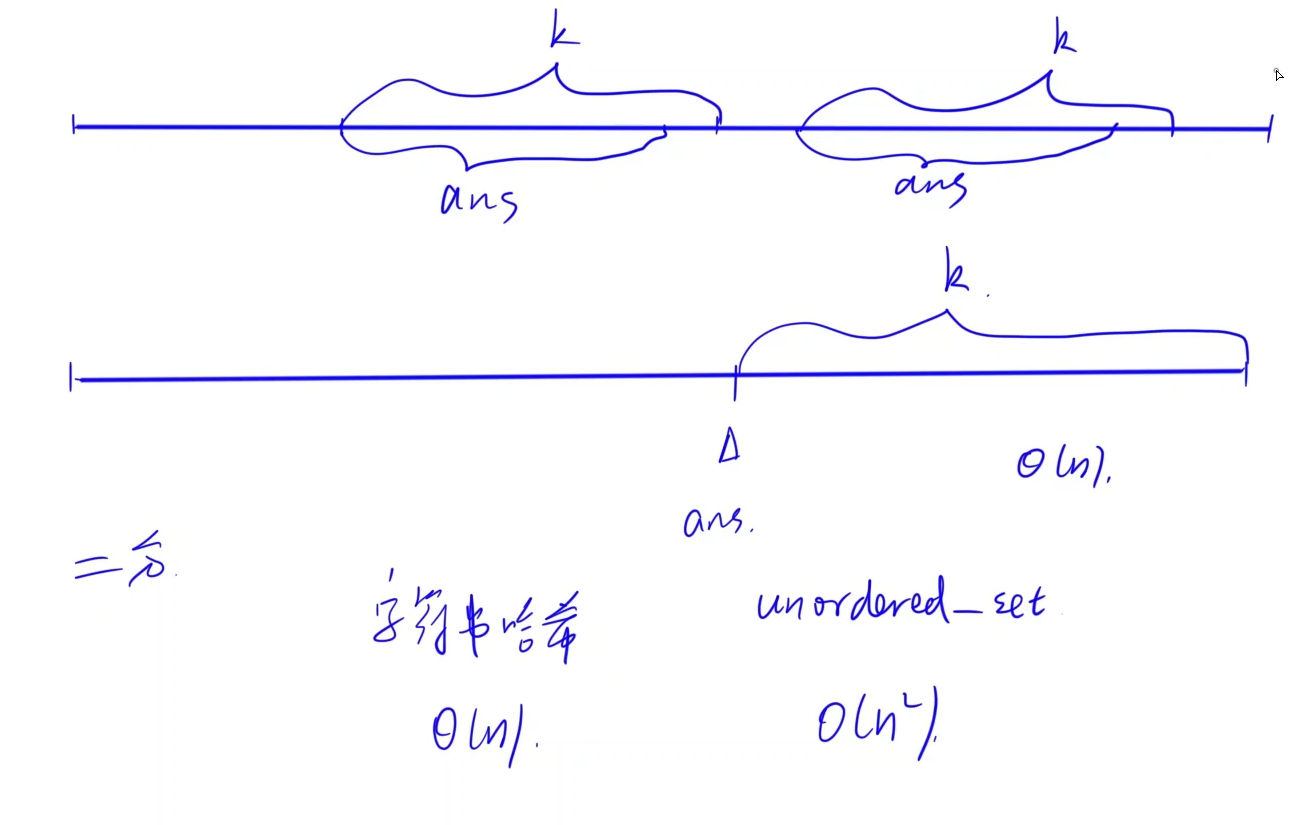
这里的二分思想可以说用的非常的舒适，即目标是找到原字符串中没有重复出现过的子串。

那么假设最终的答案子串ans的长度为k，则说明若子串的长度>k，那么一定会包含答案子串ans；若答案小于k，则一定会在原字符串中重复出现过，因为不重复出现子串的最短长度为k，不可能更短。

---

#include <bits/stdc++.h>
using namespace std;
const int N = 110;
int n;
string s;
bool check(int mid)
{
    unordered_set<string> hash; // 每次check都要开一个哈希表，判断并记录当前字符在之前出现的次数
    for (int i=0;i+mid-1<n;i++)
    {
        string t = s.substr(i,mid); 
        if (hash.count(t))
            return false;
        hash.insert(t);
    }
    
    return true;
}
int main()
{
    cin>>n>>s;
    
    int l =1,r=n; // 答案的范围，即长度为1~n
    while (l<r)
    {
        int mid = l+r>>1;
        if (check(mid)) r=mid; // 说明答案字符串的长度是<=mid的
        else l=mid+1;
    }
    
    cout<<r<<endl;
    return 0;
}

---

感觉现在遇到求最小值的问题，就想分析一下有没有二段性，能不能用二分

---

unordered_set、unordered_map、set

unordered_map

unordered_map是C++中的哈希表，可以在任意类型与类型之间做映射。

• 定义：unordered_map<int,int> hash,unordered_map<string,int> hash
• 插入：hash[key]=value
• 查询：hash[key] 返回value
• 判断：hash.count(key) 返回key出现的次数
• 遍历：

for (auto &item : hash)
{
    cout << item.first << ' ' << item.second << endl;
}

---

unordered_set和set对比

可以看到unordered_set在增删查方面的性能都比set好，但是为什么我们不用unordered_set去代替set呢？因为set还有一个特点就是有序！而在底层方面，unordered_set底层是哈希，set是红黑树。
处理无序数据时建议用unordered_set，如果需要有序那就选set

示例：

set

Input : 1, 8, 2, 5, 3, 9
Output : 1, 2, 3, 5, 8, 9

unordered_set

Input : 1, 8, 2, 5, 3, 9
Output : 9 3 1 8 2 5 (顺序依赖于 hash function)