梯度消失与梯度爆炸

1. 来自哪

• 学习参数，使用梯度下降：
  $W_{n+1}=W_{n-1}-\eta \frac{\partial L}{\partial W_{n-1}}$

2. 原因

• 梯度消失与梯度爆炸其实是一种情况，
  
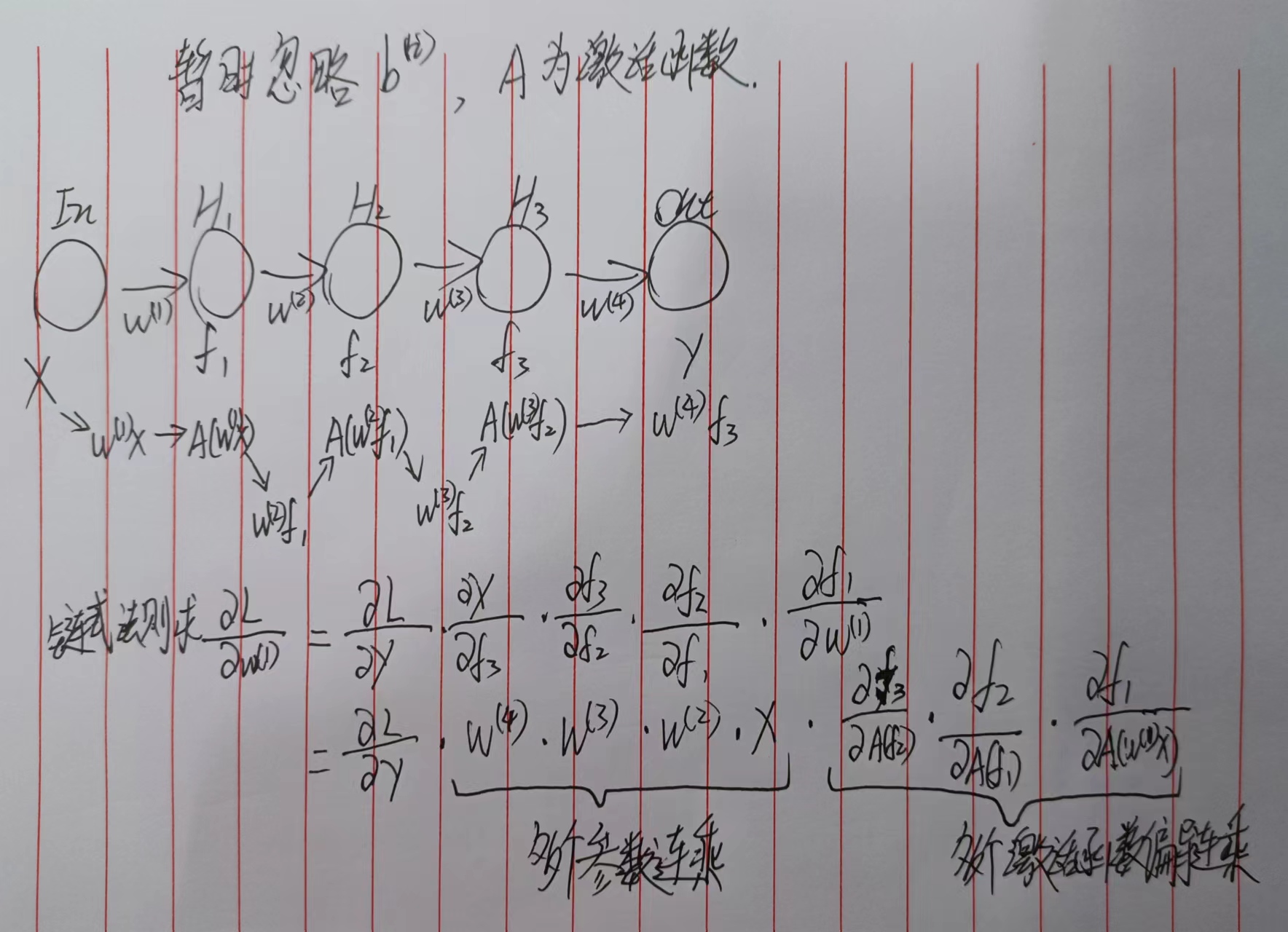
• 由于多层的参数连乘和激活函数的偏导连乘，则两种情况下容易出现梯度问题：
  • 深层网络；
  • 采用的激活函数，比如sigmoid。
• 激活函数求导后与权重相乘的积大于1，那么随着层数增多，求出的梯度更新信息将以指数形式增加，即梯度爆炸；
• 激活函数求导后与权重相乘的积小于1，那么随着层数增多，求出的梯度更新信息将会以指数形式衰减，即梯度消失。

2.1 层数角度

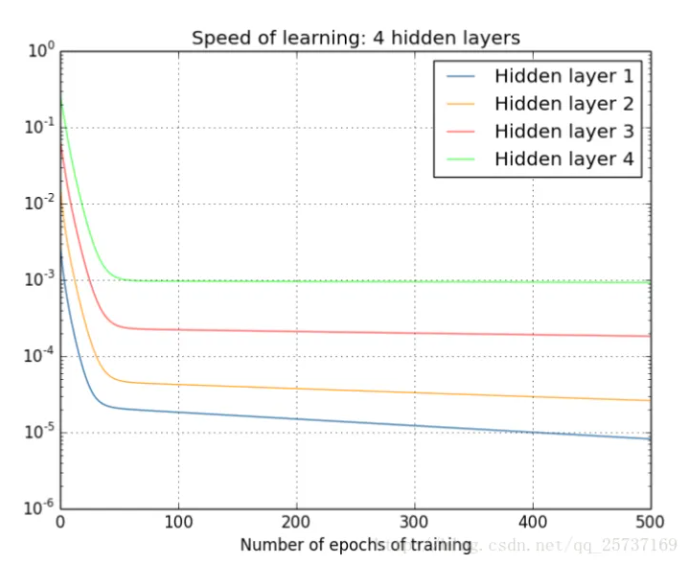
层越多, 式中的两项越多，一旦参数初始化有问题很容易就出现梯度问题。

2.2 激活函数角度

• 两张图够了
  
  
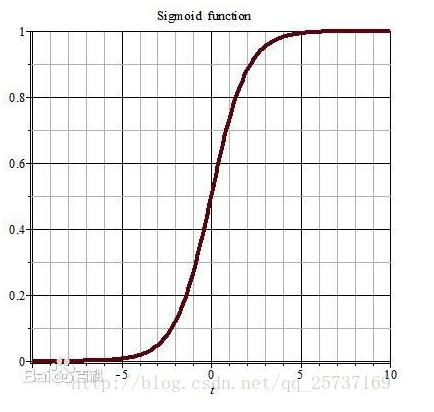
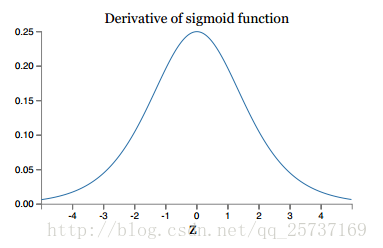
  左侧和右侧的导数趋*于*滑，梯度消失很容易。

3. 如何解决

• 预训练+微调；
• 损失函数内加正则项；
• 激活函数换 relu 等缓解 + 初始化合理一些，例如xiaver初始化。
• BatchNormalization
  通过一定的规范化手段，把每层神经网络任意神经元这个输入值的分布强行拉回到接*均值为0方差为1的标准正太分布，这样使得激活输入值落在非线性函数对输入比较敏感的区域。
• 残差结构

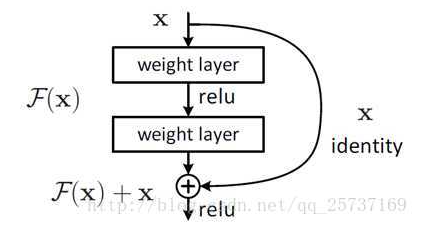
通过前面的信息纠正处理的信息，解决过拟合；
至于梯度爆炸，参考下图