病态矩阵与条件数

本文的阅读等级：高级

当一线性系统受到极微小的扰动即可引发方程解剧烈变化时，我们将无从信任计算结果，便称它是病态系统(见“ 病态系统 ”)。条件数(condition number) 是矩阵运算误差分析的基本工具，它可以度量矩阵对于数值计算的敏感性和稳定性，也可以用来检定病态系统。本文通过一个简单的线性方程扰动问题介绍条件数的推导过程，基本推演工具是矩阵范数 $\Vert A\Vert$ 的定义所含的两个不等式(见“ 矩阵范数 ”)：

$\Vert A+B\Vert\le\Vert A\Vert+\Vert B\Vert$

$\Vert AB\Vert\le\Vert A\Vert\cdot\Vert B\Vert$

问题一 ：考虑线性方程 $A\mathbf{x}=\mathbf{b}$ ，其中 $A$ 为 $n\times n$ 阶可逆矩阵。假设 $\mathbf{b}$ 受到微小扰动成为 $\mathbf{b}+\delta\mathbf{b}$ ，方程解随之由 $\mathbf{x}$ 变为 $\mathbf{x}+\delta\mathbf{x}$ ，试计算相对误差 $\frac{\Vert\delta\mathbf{x}\Vert}{\Vert\mathbf{x}\Vert}$ 的可能范围。

考虑包含扰动及误差的线性方程：

$A(\mathbf{x}+\delta\mathbf{x})=\mathbf{b}+\delta\mathbf{b}$

与原方程式 $A\mathbf{x}=\mathbf{b}$ 相减可得 $A(\delta\mathbf{x})=\delta\mathbf{b}$ ，方程解的误差为 $\delta\mathbf{x}=A^{-1}(\delta\mathbf{b})$ 。利用不等式 $\Vert\delta\mathbf{x}\Vert=\Vert A^{-1}(\delta\mathbf{b})\Vert\le\Vert A^{-1}\Vert\cdot\Vert\delta\mathbf{b}\Vert$ 和 $\Vert\mathbf{b}\Vert=\Vert A\mathbf{x}\Vert\le\Vert A\Vert\cdot\Vert\mathbf{x}\Vert$ ，可得

$\displaystyle\frac{\Vert\delta\mathbf{x}\Vert}{\Vert\mathbf{x}\Vert}=\frac{\Vert A^{-1}(\delta\mathbf{b})\Vert}{\Vert\mathbf{x}\Vert}\le\frac{\Vert A^{-1}\Vert\cdot\Vert\delta\mathbf{b}\Vert}{\Vert\mathbf{x}\Vert}\le\left(\Vert A\Vert\cdot\Vert A^{-1}\Vert\right)\frac{ \Vert\delta\mathbf{b}\Vert}{\Vert\mathbf{b}\Vert}$

另一方面，我们考虑不等式 $\Vert\delta\mathbf{b}\Vert=\Vert A(\delta\mathbf{x})\Vert\le\Vert A\Vert\cdot\Vert\delta\mathbf{x}\Vert$ 和 $\Vert\mathbf{x}\Vert=\Vert A^{-1}\mathbf{b}\Vert\le\Vert A^{-1}\Vert\cdot\Vert\mathbf{b}\Vert$ ，就有

$\displaystyle \frac{\Vert\delta\mathbf{x}\Vert}{\Vert\mathbf{x}\Vert}\ge\frac{\Vert\delta\mathbf{b}\Vert}{\Vert A\Vert\cdot\Vert\mathbf{x}\Vert}\ge\left(\Vert A\Vert\cdot\Vert A^{-1}\Vert\right)^{-1}\frac{\Vert\delta\mathbf{b}\Vert}{\Vert\mathbf{b}\Vert}$

上面二式指出相对误差 $\frac{\Vert\delta\mathbf{x}\Vert}{\Vert\mathbf{x}\Vert}$ 的上下界由矩阵范数乘积 $\Vert A\Vert \cdot\Vert A^{-1}\Vert$ 决定，根据这个结果我们定义方阵 $A$ 的条件数为

$\kappa(A)=\Vert A\Vert\cdot\Vert A^{-1}\Vert$

也就是说， $\delta\mathbf{b}$ 引起的相对误差大小由内部因素 $\kappa(A)$ 和外部因素 $\frac{\Vert\delta\mathbf{b}\Vert}{\Vert\mathbf{b}\Vert}$ 共同决定：

$\displaystyle \kappa(A)^{-1}\frac{\Vert\delta\mathbf{b}\Vert}{\Vert\mathbf{b}\Vert}\le\frac{\Vert\delta\mathbf{x}\Vert}{\Vert\mathbf{x}\Vert}\le\kappa(A)\frac{\Vert\delta\mathbf{b}\Vert}{\Vert\mathbf{b}\Vert}$

接着讨论条件数的计算方法。设 $n\times n$ 阶矩阵 $A$ 的奇异值分解为 $A=U\Sigma V^T$ ，其中 $\Sigma=\mathrm{diag}(\sigma_1,\ldots,\sigma_n)$ ， $\sigma_1\ge\cdots\ge\sigma_n\ge 0$ ， $U$ 和 $V$ 为正交矩阵(见“ 奇异值分解(SVD) ”)。若 $A$ 为可逆矩阵， $\mathrm{rank}A=n$ ，所以 $\sigma_i>0$ ， $i=1,\ldots,n$ 。因为正交矩阵 $U$ 和 $V$ 不改变向量长度，最大奇异值和最小奇异值分别满足

$\displaystyle \sigma_1=\max_{\Vert\mathbf{x}\Vert=1}\Vert\Sigma\mathbf{x}\Vert=\max_{\Vert\mathbf{x}\Vert=1}\Vert A\mathbf{x}\Vert=\Vert A\Vert_2$

$\displaystyle \sigma_n=\min_{\Vert\mathbf{x}\Vert=1}\Vert\Sigma\mathbf{x}\Vert=\min_{\Vert\mathbf{x}\Vert=1}\Vert A\mathbf{x}\Vert=\frac{1}{\Vert A^{-1}\Vert_2}$

以2-范数(2-norm) 计算的条件数也就为

$\displaystyle \kappa(A)=\Vert A\Vert_2\cdot\Vert A^{-1}\Vert_2=\frac{\sigma_1}{\sigma_n}\ge 1$

若 $A$ 为对称可逆矩阵，计算

$A^2=AA^T=(U\Sigma V^T)(V\Sigma U^T)=U\Sigma^2U^T$

因此 $\sigma_i=\vert\lambda_i\vert$ ， $i=1,\ldots,n$ ， $\lambda_i$ 是 $A$ 的特征值，条件数可表示为

$\displaystyle \kappa(A)=\left|\frac{\lambda_1}{\lambda_n}\right|$

又若 $A$ 为正交矩阵， $A^T=A^{-1}$ ，则 $\sigma_1=\cdots=\sigma_n=1$ ，故 $\kappa(A)=1$ ，这说明正交矩阵具有最佳的数值稳定性。

下面我们进一步讨论奇异值分解与条件数上下界的关系。奇异值分解的 $U$ 矩阵其行向量 $\mathbf{u}_1,\ldots,\mathbf{u}_n$ 称为左奇异向量， $V$ 矩阵的行向量 $\mathbf{v}_1,\ldots,\mathbf{v}_n$ 称为右奇异向量，左右奇异向量的关系如下：

$A\mathbf{v}_j=\sigma_j\mathbf{u}_j,~~~j=1,\ldots,n$

考虑 $\mathbf{b}=\alpha\mathbf{u}_1$ ， $\delta\mathbf{b}=\beta\mathbf{u}_n$ ，方程解和误差可分别表示为

$\displaystyle \mathbf{x}=A^{-1}\mathbf{b}=A^{-1}(\alpha\mathbf{u}_1)=\frac{\alpha}{\sigma_1}\mathbf{v}_1$

$\displaystyle \delta\mathbf{x}=A^{-1}(\delta\mathbf{b})=A^{-1}(\beta\mathbf{u}_n)=\frac{\beta}{\sigma_n}\mathbf{v}_n$

计算向量长度并相除，

$\displaystyle\frac{\Vert\delta\mathbf{x}\Vert}{\Vert\mathbf{x}\Vert}=\left(\frac{\sigma_1}{\sigma_n}\right)\frac{\vert\beta\vert}{\vert\alpha\vert}=\kappa(A)\frac{\Vert\delta\mathbf{b}\Vert}{\Vert\mathbf{b}\Vert}$

得知 $\mathbf{b}=\alpha\mathbf{u}_1$ ， $\delta\mathbf{b}=\beta\mathbf{u}_n$ 满足相对误差的上界。同样方式也可以证明 $\mathbf{b}=\alpha\mathbf{u}_n$ ， $\delta\mathbf{b}=\beta\mathbf{u}_1$ 满足相对误差的下界，亦即

$\displaystyle\frac{\Vert\delta\mathbf{x}\Vert}{\Vert\mathbf{x}\Vert}=\left(\frac{\sigma_n}{\sigma_1}\right)\frac{\vert\beta\vert}{\vert\alpha\vert}=\kappa(A)^{-1}\frac{\Vert\delta\mathbf{b}\Vert}{\Vert\mathbf{b}\Vert}$

考虑下面两个取自“ 病态系统 ”一文的例子：

$A=\begin{bmatrix} .540&.387\\ .647&.323 \end{bmatrix},~B=\begin{bmatrix} .540&.323\\ .647&.387 \end{bmatrix}$

计算奇异值后代入条件数公式：

$\begin{aligned} \kappa(A)&=.978920/.077605=12.614\\ \kappa(B)&=.981991/.000001=981,991\approx 10^{6}\end{aligned}$

此例中， $\kappa(A)$ 小(指 $10^{\gamma}$ 的幂 $\gamma$ )， $A$ 是良置的，小扰动 $\delta\mathbf{b}$ 不至于对方程解造成大误差。但 $\kappa(B)$ 很大， $B$ 是病态的，小扰动 $\delta\mathbf{b}$ 可能引起大 $\delta\mathbf{x}$ ，但大扰动 $\delta\mathbf{b}$ 也可能产生微小的 $\delta\mathbf{x}$ 。由于难以掌握 $\delta\mathbf{b}$ 的变化方向，在面对病态系统时我们总是要预防最坏的情形发生。

问题二 ：如果线性方程 $A\mathbf{x}=\mathbf{b}$ 的系数矩阵 $A$ 和常数向量 $\mathbf{b}$ 都受到杂音干扰，这对方程解 $\mathbf{x}$ 的误差有何影响？

考虑 $A$ 和 $\mathbf{b}$ 分别受到 $\delta A$ 和 $\delta\mathbf{b}$ 干扰，则 $\delta\mathbf{x}$ 满足

$(A+\delta A)(\mathbf{x}+\delta\mathbf{x})=\mathbf{b}+\delta\mathbf{b}$

为简化问题，以下假设 $\frac{\Vert\delta A\Vert}{\Vert A\Vert}\le\epsilon$ ， $\frac{\Vert\delta\mathbf{b}\Vert}{\Vert\mathbf{b}\Vert}\le\epsilon$ 。令 $k=\epsilon\kappa(A)$ ，当 $\epsilon<\frac{1}{\kappa(A)}$ 时，下面三个性质成立。

性质一 ： $A+\delta A$ 为可逆矩阵。

已知 $A$ 是可逆的，由假设条件可得

$\Vert A^{-1}(\delta A)\Vert\le\Vert A^{-1}\Vert\cdot\Vert\delta A\Vert\le\epsilon\Vert A^{-1}\Vert\cdot\Vert A\Vert=k<1$

根据Neumann 无穷级数性质可知 $I+A^{-1}(\delta A)$ 是可逆的，且 $\Vert(I+A^{-1}(\delta A))^{-1}\Vert\le\frac{1}{1-k}$ (见“ Neumann无穷级数 ”)，故 $A(I+A^{-1}(\delta A))= A+\delta A$ 亦为可逆矩阵。

性质二 ： $\displaystyle\frac{\Vert\mathbf{x}+\delta\mathbf{x}\Vert}{\Vert\mathbf{x}\Vert}\le\frac{1+k}{1-k}$

将 $(A+\delta A)(\mathbf{x}+\delta\mathbf{x})=\mathbf{b}+\delta\mathbf{b}$ 等号两边左乘 $A^{-1}$ ，

$(I+A^{-1}(\delta A))(\mathbf{x}+\delta\mathbf{x})=\mathbf{x}+A^{-1}(\delta\mathbf{b})$

性质一指出 $I+A^{-1}(\delta A)$ 是可逆的，就有

$\mathbf{x}+\delta\mathbf{x}=( I+A^{-1}(\delta A))^{-1}(\mathbf{x}+A^{-1}(\delta\mathbf{b}))$

利用性质一的不等式，可得

$\displaystyle \Vert\mathbf{x}+\delta\mathbf{x}\Vert\le\Vert(I+A^{-1}(\delta A))^{-1}\Vert\cdot(\Vert\mathbf{x}\Vert+\epsilon\Vert A^{-1}\Vert\cdot\Vert\mathbf{b}\Vert)\le\frac{1}{1-k}\left(\Vert\mathbf{x}\Vert+k\frac{\Vert\mathbf{b}\Vert}{\Vert A\Vert}\right)$

但 $\Vert\mathbf{b}\Vert=\Vert A\mathbf{x}\Vert\le\Vert A\Vert\cdot\Vert\mathbf{x}\Vert$ ，所以

$\displaystyle \Vert\mathbf{x}+\delta\mathbf{x}\Vert\le\frac{1}{1-k}(\Vert\mathbf{x}\Vert+k\Vert\mathbf{x}\Vert)=\frac{1+k}{1-k}\Vert\mathbf{x}\Vert$

性质三 ： $\displaystyle\frac{\Vert\delta\mathbf{x}\Vert}{\Vert\mathbf{x}\Vert}\le\frac{2\epsilon}{1-k}\kappa(A)$

性质二的关系式可写为 $\delta\mathbf{x}=A^{-1}(\delta\mathbf{b})-A^{-1}(\delta A)(\mathbf{x}+\delta\mathbf{x})$ ，计算 $\delta\mathbf{x}$ 长度：

$\Vert\delta\mathbf{x}\Vert\le\Vert A^{-1}\Vert\cdot\Vert\delta\mathbf{b}-(\delta A)(\mathbf{x}+\delta\mathbf{x})\Vert$

利用已知条件与三角不等式，可得

$\Vert\delta\mathbf{x}\Vert\le\epsilon\Vert A^{-1}\Vert\cdot\Vert\mathbf{b}\Vert+\epsilon\Vert A^{-1}\Vert\cdot\Vert A\Vert\cdot\Vert\mathbf{x}+\delta\mathbf{x}\Vert$

将上式除以 $\Vert\mathbf{x}\Vert$ 并利用性质二，

$\displaystyle\frac{\Vert\delta\mathbf{x}\Vert}{\Vert\mathbf{x}\Vert}\le\epsilon\kappa(A)\frac{\Vert\mathbf{b}\Vert}{\Vert A\Vert\cdot\Vert\mathbf{x}\Vert}+\epsilon\kappa(A)\frac{\Vert\mathbf{x}+\delta\mathbf{x}\Vert}{\Vert\mathbf{x}\Vert}\le\epsilon\kappa(A)\left(1+\frac{1+k}{1-k}\right)=\frac{2\epsilon}{1-k}\kappa(A)$

方程解的相对误差来自 $A$ 和 $\mathbf{b}$ 的相对扰动量和 $2\epsilon$ ，条件数 $\kappa(A)$ 再将此误差放大。换句话说，执行数值计算时，因舍入误差而造成的方程解误差有两个来源：一是线性系统自身的敏感性，以 $\kappa(A)$ 表示，另一则是真实误差 $\delta A$ 和 $\delta\mathbf{b}$ 。当我们用LU 分解计算时，受限于电脑的精准度，实际得到的是近似矩阵 $\tilde{L}$ 和 $\tilde{U}$ ，因此无可避免地使用了错误矩阵 $A+\delta A=\tilde{L}\tilde{U}$ 。英国数学家威尔金森(James H. Wilkinson)证明部分轴元法(partial pivoting，见“ PA=LU分解 ”)确实能够有效控制 $\delta A$ ，故舍入误差的主要决定因素为系数矩阵的条件数。感谢威尔金森提供的定心丸，除非碰上病态系统，否则我们大可放心地使用高斯消去法。

本文参考：
Gene H. Golub, Charles F. Van Loan，Matrix Computations，2 ^nd ed.，1989。

____________________________________________________________

1. 病态系统

现在有线性系统： Ax = b，解方程

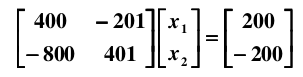
很容易得到解为： x1 = -100, x2 = -200. 如果在样本采集时存在一个微小的误差，比如，将 A 矩阵的系数 400 改变成 401：

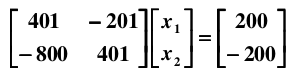
则得到一个截然不同的解： x1 = 40000, x2 = 79800.

当解集 x 对 A 和 b 的系数高度敏感，那么这样的方程组就是病态的 (ill-conditioned).

2. 条件数

那么，如何评价一个方程组是病态还是非病态的呢？在此之前，需要了解矩阵和向量的 norm，这里具体是计算很简单的 infinity norm，即找行绝对值之和最大，举个例子：

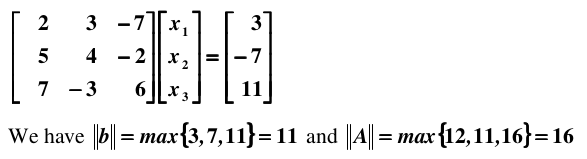
infinity norm 具有三角性质：||x+y|| <= ||x|| + ||y||. 理解了这些概念，下面讨论一下衡量方程组病态程度的条件数，首先假设向量 b 受到扰动，导致解集 x 产生偏差：

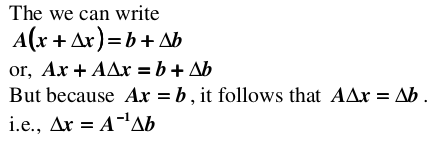
即有：

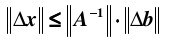
同时，由于

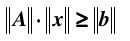
综合上面两个不等式：

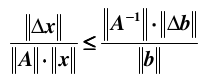
即得到最终的关系：

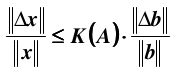
如果是矩阵 A 产生误差，同样可以得到：

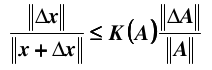
其中，条件数定义为：

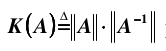
一般来说，方程组解集的精度大概是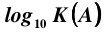个十进制的位的误差。比如，IEEE 标准表示的双精度浮点数的有效位是 16 位，如果条件数是 1e+10, 那么得到的结果中只有 6 位是精确的。所以，只有当方程组是良态时，残差 R = Ax - b 才能准确指示解的精度。

3. 病态的由来

自己的看法：

线性系统 Ax = b 为什么会病态？归根到底是由于 A 矩阵列向量线性相关性过大，表示的特征太过于相似以至于容易混淆所产生的。举个例子, 现有一个两个十分相似的列向量组成的矩阵 A：

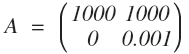
在二维空间上，这两个列向量夹角非常小。假设第一次检测得到数据 b = [1000, 0]^T, 这个点正好在第一个列向量所在的直线上，解集是 [1, 0]^T。现在再次检测，由于有轻微的误差，得到的检测数据是 b = [1000, 0.001]，这个点正好在第二个列向量所在的直线上，解集是 [0, 1]^T。两次求得到了差别迥异的的解集。

4. 与特征值和 SVD 的关系

特征值

假设 A 的两个单位特征向量是 x1, x2, 根据特征向量的性质：

$Ax_1 = \lambda _1x_1, Ax_2 = \lambda _2x_2$

上述矩阵 A 的特征值和特征向量分别为：

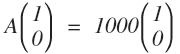
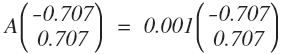
对于平面上的某一个向量 b，可以分解为两个特征向量的线性组合：

把上式带入， $b = mx_1 + nx_2 = \frac{m}{\lambda _1}\lambda _1x_1 + \frac{n}{\lambda _2}\lambda _2x_2 = A(\frac{m}{\lambda _1}x_1 + \frac{n}{\lambda _2}x_2) = Ax$

如果 $\lambda _1$ 远远大于 $\lambda _2$ ，当 b 点在 x1 方向发生移动, m 值改变，解集 x 变化不明显，反之，如果在 x2 方向移动， n 值改变，解集 x 变化非常大！可以看到，特征值对解集起到了一个 scaling 的作用。反过来说，如果一个特征值比其它特征值在数量级上小很多，x在对应特征向量 (x2) 方向上很大的移动才能产生b微小的变化.

2. SVD

SVD 分解：

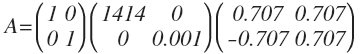
联系上次学到的 SVD 知识，将 A 分解成三个矩阵的乘积，中间的对角线矩阵也起到了 scaling 的作用。我们按照正向思维来考虑这个问题，现在来了一个解集 x 向量，左乘 A 矩阵等价与左乘 USV^T, x 向量正好等于 V^T 最后一行向量，经过 S 矩阵的 scaling 缩小之后对 b 的影响非常小。也就是说，解集 x 在 V^T 最后一行的行向量方向自由度最大！自由度越大，越不稳定，极端情况是该方向奇异值为 0, 解集可以在该方向取任意值，这也正好对应了矩阵 A 有零特征值， Ax 在对应特征向量的方向上移动不改变 Ax 的值。

在不同的 norm 下，条件数又可以由最大奇异值与最小奇异值之间的比值，或者最大特征值和最小特征值之间比值的绝对值来表示，详情请参考维基百科

最后， A 的条件数究竟等于多少呢？ cond(A) = 2e+06

5. 病态矩阵处理方法

真正的自由是建立在规范的基础上的。病态矩阵解集的不稳定性是由于解集空间包含了自由度过大的方向，解决这个问题的关键就是将这些方向去掉，而保留 scaling 较大的方向，从而把解集局限在一个较小的区域内。在上面的讨论中， A 矩阵的特征向量不一定正交，不适合做新基， SVD 分解正好分解出了正交基，可以选前 k 个 v^T 向量作为正交基。

比如，现在只选取前一个 (0.707, 0.707) 方向作为基，解集局限咋 y = x 这条直线上。直观的解释就是， A 矩阵的两个列向量过于类似，我们就可以将它们等同看待，第一次 b = (1000, 0), 解集是(0.5, 0.5), 第二次 b = (1000, 0.001), 解集还是 (0.5, 0.5).

总结起来，解决 A 病态就是将解集限定在一组正交基空间内，即对于坐标 y，选择 k 个正交基 Zk，解决问题：

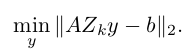
这个就是 reduce-rank model. 具体方法有 truncated SVD 和 Krylov subspace method。

参考资料：

(1) ILL-Conditioned Systems

作者：daniel-D 出处：http://www.cnblogs.com/daniel-D/ 欢迎转载或分享，但请务必声明文章出处。

分类: Mathematics

标签: matrix

赏月斋

慎终如始宁静致远

条件数

1. 病态系统

2. 条件数

3. 病态的由来

4. 与特征值和 SVD 的关系

5. 病态矩阵处理方法

公告

赏月斋

慎终如始 宁静致远

病态矩阵与条件数

条件数

1. 病态系统

2. 条件数

3. 病态的由来

4. 与特征值和 SVD 的关系

5. 病态矩阵处理方法

公告

慎终如始宁静致远