A Knight's Journey

                                      A Knight's Journey

                                                        Time Limit : 2000/1000ms (Java/Other)   Memory Limit : 131072/65536K (Java/Other

Problem Description

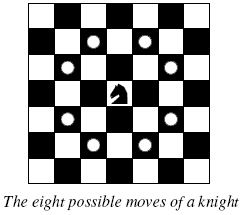Background 
The knight is getting bored of seeing the same black and white squares again and again and has decided to make a journey 
around the world. Whenever a knight moves, it is two squares in one direction and one square perpendicular to this. The world of a knight is the chessboard he is living on. Our knight lives on a chessboard that has a smaller area than a regular 8 * 8 board, but it is still rectangular. Can you help this adventurous knight to make travel plans? 

Problem 
Find a path such that the knight visits every square once. The knight can start and end on any square of the board.

 

Input

The input begins with a positive integer n in the first line. The following lines contain n test cases. Each test case consists of a single line with two positive integers p and q, such that 1 <= p * q <= 26. This represents a p * q chessboard, where p describes how many different square numbers 1, . . . , p exist, q describes how many different square letters exist. These are the first q letters of the Latin alphabet: A, . . .

 

Output

The output for every scenario begins with a line containing "Scenario #i:", where i is the number of the scenario starting at 1. Then print a single line containing the lexicographically first path that visits all squares of the chessboard with knight moves followed by an empty line. The path should be given on a single line by concatenating the names of the visited squares. Each square name consists of a capital letter followed by a number. 
If no such path exist, you should output impossible on a single line.

 

Sample Input

3

1 1

2 3

4 3

 

Sample Output

Scenario #1:

A1

 

 

Scenario #2:

impossible

 

Scenario #3:

A1B3C1A2B4C2A3B1C3A4B2C4

 

题意：问在给的p*q的棋盘上，以象棋中马的行走方式，是否可以不重复的走完整个棋盘。若可以则输出任意一种行走方式，注意要按照字典序的方式输出。不可以就输出“impossible”。

 思路，用的深搜dfs  在当前位置像其他地方搜索，顺着一个叉继续向下搜，成功则输出，不成功就返回。具体看代码的注释

源代码：

#include<iostream>
using namespace std;
const int Max=25;
bool visit[Max][Max] , output;
int visitnum ,p,q;  //总的要走的步数，棋盘的行列
char pa[2*Max];     //记录走的位置，每两个表示一个位置
int dx[8]={-2,-2,-1,-1,1,1,2,2};
int dy[8]={-1,1,-2,2,-2,2,-1,1};              //按字典序的顺序。
void dfs(int depth,int x,int y)               //depth表示第几步，x，y表示马当前所在的位置。
{
    if(depth==visitnum)                      //表示全部访问 
    {
        for(int i=0;i<2*depth;i++)            //输出结果
            cout<<pa[i];
        cout<<endl<<endl;
        output=true;
        return ;
    }
    for(int i=0;i<8 && output==false ;i++)   // 向八个方向搜索
        {
            int newx=x+dx[i];
            int newy=y+dy[i];
            if(newx>0 && newy>0 && newx<=q && newy<=p && visit[newy][newx] == false)  //在棋盘内且未访问过则访问
            {
                visit[newy][newx]=true;
                pa[2*depth]='A'+newx-1;   //记录行的位置
                pa[2*depth+1]='1'+newy-1; //记录列的位置
                dfs(depth+1,newx,newy);   //走的步数+1 继续向下搜
                visit[newy][newx]=false;  //为其余搜索的情况置初值
            }
        }
}
int main()
{
    int n;
    cin>>n;
    for(int i=1;i<=n;i++)
    {
        cin>>p>>q;
        cout<<"Scenario #"<<i<<":"<<endl;  
        for(int y=1;y<=p;y++)        //输入
            for(int x=1;x<=q;x++)
               visit[y][x]=false;
        visitnum=p*q;              //总的步数  
        output=false;              //output表示搜索完成情况
        visit[1][1]=true;
        pa[1]='1';
        pa[0]='A';           //初始位置，因为只要能走完，那么完全可以在（A，1）处开始移动
        dfs(1,1,1);
        if(output==false)
            cout<<"impossible"<<endl<<endl;
    }
    return 0;
}