Radar Installation
Radar Installation
Time Limit : 2000/1000ms (Java/Other) Memory Limit : 20000/10000K (Java/Other)
Problem Description
Assume the coasting is an infinite straight line. Land is in one side of coasting, sea in the other. Each small island is a point locating in the sea side. And any radar installation, locating on the coasting, can only cover d distance, so an island in the sea can be covered by a radius installation, if the distance between them is at most d.
We use Cartesian coordinate system, defining the coasting is the x-axis. The sea side is above x-axis, and the land side below. Given the position of each island in the sea, and given the distance of the coverage of the radar installation, your task is to write a program to find the minimal number of radar installations to cover all the islands. Note that the position of an island is represented by its x-y coordinates.
![]()
Figure A Sample Input of Radar Installations
We use Cartesian coordinate system, defining the coasting is the x-axis. The sea side is above x-axis, and the land side below. Given the position of each island in the sea, and given the distance of the coverage of the radar installation, your task is to write a program to find the minimal number of radar installations to cover all the islands. Note that the position of an island is represented by its x-y coordinates.
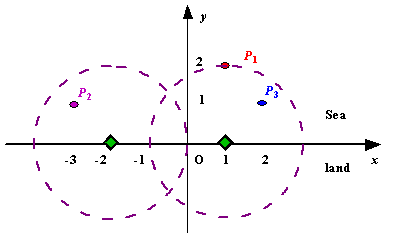
Figure A Sample Input of Radar Installations
Input
The input consists of several test cases. The first line of each case contains two integers n (1<=n<=1000) and d, where n is the number of islands in the sea and d is the distance of coverage of the radar installation. This is followed by n lines each containing two integers representing the coordinate of the position of each island. Then a blank line follows to separate the cases.
The input is terminated by a line containing pair of zeros
The input is terminated by a line containing pair of zeros
Output
For each test case output one line consisting of the test case number followed by the minimal number of radar installations needed. "-1" installation means no solution for that case.
Sample Input
3 2
1 2
-3 1
2 1
1 2
0 2
0 0
Sample Output
Case 1: 2
Case 2: 1
题意:p 点表示 岛屿,x轴是海岸线,在轴上建立雷达装置,d 表示每个装置的覆盖半径, 问最少需要多少雷达装置可以把所有的岛屿覆盖,如果有无法覆盖的就输出“-1”;
思路:先计算出在x轴上能覆盖每个岛屿的范围(L,R),然后以 L 排序,最后根据 条件排序即可;详见代码;
源代码:
#include<iostream> #include<cmath> #include<algorithm> using namespace std; const int maxn=1005; struct Line { double l,r; }line[maxn]; bool cmp(Line a,Line b) { return a.l<b.l; } int main() { int n,d; int x,y,i; bool yn; int icase=1; while(cin>>n>>d) { yn=true; int c=0; if(n==0&&d==0) break; for(i=0;i<n;i++) { cin>>x>>y; if(yn==false) continue; if(y>d) yn=false; else { line[i].l=(double)x-sqrt((double)d*d-y*y); line[i].r=(double)x+sqrt((double)d*d-y*y); } } if(yn==false) { cout<<"Case "<<icase++<<": -1"<<endl; continue; } sort(line,line+n,cmp); c++; double now=line[0].r; for(i=1;i<n;i++) ///计算条件 { if(line[i].r<now) now=line[i].r; ///这点很重要!容易忘 else if(now<line[i].l) ///关键条件 { now=line[i].r; c++; } } cout<<"Case "<<icase++<<": "<<c<<endl; } return 0; }
书山有路勤为径,学海无涯苦作舟!!!



 浙公网安备 33010602011771号
浙公网安备 33010602011771号