深度学习第二节——深度学习概述

神经网络基础

1.浅层神经网络

一、生物神经元与神经网络相关的部分

　　1.每个神经元都是一个多输入单输出的信息处理单元；

　　2.神经元具有空间整合和时间整合特性；

　　3.神经元输入分兴奋性输入和抑制性输入两种类型；

　　4.神经元具有阈值特性。

二、M-P神经元（对生物神经元的抽象和简化）

　　

　　 

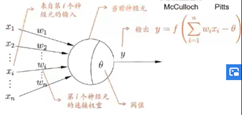
三、激活函数

         1.为什么需要激活函数？

　　·神经元继续传递信息、产生新连接的概率（超过阈值被激活，但不一定传递）

　　·没有激活函数相当于矩阵相乘：多层和一层一样，只能拟合线性函数

　　

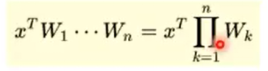
　　2.常见的激活函数举例：

　　

 

 　　

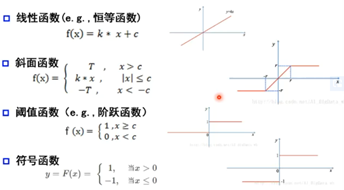
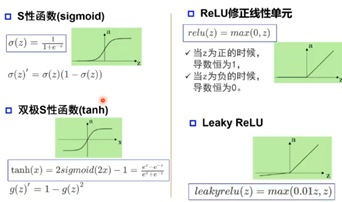
　　·S性函数(sigmoid) （早期应用，容易饱和，输出不对称）

　　饱和区问题：当输入太大或太小时，斜率非常小

　　·双极S性函数(tanh)  

　　·ReLU修正线性单元 （最大值，解决饱和区问题，输入为负不会得到正值）

　　·Leaky ReLU

四、单层感知器

　　·M-P神经元的权重预先设置，无法学习

　　·单层感知器是首个可以学习的人工神经网络

　　

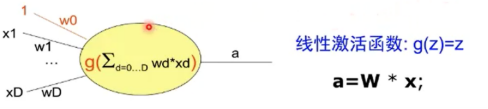
　　单层感知器怎么实现逻辑功能？举例

　　

　　1.逻辑非的实现

　　

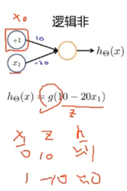
　　2.逻辑或

　　

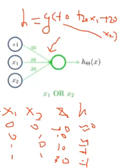
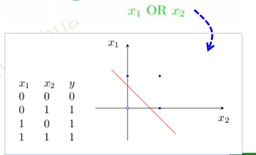
　　3.逻辑与

　　

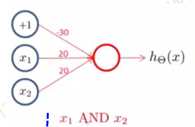
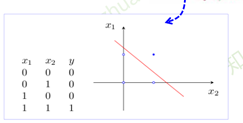
　　单层感知器能实现一些简单与非或问题，但是非线性问题呢？（如异或）

　　单层->多层感知器（可以证明单层感知器无法解决异或问题）

　　可以将异或问题转化为简单的逻辑电路问题，既可以通过多层感知器来解决这个问题。

五、万有逼近定理

　　如果一个隐层包含足够多的神经元，三层前馈神经网络（输入-隐层-输出）能以任意精度逼近任意预定的连续函数。

　　为什么线性分类任务组合后可以解决非线性分类任务？

　　可以理解为第一层感知器做的是空间的变化（运用线性代数相关知识）类似于加入变换后的支持向量机。

　　·双隐层感知器逼近非连续函数

　　当隐层足够宽时，双隐层感知器（输入-隐层1-隐层2-输出）可以逼近任意非连续函数：可以解决任何复杂的分类问题。

 　　

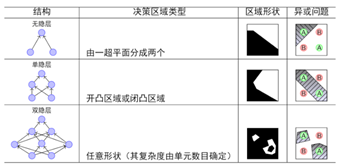
六、神经网络每一层的作用

 　　

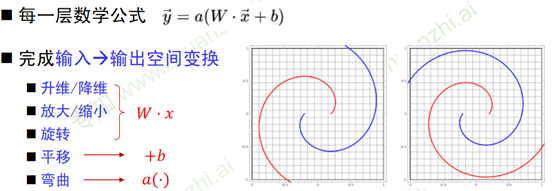
　　Demo：https://cs.stanford.edu/people/karpathy/convnetjs//demo/classify2d.html

1. 神经网络学习如何利用矩阵的线性变换加激活函数的非线性变换，将原始输入空间投影到线性可分的空间去分类/回归。
2. 增加节点数：增加维度，即增加线性转换能力。
3. 增加层数：增加激活函数的次数，即增加非线性

　　神经网络的参数学习：误差反向传播

　　·多层神经网络可看成是一个复合的非线性多元函数 F(⋅):𝑋 → 𝑌

　　·给定训练数据 x i , y i i=1:N，希望损失 𝑖 𝑙𝑜𝑠𝑠(𝐹 𝑥 𝑖 , 𝑦 𝑖 )尽可能小

七、更宽or更深

　　

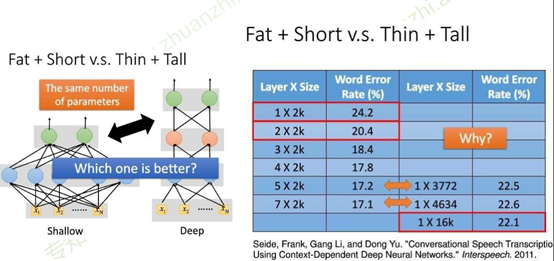
　　结点可以理解为成本，相同结点数时，左边瘦高的网络错误率比右边矮胖的网络低。（16K个结点时，17.1对22.1）

　　更宽还是更深？更深！

1. 在神经元总数相当的情况下，增加网络深度可以比增加宽度带来更强的网络表示能力：产生更多的线性区域[1]。 [1] On the Number of Linear Regions of Deep Neural Networks.
2. 深度和宽度对函数复杂度的贡献是不同的，深度的贡献是指数增长的，而宽度的贡献是线性的[2]。[2] Delalleauand Y. Bengio. Shallow vs. deep sum-product networks. In NIPS, 201

　　那是不是把网络往深度加就可以了？

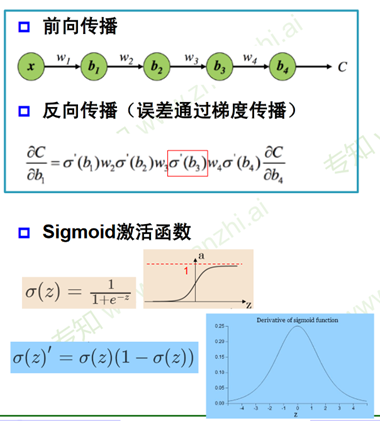
　　多层神经网络的问题：梯度消失？

　　先讲神经网络的参数学习：误差反向传播

 　　

 　　

　　

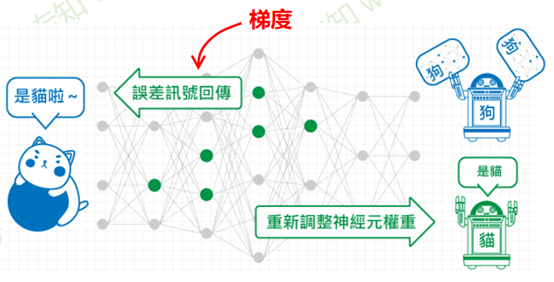
梯度和梯度下降

 

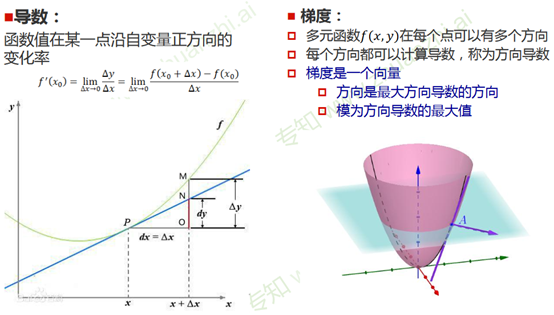
1.为什么沿着这个方向可以使函数值下降：利用泰勒公式

2.对于凸函数只有一个极值点，非凸函数非常依赖初始值的选择。

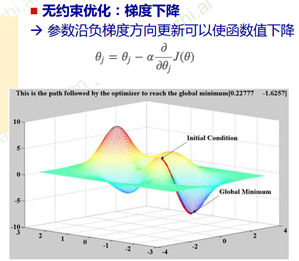
　　神经网络的参数学习：误差反向传播

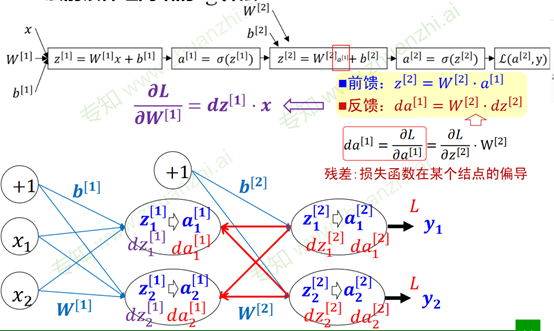
　　复合函数的链式求导

 

 　　

　　三层前馈神经网络的BP算法

　　

　　深度学习开发框架（pyTorch）

　　多层神经网络的问题：梯度消失？

　　2. 从神经网络到深度学习