PTA山峰形状

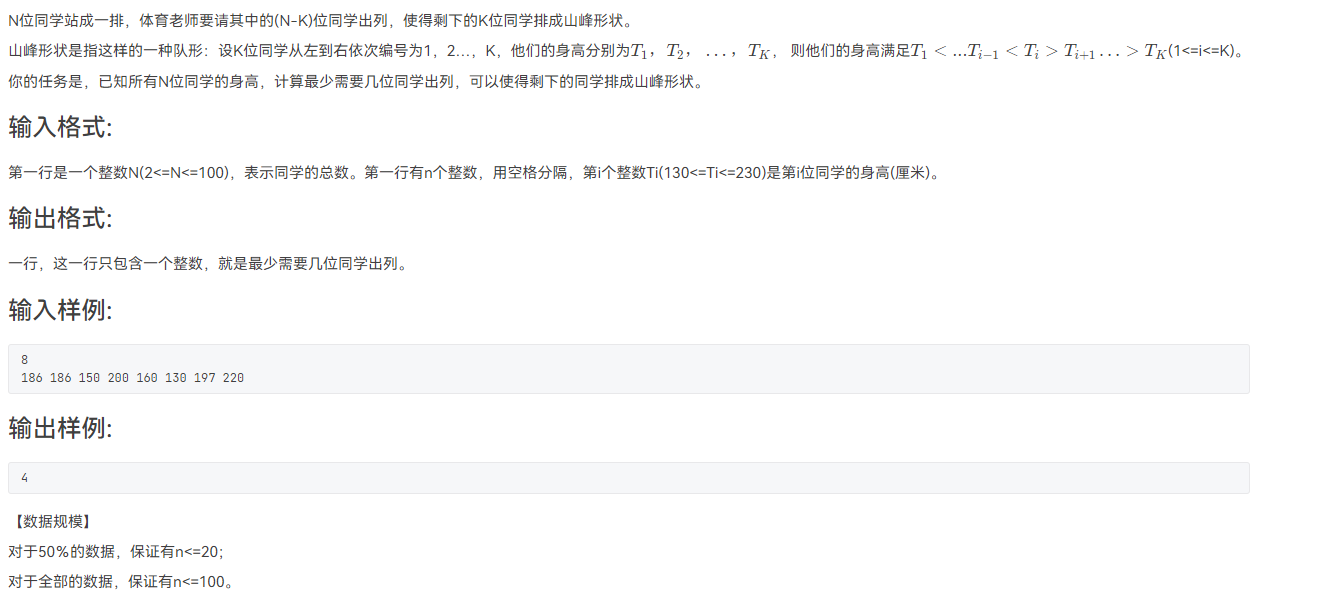
一、题目描述

 

 

 二、解题思路

　　这题其实就是枚举每个位置，然后根据这个位置判断需要剔除几个人，反向思考，我们需要剔除几个人。

　　pos之前的部分做一个最长递增子序列的dp，用前面的总人数减去最长递增就是前面部分需要剔除几个人

　　pos之后的部分做一个最长递减子序列的dp，用前面的总人数减去最长递减就是后面部分需要剔除几个人

　　然后比较一下，最小剔除人数，记录位置就可以了

三、代码实现

 1 #include "bits/stdc++.h"
 2 #define PII pair<int,int>
 3 #define rep(i,z,n) for(int i = z;i <= n; i++)
 4 #define per(i,n,z) for(int i = n;i >= z; i--)
 5 #define ll long long
 6 #define db double
 7 #define vi vector<int>
 8 #define debug(x) cerr << "!!!" << x << endl;
 9 using namespace std;
10 //从某个串中把某个子串替换成另一个子串
11 string& replace_all(string& src, const string& old_value, const string& new_value) {
12     // 每次重新定位起始位置，防止上轮替换后的字符串形成新的old_value
13     for (string::size_type pos(0); pos != string::npos; pos += new_value.length()) {
14         if ((pos = src.find(old_value, pos)) != string::npos) {
15             src.replace(pos, old_value.length(), new_value);
16         }
17         else break;
18     }
19     return src;
20 }
21 inline ll read()
22 {
23     ll s,r;
24     r = 1;
25     s = 0;
26     char ch = getchar();
27     while(ch < '0' || ch > '9'){
28         if(ch == '-')
29             r = -1;
30         ch = getchar();
31     }
32     while(ch >= '0' && ch <= '9'){
33         s = (s << 1) + (s << 3) + (ch ^ 48);
34         ch = getchar();
35     }
36     return s * r;
37 }
38 inline void write(ll x)
39 {
40     if(x < 0) putchar('-'),x = -x;
41     if(x > 9) write(x / 10);
42     putchar(x % 10 + '0');
43 }
44 int a[110];
45 int n;
46 int solve(int pos)
47 {
48     int ans = 0;
49     int dp1[110];
50     int dp2[110];
51     // cout << pos << ',';
52     for(int i = 1;i <= n;i++)
53         dp1[i] = dp2[i] = 1;
54     for(int i = 1;i < pos;i++)
55         for(int j = i + 1;j <= pos;j++)
56             if(a[j] > a[i])
57                 dp1[j] = max(dp1[j],dp1[i] + 1);
58     int mx = -INT_MAX;
59     for(int i = 1;i <= pos;i++)
60         mx = max(mx,dp1[i]);
61     ans += pos - mx;
62     // cout << mx << ' ,';
63     for(int i = pos;i < n;i++)
64         for(int j = i + 1;j <= n;j++)
65             if(a[j] < a[i])
66                 dp2[j] = max(dp2[j],dp2[i] + 1);
67     mx = -INT_MAX;
68     for(int i = pos;i <= n;i++)
69         mx = max(dp2[i],mx);
70     // cout << mx << endl;
71     ans += (n - pos + 1) - mx; 
72     return ans;
73 }
74 int main()
75 {
76     
77     n = read();
78     rep(i,1,n)
79         cin >> a[i];
80     int ans = INT_MAX;
81     rep(i,1,n){
82         if(ans > solve(i))
83             ans = solve(i);
84     }
85     cout << ans;
86     return 0;
87 }
posted @ 2022-03-23 21:51  scannerkk  阅读(46)  评论(0)    收藏  举报