PTA印章

一、题目描述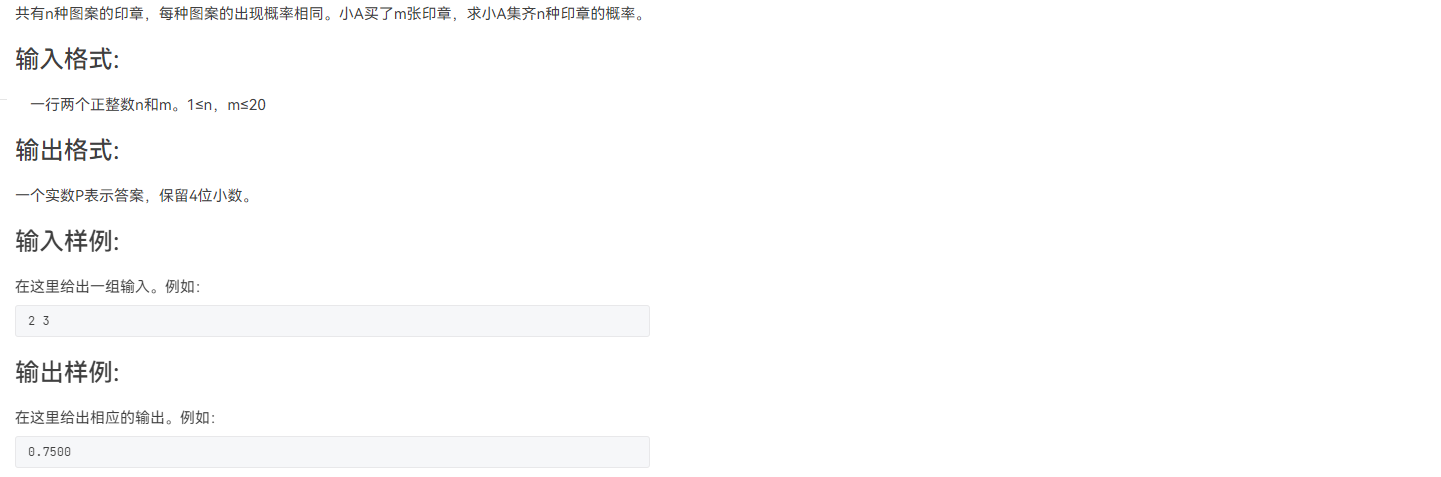

 

 二、解题思路

　　这题是一个概率DP题，我们考虑三种情况

　　我们用dp[i][j]代表i张印章能凑出j种，设p = 1 / n

　　

　　显然第一种情况

　　　　当i<j时，dp[i][j]=0，因为不可能凑出j种

　　第二种情况

　　　　当j = 1时，此时选出的i张里面都是某一种，概率是(p^i)，又因为可能都是n中的同一种，故都需要乘上n，因此概率为(p^(i-1))

　　第三种情况

　　　　当不处于上述两种情况时

　　　　　　如果此时前i - 1张，凑出了j 种印章，但是我现在拿到的和前j种重复了，此时的概率为(j / n)

　　　　　　如果此时前i - 1张，凑出了j - 1种印章，但是我现在拿到不属于前j - 1种的概率是(n - j + 1) / n

　　故可以写出状态转移方程

 

　　if(i < j) dp[i][j] = 0;

　　else if(j == 1) dp[i][j] = pow(p,i - 1);

　　else dp[i][j] = dp[i - 1][j] * (j * 1.0 / n) + dp[i - 1][j - 1] * ((n - j + 1) * 1.0 / n);

三、代码实现

#include "bits/stdc++.h"
#define PII pair<int,int>
#define rep(i,z,n) for(int i = z;i <= n; i++)
#define per(i,n,z) for(int i = n;i >= z; i--)
#define ll long long
#define db double
#define vi vector<int>
#define debug(x) cerr << "!!!" << x << endl;
using namespace std;
//从某个串中把某个子串替换成另一个子串
string& replace_all(string& src, const string& old_value, const string& new_value) {
    // 每次重新定位起始位置，防止上轮替换后的字符串形成新的old_value
    for (string::size_type pos(0); pos != string::npos; pos += new_value.length()) {
        if ((pos = src.find(old_value, pos)) != string::npos) {
            src.replace(pos, old_value.length(), new_value);
        }
        else break;
    }
    return src;
}
inline ll read()
{
    ll s,r;
    r = 1;
    s = 0;
    char ch = getchar();
    while(ch < '0' || ch > '9'){
        if(ch == '-')
            r = -1;
        ch = getchar();
    }
    while(ch >= '0' && ch <= '9'){
        s = (s << 1) + (s << 3) + (ch ^ 48);
        ch = getchar();
    }
    return s * r;
}
inline void write(ll x)
{
    if(x < 0) putchar('-'),x = -x;
    if(x > 9) write(x / 10);
    putchar(x % 10 + '0');
}
double dp[30][30];
int main()
{
    int n,m;
    n = read();
    m = read();
    double p = 1.0 / n;
    for(int i = 1;i <= m;i++){
        for(int j = 1;j <= n;j++){
            //如果i<j,说明此时i张印章一定不能凑出j种印章
            if(i < j) dp[i][j] = 0;
            //如果j==1,此时选出的i张里面都是某一种，概率是(p^i)，又因为可能都是n中的同一种，故都需要乘上n，因此概率为(p^(i-1))
            else if(j == 1) dp[i][j] = pow(p,i - 1);
            //如果当前选的和之前选出的j种是同一种，那么此时的概率为(j / n),因为n中里面选出前j种的概率为(j / n)
            //如果当前选的和之前的不同，说明增加了一种，此时前面选了j - 1种，我们不选到前面j - 1种的概率为(n -(j - 1)) / n = (n - j + 1) / n
            else dp[i][j] = dp[i - 1][j] * (j * 1.0 / n) + dp[i - 1][j - 1] * ((n - j + 1) * 1.0 / n);
        }
    }
    cout << fixed << setprecision(4) << dp[m][n];
    return 0;
}