CFedu124A-C

 

 

 

 

 

 解题思路

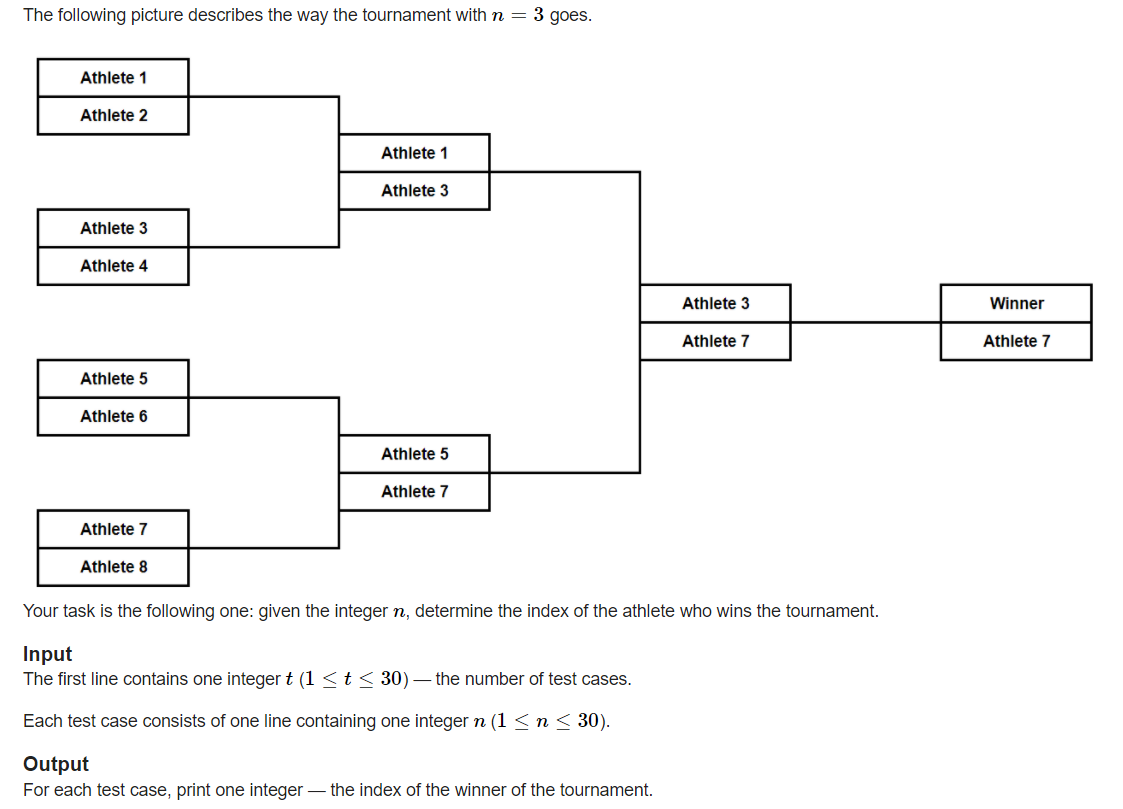
　　很容易看出来这两个操作最后的赢者一定是2^n - 1,故直接输出2^n - 1就是答案

代码实现

 1 #include "bits/stdc++.h"
 2 #define PII pair<int,int>
 3 #define rep(i,z,n) for(int i = z;i <= n; i++)
 4 #define per(i,n,z) for(int i = n;i >= z; i--)
 5 #define ll long long
 6 #define db double
 7 #define vi vector<int>
 8 #define debug(x) cerr << "!!!" << x << endl;
 9 using namespace std;
10 inline ll read()
11 {
12     ll s,r;
13     r = 1;
14     s = 0;
15     char ch = getchar();
16     while(ch < '0' || ch > '9'){
17         if(ch == '-')
18             r = -1;
19         ch = getchar();
20     }
21     while(ch >= '0' && ch <= '9'){
22         s = (s << 1) + (s << 3) + (ch ^ 48);
23         ch = getchar();
24     }
25     return s * r;
26 }
27 inline void write(ll x)
28 {
29     if(x < 0) putchar('-'),x = -x;
30     if(x > 9) write(x / 10);
31     putchar(x % 10 + '0');
32 }
33 int main()
34 {
35     int n;
36     int t;
37     cin >> t;
38     while(t--){
39         n = read();
40         cout << (2 << (n - 1)) - 1 << endl;    
41     }
42     return 0;
43 }

 

 

 

 

 

 

 

解题思路：

　　这个题类似于构造题，要想明白这个长度为n的数组如何构造才能达到做这个操作后不减得操作。把公式化简一下，移项就可以得到一个3倍的关系，故从1开始后面那个数就是前面那个数的三倍，如果超过了1e9就结束循环，然后判断答案的个数就可以了，复杂度为O(logn)。

代码实现

 1 #include "bits/stdc++.h"
 2 #define PII pair<int,int>
 3 #define rep(i,z,n) for(int i = z;i <= n; i++)
 4 #define per(i,n,z) for(int i = n;i >= z; i--)
 5 #define ll long long
 6 #define db double
 7 #define vi vector<int>
 8 #define debug(x) cerr << "!!!" << x << endl;
 9 using namespace std;
10 inline ll read()
11 {
12     ll s,r;
13     r = 1;
14     s = 0;
15     char ch = getchar();
16     while(ch < '0' || ch > '9'){
17         if(ch == '-')
18             r = -1;
19         ch = getchar();
20     }
21     while(ch >= '0' && ch <= '9'){
22         s = (s << 1) + (s << 3) + (ch ^ 48);
23         ch = getchar();
24     }
25     return s * r;
26 }
27 inline void write(ll x)
28 {
29     if(x < 0) putchar('-'),x = -x;
30     if(x > 9) write(x / 10);
31     putchar(x % 10 + '0');
32 }
33 int dp = 1;
34 int limit = 1e9;
35 int main()
36 {
37     int t;
38     cin >> t;
39     while(t--){
40         int n;
41         n = read();
42         vector <long long> ans;
43         int nums = 0;
44         dp = 1;
45         while(1){
46             if(dp <= limit)
47                 ans.push_back(dp);
48             nums++;
49             dp = dp * 3 + 1;
50             if(dp > limit)
51                 break;
52             if(nums == n)
53                 break;
54         }
55         int len = ans.size();
56         if(len < n)
57             cout << "NO" << endl;
58         else {
59             cout << "YES" << endl;
60             for(auto u:ans)
61                 cout << u << ' ';
62             cout << endl;
63         }
64     }
65     return 0;
66 }

 

 

 解题思路：

　　我们可以尝试一下如果有任何一个点被去除了，还要保证这个网络是连通的话，我们必须要把四个端点进行连通。

　　

　　这四个端点进行连通的话就会有三种情况

　　第一种：两条线

　　　　　　两条线可以是a[1] 和 b[1] 然后 a[n] 和 b[n]

　　　　　　也可以是a[1] 和 b[n] 然后 a[n] 和 b[1]

　　第二种：三条线

　　　　　　一共有八种情况

　　第三种：四条线

　　　　　　一共只有一种情况

　　　　　　就是任意一个点连接另一边的两个顶点，比如说a[2] 连接 b[1] 和 b[n] ，然后 b[3] 连接 a[1] 和 a[n]

　　可以直接用循环暴力枚举所有情况就可以了

 

代码实现：

 1 #include "bits/stdc++.h"
 2 #define PII pair<int,int>
 3 #define rep(i,z,n) for(int i = z;i <= n; i++)
 4 #define per(i,n,z) for(int i = n;i >= z; i--)
 5 #define ll long long
 6 #define db double
 7 #define vi vector<int>
 8 #define debug(x) cerr << "!!!" << x << endl;
 9 using namespace std;
10 inline ll read()
11 {
12     ll s,r;
13     r = 1;
14     s = 0;
15     char ch = getchar();
16     while(ch < '0' || ch > '9'){
17         if(ch == '-')
18             r = -1;
19         ch = getchar();
20     }
21     while(ch >= '0' && ch <= '9'){
22         s = (s << 1) + (s << 3) + (ch ^ 48);
23         ch = getchar();
24     }
25     return s * r;
26 }
27 inline void write(ll x)
28 {
29     if(x < 0) putchar('-'),x = -x;
30     if(x > 9) write(x / 10);
31     putchar(x % 10 + '0');
32 }
33 long long a[200010],b[200010];
34 int main()
35 {
36     int t;
37     t = read();
38     while(t--){
39         int n;
40         n = read();
41         rep(i,1,n)
42             a[i] = read();
43         rep(i,1,n)
44             b[i] = read();
45         long long ans1,ans2,ans3,ans4;
46         ans1 = ans2 = ans3 = ans4 = INT_MAX;
47         rep(i,1,n){
48             ans1 = min(ans1,abs(a[i] - b[1]));
49             ans2 = min(ans2,abs(b[i] - a[1]));
50             ans3 = min(ans3,abs(b[n] - a[i]));
51             ans4 = min(ans4,abs(a[n] - b[i]));
52         }
53         cout << min((min((ans1 + ans2),abs(a[1] - b[1])) + min(ans3 + ans4,abs(a[n] - b[n]))),
54                     min(abs(a[1] - b[n]),ans2 + ans3) + min(abs(a[n] - b[1]),ans1 + ans4)) << endl;
55     }
56     return 0;
57 }
posted @ 2022-03-12 13:07  scannerkk  阅读(20)  评论(0)    收藏  举报