Bellman-Ford和SPFA(队列优化的Bellman-Ford)

一、Bellman-Ford算法

　　1.定义

　　　　Bellman-Ford 算法是一种用于计算带权有向图中单源最短路径，它和Dijkstra的不同点是，它能计算带有负权边的最短路，而Dijkstra不能计算，而且它能判断负环的出现。

　　2.实现

　　　　先看张图（小圈为边的编号）

　　　　　

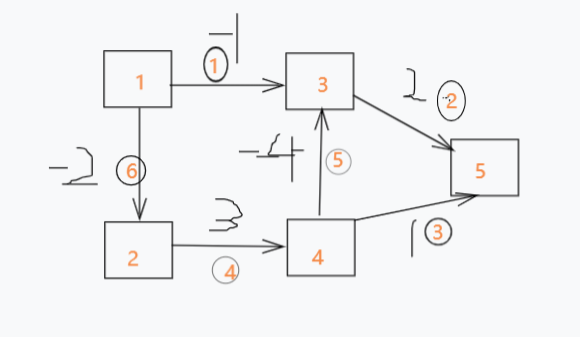
 　　　　我要从1到5

　　　　　　1.首先初始化dis数组(inf代表无穷大)

　　　　　　　

 

 

 

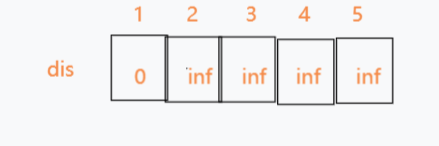
 　　　　　　2.从第一条边开始从松弛每一个顶点到源点的距离

　　　　　　　　第一条边是1->3

　　　　　　　　看看能否通过这条边松弛3号点到源点的距离，发先dis[3] > dis[1] + 1->3边权

　　　　　　　　所以更新dis[3]为-1

 

　　　　　　　　　　

 

 

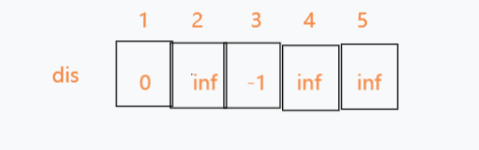
 　　　　　　3.从第二条边开始继续尝试3->5发现可以松弛5，于是乎dis[5] = dis[3] + 3->5 = 1

　　　　　　　　　　

 

 

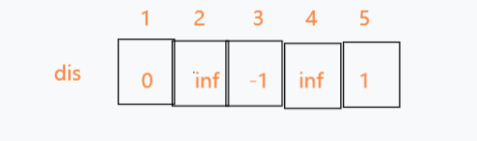
 　　　　　　4.从第三条边开始尝试4->5，发现不能松弛，故不更新dis[5]

　　　　　　　　　　

 

 

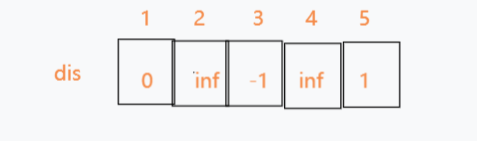
 　　　　　　5.从第四条边开始尝试2->4，发现不能松弛4，故dis[4]不更新

　　　　　　　　　　

 

 

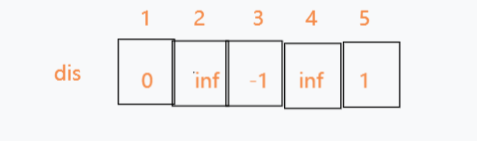
 　　　　　　6.从第五条边开始继续尝试4->3，发现不能松弛3，故dis[3]不更新

　　　　　　　　　　

 

 

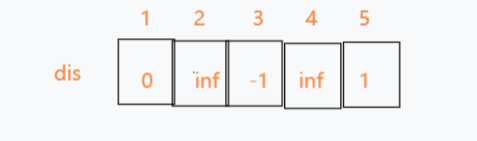
 　　　　　　7.从第六条边开始尝试1->2，发现可以松弛2，故更新dis[2]为-1

　　　　　　　　　　

 

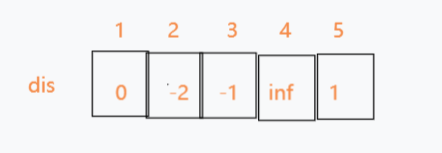
 　　　　　　这是第一轮的松弛，最多可以松弛n-1轮就可以找到最短路径了。(为什么只需要n-1轮，因为n个点的单源最短路径最多只能有n-1条边，所以松弛n-1次就一定是最多路径了)

　　　　　　8.最后结果为

　　　　　　　　　　

 

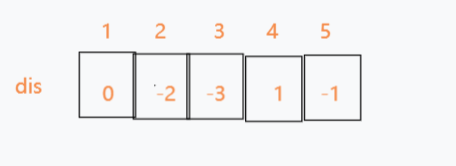
　　　　判断负环就是在执行为n - 1次的松弛操作后，发现还可以松弛，这肯定就有负环了。

 　　　　3.代码

 1 #include "bits/stdc++.h"
 2 using namespace std;
 3 const int inf = 1e9 + 10;
 4 int n,m;
 5 int pre[110],dis[110];
 6 int cnt;
 7 struct node{
 8     int from;
 9     int to;
10     int weight;
11 }edges[110];
12 void add(int u,int v,int w)
13 {
14     edges[++cnt].from = u;
15     edges[cnt].to = v;
16     edges[cnt].weight = w;
17 }
18 void initRoad()
19 {
20     for(int i = 1;i <= n;i++)
21         pre[i] = -1;
22     for(int i = 2;i <= n;i++)
23         dis[i] = inf;
24 }
25 void printRoad(int u)
26 {
27     if(u == -1)
28         return;
29     printRoad(pre[u]);
30     cout << u << endl;
31 }
32 bool BellmanFord()
33 {
34     for(int i = 1;i <= n;i++)
35         for(int j = 1;j <= cnt;j++)
36             if(dis[edges[j].to] > dis[edges[j].from] + edges[j].weight){
37                 dis[edges[j].to] = dis[edges[j].from] + edges[j].weight;
38                 pre[edges[j].to] = edges[j].from;
39             }
40     bool ok = false;
41     for(int i = 1;i <= cnt;i++)
42         if(dis[edges[i].to] > dis[edges[i].from] + edges[i].weight)
43             ok = true;
44     return ok;
45 }
46 int main()
47 {
48     cin >> n >> m;
49     initRoad();
50     for(int i = 1;i <= m;i++){
51         int u,v,w;
52         cin >> u >> v >> w;
53         add(u,v,w);
54     }
55     //有负环
56     if(BellmanFord())
57         cout << "Has negative ring!";
58     //输出路径
59     else {
60         cout << '1' << endl;
61         printRoad(n);
62         cout << "weight:" << endl;
63         for(int i = 1;i <= n;i++)
64             cout << dis[i] << ' ';
65     }
66     //test case(无环)
67     // 4 5
68     // 1 2 4
69     // 2 4 -1
70     // 2 3 -2
71     // 3 4 0
72     // 4 2 2
73 
74     //test case(有环)
75     // 4 5
76     // 1 2 -2
77     // 2 3 -2
78     // 2 4 1 
79     // 3 4 0
80     // 4 1 0
81     return 0;
82 }

二、SPFA

　　Bellman-Ford的复杂度计算可知为O(v * e)，复杂度比较高了。此时我们能不能优化一下呢？答案是可以的。我们会发现遍历边的时候有些边是松弛不了的，但是我们还需要去判断是否可以松弛，那么我们怎样可以减少这个判断呢？我们可以知道如果一点的路径缩短了，那么他的出边的路径很可能会被缩短（为什么说是很可能，而不是一定呢？因为可能这个出边的那个点被其他的边松弛了），所以我们就需要走一下这个顶点的出边，那么我们就可以用到队列来做了，如果一个点的路径被松弛了，我们判断他是否在队列中，如果不在那么我们就把这个点进行入队。判断负环的话可以设置一个cnt数组，记录被松弛的次数，如果到了n次，说明出现了负环。(源点到from的最短路径所含的边数等于源点到to的最短路径所含的边数+1)

　　cnt数组记录每个点到源点的距离被更新的次数，当某点到源点的距离被更新的次数大于等于n时就说明存在负环。

　　代码实现

 1 #include "bits/stdc++.h"
 2 using namespace std;
 3 const int inf = 1e9;
 4 int inq[10010];//inq数组判断该点是否处于队列中
 5 int dis[10010];//dis数组用来存距离
 6 int vis[10010];//vis数组用来判断是否存在负环
 7 int heads[10010];//heads数组用来存第一个该点出现的下标
 8 struct node{
 9     int to;
10     int nxt;
11     int w;
12 }edges[10010];
13 int n,m;
14 int cnt;
15 //在边集数组中加边
16 void add(int u,int v,int w)
17 {
18     edges[++cnt].to = v;
19     edges[cnt].w = w;
20     edges[cnt].nxt = heads[u];
21     heads[u] = cnt;
22 }
23 //初始化
24 void init()
25 {
26     for(int i = 1;i <= n;i++)
27         inq[i] = false;
28     for(int i = 1;i <= n;i++)
29         dis[i] = inf;
30     for(int i = 1;i <= n;i++)
31         vis[i] = 0;
32     for(int i = 1;i <= n;i++)
33         heads[i] = -1;
34 }
35 void spfa(int s)
36 {
37     dis[s] = 0;
38     inq[s] = true;
39     cnt[s] = 1;
40     queue <int> que;
41     que.push(s);
42     while(!que.empty()){
43         int v = que.front();
44         que.pop();
45         inq[v] = false;
46         for(int i = heads[v];i != -1;i = edges[i].nxt){
47             if(dis[edges[i].to] > dis[v] + edges[i].w){
48                 dis[edges[i].to] = dis[v] + edges[i].w;
49                 vis[edges[i].to] = vis[v] + 1;
50                 if(vis[edges[i].to] > n){
51                     cout << "Has negative ring!";
52                     return; 
53                 }
54                 if(!inq[edges[i].to]){
55                     que.push(edges[i].to);
56                     inq[edges[i].to] = true;
57                 }
58             }
59         }
60     }
61     cout << dis[n];
62 }
63 int main()
64 {
65     cin >> n >> m;
66     init();
67     for(int i = 1;i <= m;i++){
68         int u,v,w;
69         cin >> u >> v >> w;
70         add(u,v,w);
71     }
72     spfa(1);
73     return 0;
74 }

三、题目试炼

　　1.P2136 拉近距离 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

　　2.P3385 【模板】负环 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

posted @ 2022-02-16 20:39  scannerkk  阅读(115)  评论(0)    收藏  举报