Dijkstra和Floyd

一、最短路径算法

　　1.Dijkstra（迪杰特斯拉）也叫作单源最短路径算法

　　2.Floyd（弗洛伊德）是个多源最短路径算法

二、Dijkstra算法（采用贪心思想）

　　1.产生

　　　　当我们要计算两个确定的点之间的最小成本的时候，我们就能用到这个算法，比如说我们要从长沙去到北京，可以直达，也可以转车，但是你现在手头有点紧，所以你需要挑选最便宜的价格。你一打开百度地图，发现这么多的路线，人都麻了，所以你现在需要人工找一条便宜的路线，当路线太多的时候我们显然不能够很有效的处理这个问题，因此我们需要计算机来实现这个功能，这个神犇的算法完美的解决了这个复杂的问题。

　　2.基本思想

　　　　利用已知的最短路径，对未知的最短路径进行松弛操作，所以松弛，就是使这两个点的距离变少

　　　　　　比如说

　　　　　　　　

 

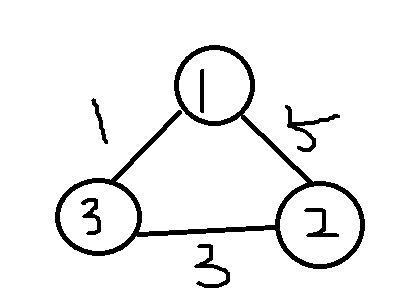
 　　　　此时1-2的距离为5，但我们通过到3，再到2，会把1-2的路径松弛，也就是变短。

　　　　也就是说我们每次从已知的距离中挑选一个最小的，然后从这个点开始对其他的边进行松弛操作，这样操作n-1次，就能够把这个最短路径找出来

　　　　重点来啦

　　　　　　Dijkstra算法不能判断负环的出现，因为是基于贪心的思想。我们来看张图。彻底理解Dijkstra

　　　　

 

 

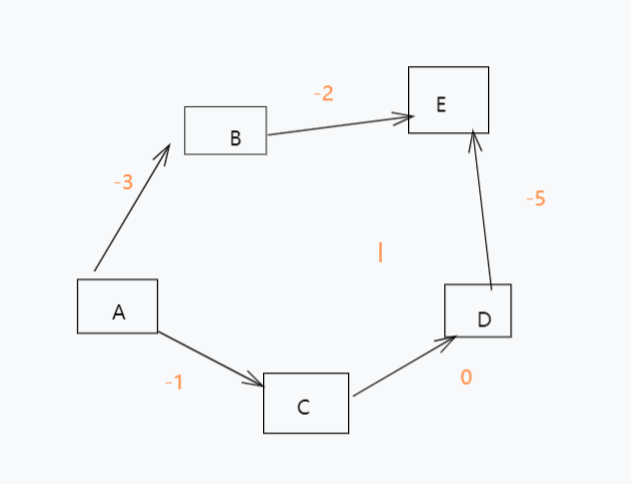
 　　　　会导致E提前更新了，但其实不是最短的。

　　代码实现　　　　

 1 #include "bits/stdc++.h"
 2 #define inf 999999999
 3 using namespace std;
 4 int graph[110][110];
 5 int dis[110];//表示距离
 6 int pre[110];//标记这个顶点的前驱，打印路径
 7 int vis[110];//标记是否为最短路径点
 8 int n,m;//n代表顶点数，m代表边数
 9 void printRoad(int u)
10 {
11     if(u == -1)
12         return;
13     printRoad(pre[u]);
14     if(u != n)
15         cout << u << "-->";
16     else 
17         cout << u;
18 }
19 int main()
20 {
21     cin >> n >> m;
22     for(int i = 1;i <= n;i++)//初始化距离
23         dis[i] = inf;
24     for(int i = 1;i <= n;i++)//初始化前驱
25         pre[i] = -1;
26     for(int i = 1;i <= n;i++)//初始化图表
27         for(int j = 1;j <= n;j++)
28             if(i == j)
29                 graph[i][j] = 0;
30             else    
31                 graph[i][j] = inf;
32     for(int i = 1;i <= m;i++) {
33         int sx,sy,sw;
34         cin >> sx >> sy >> sw;
35         graph[sx][sy] = sw;
36         graph[sy][sx] = sw;
37     }
38     for(int i = 2;i <= n;i++){//初始化1-i距离
39         dis[i] = graph[1][i];
40         pre[i] = 1;//i号节点的前驱为1
41     }
42     vis[1] = 1;//标记1号顶点已经确定为最短路径点
43     for(int i = 2;i <= n;i++){
44         int m = inf;
45         int k;
46         for(int i = 2;i <= n;i++) {
47             if(!vis[i] && dis[i] < m){//寻找已知距离最短的路径，然后再进行新的路径寻找
48                 m = dis[i];
49                 k = i;
50             }
51         }
52         vis[k] = 1;//标记k已经为最短路
53         for(int i = 2;i <= n;i++) {
54             if(!vis[i] && graph[k][i] + m < dis[i]) {//利用k点进行松弛操作
55                 dis[i] = graph[k][i] + m;
56                 pre[i] = k;//更新i的前缀为k
57             }
58         }
59     }
60     printRoad(9);
61     return 0;
62 }

 

堆优化版本1 利用pair的自序实现

 1 #include "bits/stdc++.h"
 2 using namespace std;
 3 #define PII pair<int,int>
 4 int heads[1001000];
 5 int dis[1001000];
 6 bool vis[1001000];
 7 const int inf = 1e9 + 20;
 8 int n,s,d;
 9 int cnt;
10 struct node{
11     int u;
12     int v;
13     int w;
14     int nxt;
15 }edge[10000010];
16 void add(int u,int v,int w)
17 {
18     edge[++cnt].u = u;
19     edge[cnt].v = v;
20     edge[cnt].w = w;
21     edge[cnt].nxt = heads[u];
22     heads[u] = cnt;
23 };
24 void dji()
25 {
26     dis[s] = 0;
27     priority_queue <PII,vector<PII>,greater<PII> > que;
28     que.push({0,s});
29     while(!que.empty()){
30         pair v = que.top();
31         que.pop();
32         if(vis[v.second]) continue;
33         vis[v.second] = true;
34 //         cout << v.second << endl;
35         for(int h = heads[v.second];h != -1;h = edge[h].nxt){
36             if(dis[edge[h].v] > dis[edge[h].u] + edge[h].w){
37                 que.push({dis[edge[h].v],edge[h].v});
38                 dis[edge[h].v] = dis[edge[h].u] + edge[h].w;
39             }
40         }
41     }
42 }
43 int main()
44 {
45     ios::sync_with_stdio(false);
46     cin >> n >> s >> d;
47     for(int i = 0;i <= d;i++)
48         dis[i] = inf,heads[i] = -1;
49     for(int i = 1;i <= n;i++){
50         int u,v,w;
51         cin >> u >> v >> w;
52         add(u,v,w);
53     }  
54     dji();
55     if(dis[d] != inf)
56         cout << dis[d];
57     else
58         cout << -1;
59     return 0;
60 }

 

堆优化版本2利用重构函数实现排序

 1 #include "bits/stdc++.h"
 2 using namespace std;
 3 #define PII pair<int,int>
 4 int heads[1001000];
 5 int dis[1001000];
 6 bool vis[1001000];
 7 const int inf = 1e9 + 20;
 8 int n,s,d;
 9 int cnt;
10 struct node{
11     int u;
12     int to;
13     int w;
14     int nxt;
15     bool operator < (const node &other) const {
16         return w > other.w;
17     }
18 }edge[10000010];
19 void add(int u,int v,int w)
20 {
21     edge[++cnt].u = u;
22     edge[cnt].to = v;
23     edge[cnt].w = w;
24     edge[cnt].nxt = heads[u];
25     heads[u] = cnt;
26 };
27 void dji()
28 {
29     dis[s] = 0;
30     priority_queue <node> que;
31     que.push({0,s,0,-1});
32     while(!que.empty()){
33         node v = que.top();
34         que.pop();
35         if(vis[v.to]) continue;
36         vis[v.to] = true;
37         for(int h = heads[v.to];h != -1;h = edge[h].nxt){
38             if(dis[edge[h].to] > dis[edge[h].u] + edge[h].w){
39                 que.push({0,edge[h].to,dis[edge[h].to],-1});
40                 dis[edge[h].to] = dis[edge[h].u] + edge[h].w;
41             }
42         }
43     }
44 }
45 int main()
46 {
47     ios::sync_with_stdio(false);
48     cin >> n >> s >> d;
49     for(int i = 0;i <= d;i++)
50         dis[i] = inf,heads[i] = -1;
51     for(int i = 1;i <= n;i++){
52         int u,v,w;
53         cin >> u >> v >> w;
54         add(u,v,w);
55     }  
56     dji();
57     if(dis[d] != inf)
58         cout << dis[d];
59     else
60         cout << -1;
61     return 0;
62 }

三.Floyd算法（采用动态规划思想）

　　1.产生

　　　　当我们需要求很多个点之间的最短路径时，我们需要执行很多次Dijkstra算法，代码量还是比较大的，但是这位神犇发明了一个只有五行就解决多个点之间的最短路径问题。

　　2.基本思想

　　　　我们把原先的距离利用松弛操作，不断的借助中间点进行路径松弛，这样就能够把某两个点的路径全部松弛完毕了。如上图，我们求1-2的距离，我们借助3松弛了1-2的距离。我们把每一段距离都枚举出每一个中转点，既可以求得这段距离的最短路径。

　　代码实现

 1 #include "bits/stdc++.h"
 2 #define inf 999999999
 3 using namespace std;
 4 int dis[110][110];//i , j 代表从i到j的权值和
 5 int pre[110][110];//i , j 代表从i到j的路径
 6 void printRoad(int sx,int sy)//打印路径
 7 {
 8     cout << "path:" << endl;
 9     cout << sx;
10     int k = pre[sx][sy];//获取前驱节点
11     while(k != sy){
12         cout << "-->" << k;
13         k = pre[k][sy];
14     }
15     cout << "-->" << sy << endl;
16 }
17 int main()
18 {
19     int n,m;
20     cin >> n >> m;
21     for(int i = 1;i <= n;i++)//初始化距离
22         for(int j = 1;j <= n;j++)
23             if(i == j)
24                 dis[i][j] = 0;
25             else 
26                 dis[i][j] = inf;
27     for(int i = 1;i <= m;i++){
28         int sx,sy,sw;
29         cin >> sx >> sy >> sw;
30         dis[sx][sy] = sw;
31         dis[sy][sx] = sw; 
32     } 
33     for(int i = 1;i <= n;i++)//初始化前驱
34         for(int j = 1;j <= n;j++)
35             pre[i][j] = j;
36     for(int k = 1;k <= n;k++)//借助k点进行中转（松弛）
37         for(int i = 1;i <= n;i++)
38             for(int j = 1;j <= n;j++)
39                 if(dis[i][k] + dis[k][j] < dis[i][j]){
40                     dis[i][j] = dis[i][k] + dis[k][j];
41                     pre[i][j] = pre[i][k];//标记前驱为pre[i][k] 经过p[i][k]中转而来
42                 }
43     cout << "Please input start vertex and end vertex" << endl;
44     int sx,sy;
45     cin >> sx >> sy;
46     printRoad(sx,sy);
47     return 0;
48 }

四.总结

　　今天复习了一下这两个有环图的算法，对这两个算法的理解程度又进了一步！　

posted @ 2022-02-01 21:41  scannerkk  阅读(138)  评论(0)    收藏  举报