BST、TBT构建
一、前言
BST及(BinarySearchTree)二叉查找树,TBT及(ThreadedBinaryTree)线索二叉树。二叉查找树在一定程度上能使查找某个数字从线性变成对数级的时间复杂度,但一定程度上也会失效。线索二叉树是利用空余的指针为二叉树建立一个线性阶的查找,能很快的知道某个节点的前驱和后继。什么是前驱和后继?(比如说ABCD)B的前驱是A,后继是C
二、BST
构建的方法非常简单
1.当前节点为空节点的话就创建一个节点,把要插入的数值放进去即可
2.插入节点的值,大于根节点,则往根节点的右边插入
3.插入节点的值,小于根节点,则往根节点的左边插入
比如说我要插入7,5,9,8,
首先树为空直接申请节点,把7放入节点即可
插入5,5<7,则把5放在7的左边
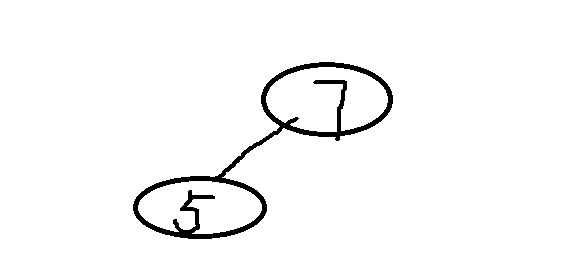
插入9,9>7,放在7的右边
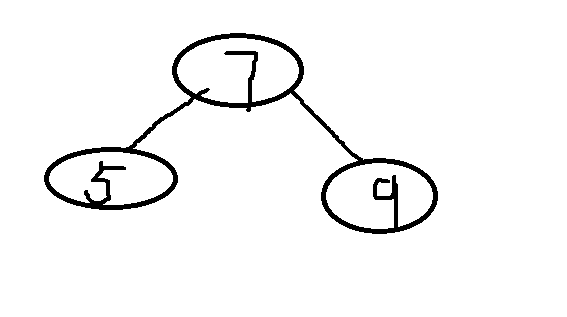
插入8,8>7在7的右边,发现右边有9了,继续判断8<9,9左边为空,则放在9的左边
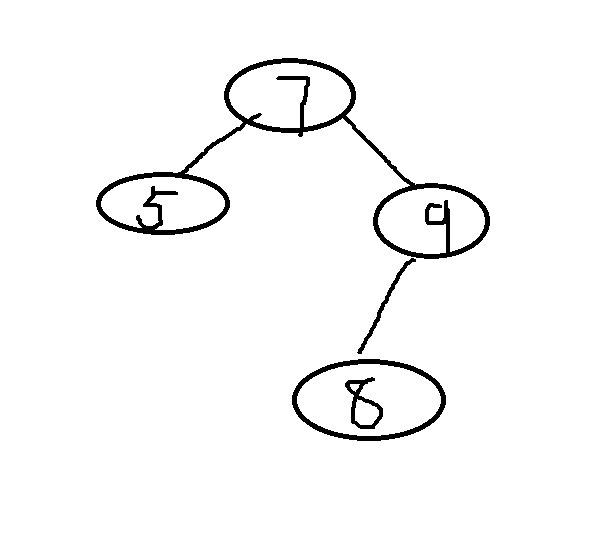
代码实现:
1 #include "bits/stdc++.h" 2 using namespace std; 3 struct node{ 4 int num; 5 node *left = NULL; 6 node *right = NULL; 7 }; 8 node* createBST(int val,node *root)//构建BST 9 { 10 if(root == NULL){ 11 root = new node(); 12 root->num = val; 13 } 14 else { 15 if(root->num == val)//如果存在则不插入 16 cout << "Exist!\n"; 17 else if(val > root->num)//比根大的话往右边插入 18 root->right = createBST(val,root->right); 19 else 20 root->left = createBST(val,root->left);//比根小的话往左边插入 21 } 22 return root; 23 } 24 void bfs(node *root)//层次遍历确定bst创建正确性 25 { 26 queue <node*> q; 27 q.push(root); 28 while(!q.empty()){ 29 int len = q.size(); 30 for(int i = 0;i < len;i++){ 31 node *v = q.front(); 32 cout << v->num << " "; 33 q.pop(); 34 if(v->left) q.push(v->left);//左子树存在 35 if(v->right) q.push(v->right);//右子树存在 36 } 37 } 38 cout << endl; 39 } 40 void find(int val,int cnt,node *root) 41 { 42 if(root == NULL) 43 cout << val << " Unexist\n"; 44 else { 45 if(root->num == val) 46 cout << "Find it " << cnt + 1<< endl; 47 else if(root->num < val)//比查找的数小的话往右边走 48 find(val,cnt+1,root->right); 49 else //比查找的数打的话往左边走 50 find(val,cnt+1,root->left); 51 } 52 } 53 void del(int val,node *root) 54 { 55 if(root == NULL) 56 cout << "Unexist" << endl; 57 else { 58 node *q = root; 59 node *qfather = root; 60 while(q != NULL && q->num != val){ 61 qfather = q; 62 if(val > q->num) 63 q = q->right; 64 else 65 q = q->left; 66 } 67 if(!q) 68 cout << "Unexist\n"; 69 else { 70 if(q->left == NULL && q->right == NULL) {//左子树和右子树都为空 71 if(qfather->left == q)//如果删除的是左子树,那么父亲节点的左子树为空 72 qfather->left = NULL; 73 else 74 qfather->right = NULL;//如果删除的是右子树,那么父亲节点的右子树为空 75 delete(q); 76 } 77 else if((q->left != NULL && q->right == NULL) || (q->left == NULL && q->right != NULL)) {//左子树或者右子树为空 78 if(q->left){//如果删除节点有左子树 79 if(qfather->left == q) 80 qfather->left = q->left; 81 else 82 qfather->right = q->left; 83 } 84 else {//如果删除节点有右子树 85 if(qfather->left == q) 86 qfather->left = q->right; 87 else 88 qfather->right = q->right; 89 } 90 delete(q); 91 } 92 else {//左子树和右子树都不为空 93 node *qright = q->left; 94 node *qrightfather = q; 95 cout << qright->num << endl; 96 while(qright->right != NULL) {//往删除节点的左子树的右子树走到尽头 97 qrightfather = qright;//记录他的父亲节点 98 qright = qright->right; 99 } 100 q->num = qright->num;//把右子树的尽头的值赋给删除节点 101 if(qright == q->left)//如果当前节点的左子树没有右子树,则直接把当前节点的左子树移上去,那么删除节点的左子树则为空了 102 q->left = NULL; 103 else if(qright->left != NULL) //如果最右边的节点有左子树,那么就需要用他父亲的右子树接上他的左子树 104 qrightfather->right = qright->left; 105 delete(qright);//释放最右边的节点 106 } 107 } 108 } 109 } 110 int main() 111 { 112 node *root = NULL; 113 root = createBST(9,root); 114 root = createBST(5,root); 115 root = createBST(11,root); 116 root = createBST(3,root); 117 root = createBST(7,root); 118 root = createBST(6,root); 119 root = createBST(3,root); 120 root = createBST(10,root); 121 root = createBST(12,root); 122 bfs(root);//按层次打印节点 123 // del(8,root); 124 // del(6,root); 125 // del(9,root); 126 del(5,root); 127 bfs(root); 128 return 0; 129 }
三、TBT
1线索二叉树的背景.
首先我们了解一下这棵树产生的背景,当我们有n的节点时,我们的左右指针的个数将会达到2n个,而实际我们需要用到的仅仅只有n-1个,那么我们剩下的n+1个指针不是浪费了吗?那我们怎样利用他们呢?我们分析当我们中序遍历某树为CBEGDFA,那我们如果要找某个节点的前一个,和某个节点的后一个,怎么找呢?重新遍历一边?每次找都要遍历一遍?这样既浪费时间,也浪费空间了。因此就有了线索二叉树。通过空余的指针指向前驱或者后继,十分聪明的想法,那么如果原来的指针已经被用来指向孩子了呢,我现在再移动这个指针是不是会把树结构打乱?于是乎我们就产生了lflag和rflag两个布尔型变量。用来记录每个节点是否有了孩子节点。lflag就是是否有了左孩子节点,rflag就是是否有了右孩子节点。
2思路分析
介绍完线索二叉树的背景后,我们来分析一下这个树该怎么构建呢?
首先我们根据平时构树的习惯,根据前序构建一棵树。
然后利用中序遍历,把这棵树改造一下,就可以变成一棵TBT树了。
跟中序遍历一样,先跑左子树,再回到根,最后跑右子树
我们遍历的时候是打印,这里把打印改成指针的指向操作就行啦!思路十分简单,就是代码细节很多,所以要认真!
首先我先拿出一棵普通的二叉树,然后根据中序一点一点画出线索二叉树
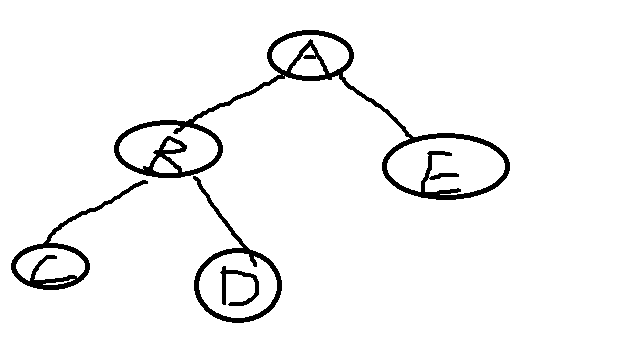
此时我们已经构造完一棵二叉树了,开始中序遍历构造线索二叉树
中序遍历:CBDAE
1.首先,我们根据中序遍历
先走到了C,然后发现C的左孩子为空,但是C又没有前驱,所以我们把他的前驱指向空NULL
然后发现C的右孩子也为空,C的后继为B,但是我们还没有遍历到B呢,所以先存起来,等下一次再处理这个节点的后继
2.我们来到了B,这时候发现B的左孩子不为空,右孩子也不为空,但是我们的前驱节点的后继还没有指向,所以我们先把C的后继指向B
3.我们来到了D,此时发现D的左右孩子都为空,D的前驱为B,所以D的指针指向了B,D的右指针也为空,但是现在没有找到下一个,所以先存起来,等会走到了A的时候再指向即可
4.我们来到了A,此时A的左右孩子都不为空,我们只需要把上一次存的节点的后继指向A即可
5.我们来到了E,发现E的左右孩子都为空,我们把左指针指向A,但是E没有后继了,所以我们把E的后继指向空
6.至此我们的线索二叉树已经构建完毕!
树图为
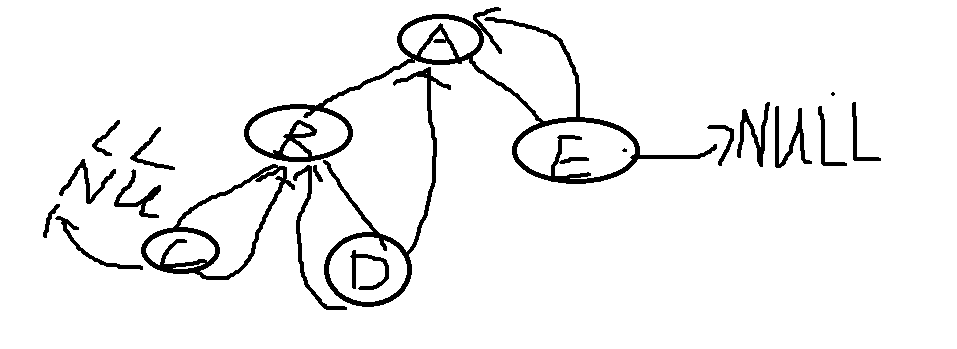
代码实现:
1 #include "bits/stdc++.h" 2 using namespace std; 3 struct node{ 4 char data; 5 node *lchild = NULL; 6 node *rchild = NULL; 7 bool lflag = false; 8 bool rflag = false; 9 }; 10 node *pre;//记录前驱节点 11 node * createTree()//按前序建树 12 { 13 node *T = new node(); 14 char ch; 15 cin >> ch; 16 if(ch == '#') 17 return NULL; 18 T->data = ch; 19 T->lchild = createTree(); 20 T->rchild = createTree(); 21 return T; 22 } 23 void ThreadTBT(node *root)//线索化Tree 24 { 25 if(root == NULL) 26 return; 27 ThreadTBT(root->lchild);//一直跑到左端点 28 if(!root->lchild){ 29 root->lflag = true;//表示可以这个节点的指针可以用来指向前驱节点 30 root->lchild = pre; 31 } 32 if(pre != NULL && !pre->rchild){//利用上一个节点来判断 33 pre->rflag = true;//表示这个节点的指针可以用来指向后驱节点 34 pre->rchild = root; 35 } 36 pre = root; 37 ThreadTBT(root->rchild); 38 } 39 void createTBT(node *root) 40 { 41 pre = NULL; 42 if(root){ 43 ThreadTBT(root);//中序遍历线索化 44 pre->rchild = NULL; 45 pre->rflag = true;//最后一个节点线索化 46 } 47 } 48 void traverseTBT(node *T)//遍历TBT 49 { 50 node *p; 51 p = T; 52 while(p){//因为是中序,所以遍历顺序是左根右 53 while(p->lflag == false)//false表示原指针,true表示后继指针 这里是找到每棵子树的最后一个左孩子 54 p = p->lchild; 55 cout << p->data; 56 while(p->rflag == true && p->rchild){//找到后继节点,就是下一次要输出的那个节点的根 57 p = p->rchild; 58 cout << p->data; 59 } 60 p = p->rchild;//继续从右子树开始按同样的方式遍历右子树 61 } 62 } 63 int main() 64 { 65 node *root = createTree();//(test1:ABC##DE#G##F### answer1:CBEGDFA test2:ABDH##I##EJ###CF##G## answer2:HDIBJEAFCG) 66 createTBT(root); 67 traverseTBT(root); 68 return 0; 69 }
四、总结
跟着《大话数据结构》写个线索二叉树写了好多bug,总之又臭又长,然后自己debug一天,把代码缩到了七十行(原来有一百三十行),收获挺大的,对于树结构的了解程度又进步了!
本文来自博客园,作者:{scanner},转载请注明原文链接:{https://home.cnblogs.com/u/scannerkk/}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号