递归求解Ackermann函数和n皇后回溯问题

一.前言：

人傻钱不多，只求期末不挂科！

二.递归的基础

(1)递归的概念：所谓递归就是一个函数自己调用自己，然后不断向下走，直到出口，也就是得出了解

(2)递归的要素：

　　1.递归的参数（就是要求解某一个东西，需要用到的变量）

　　2.结束条件（也就是递归的出口）

　　3.递归的方向（像迷宫类的程序就是多个方向递归）

三.递归习题

1.Ackermann函数求解

　　阿克曼函数原型为

　　

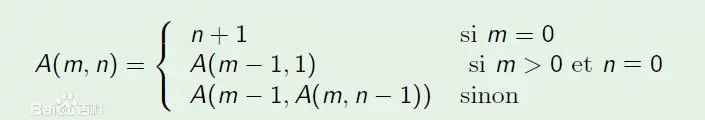
因此我们可以写出如下程序：

#include "bits/stdc++.h"
using namespace std;
//Ackermann函数原型（增长特别快）
//Ackermann反函数则下降特别快
int ack(int m,int n)//递归做法
{
    if(m == 0)  return n + 1;
    else if(n == 0) return ack(m - 1,1);
    else  return ack(m-1,ack(m,n-1));
}
int main()
{
    cout << ack(1,2);
    return 0;
}

这个函数的原型是简单的，看起来运算是小的，但是如果运行一个4，3就会算不过来，这个深度非常深，所以这个函数增长特别快，所以它的反函数增长特别慢。

 

2.n皇后回溯问题

前段时间刷oj时碰到了一个求解n皇后解法，但并没有让我实现解法的打印，于是乎我就做了一个解法打印，中途有点小bug，不过还是解决了>0<。现在将代码贴出，里面写有注释。

#include "bits/stdc++.h"
using namespace std;
int attack[11][11];
int n;//代表n皇后
int cnt;//代表有多少种解法
char queen[11][11];//初始化棋盘
const int mv[8][2] ={{-1,0},{1,0},{0,-1},{0,1},{-1,-1},{1,1},{1,-1},{-1,1}};//八个方向
void init(int n)//初始化棋盘数组
{
    for(int i = 1;i <= n;i++)
        for(int j = 1;j <= n;j++)
            queen[i][j] = '.';
}
void mark(int x,int y,int flag)//flag = 0代表取消标记，flag = 1,代表标记
{
    for(int i = 1;i <= n * sqrt(2) + 1;i++)//表示最大可以遍历多少个点,n*sqrt(2)+1是计算最大可以攻击的范围，因为在矩阵中对角线一定最长
        for(int j = 0;j <= 7;j++){
            int dx = x + i * mv[j][0];
            int dy = y + i * mv[j][1];
            if(dx < 0 || dx > n || dy < 0 || dy > n)
                continue;
            if(!attack[dx][dy] && flag)//如果还没有做过标记
                attack[dx][dy] = x;
            else if(attack[dx][dy] == x && !flag)//取消标记
                attack[dx][dy] = 0;
        }
}
void solve(int f)//f代表处理到第几行了
{
    if(f == n+1){
        cnt++;
        cout << cnt << "th:" << endl;
        for(int i = 1;i <= n;i++){//打印解法
            for(int j = 1;j <= n;j++)
                cout << queen[i][j];
            cout << endl;
        }
        cout << endl;cout << endl;
        return;
    }
    for(int j = 1;j <= n;j++){
        if(!attack[f][j]){//f代表第多少行的皇后
            attack[f][j] = f;//标记皇后这个点
            queen[f][j] = 'Q';//标记这个皇后
            mark(f,j,1);//给攻击范围做上标记
            solve(f+1);
            attack[f][j] = 0;//取消标记，回溯
            queen[f][j] = '.';//把这个皇后取消
            mark(f,j,0);//取消该皇后的攻击标记
        }
    }
}
int main()
{
    cin >> n;
    init(n+1);//初始化棋盘数组
    solve(1);//开始求解
    cout << cnt << endl;//打印一共有多少种解法
    return 0;
}

 

四.总结

临近期末没什么时间做更多的题，只好把以前未实现的想法现在想到了就实现一下，最后期末一定不要挂AAAAAAA!