参考内容：书籍《卡尔曼滤波原理及应用------matlab仿真》这本书对kalman算法的解析很清晰，MATLAB程序很全，适合初学者（如有侵权，请联系删除(qq:1491967912)）
1、三维寻地制导系统
在三维平面x-y-z内运动的质点M，其在某一时刻k的位置、速度和加速度可用公式1矢量表示。
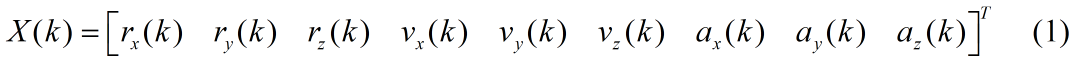
其中r(k)、v(k)、a(k)分别表示距离、速度和加速度。质点M在三维空间内做任何运动，在x,y,z三个方向上还应考虑加性系统噪声W（k），所以在笛卡尔坐标系下该质点的状态方程可以表示为：
通常情况下EKF的状态方程式是线性的，可表示为公式3的形式：
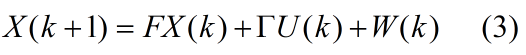
式中：
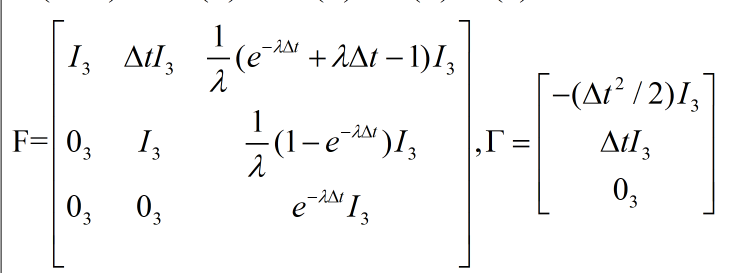
U是三个方向上的导弹加速度。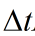
为测量周期，也可以称其为扫描周期、采样时间间隔。动态噪声W(k)为：
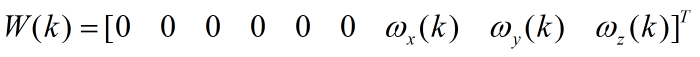
并且该噪声的均值和协方差可表示为：
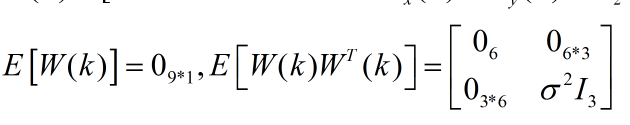
从上述结果可以看出W（k）是高斯白色随机向量序列。
考虑一个带有观测器的飞行中得导弹，假设其为质点M，对移动的目标进行观测，导弹和目标的相对位置依然可用x,y,z表示。
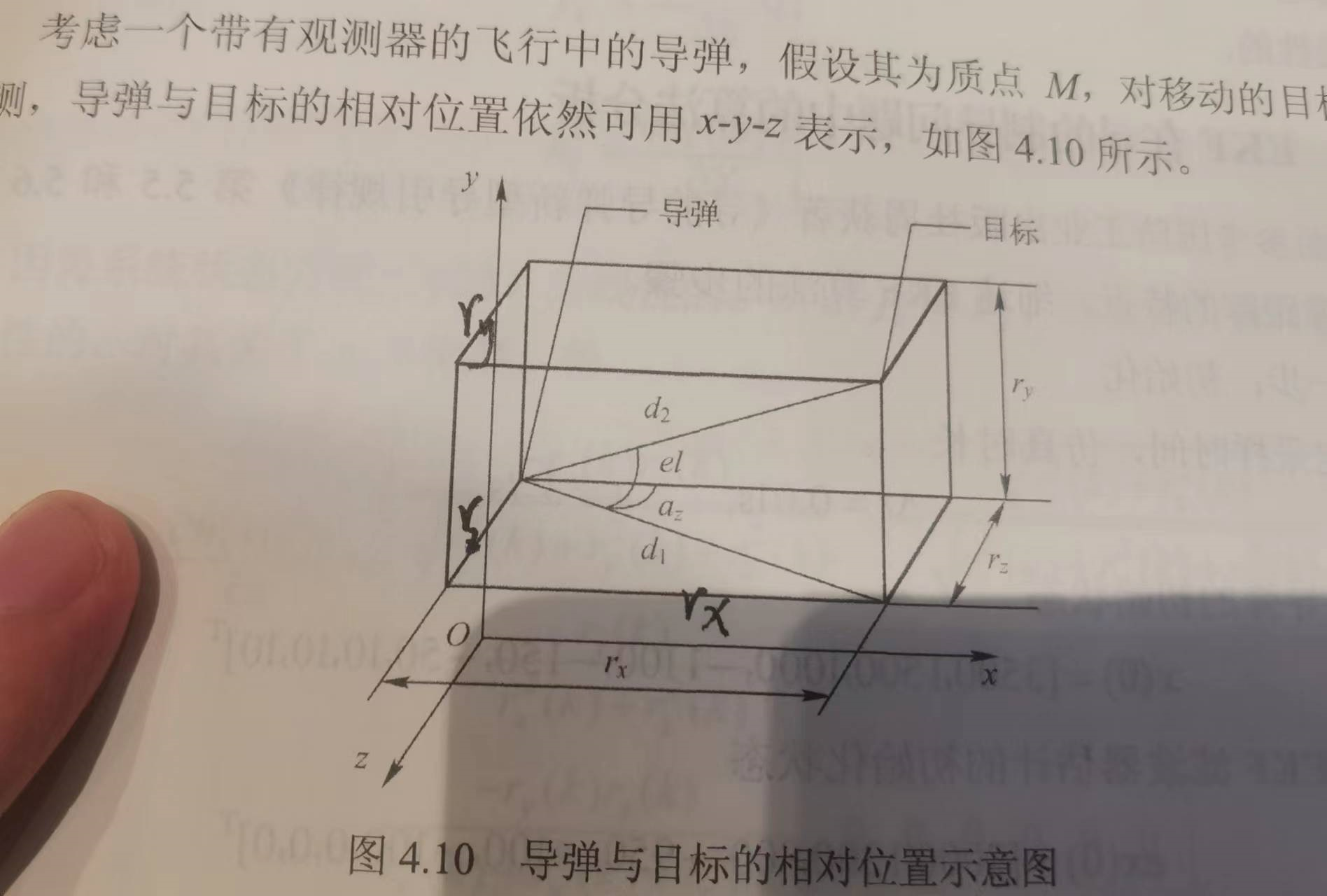
导弹对目标采用纯方位观测，观测量为俯仰角（图中的el）和水平方向偏向角（图中的a2），实际测量中雷达具有加性测量噪声V（k）,在笛卡尔坐标系下，观测方程为：
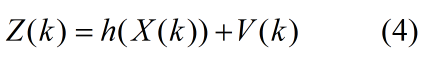
式中：
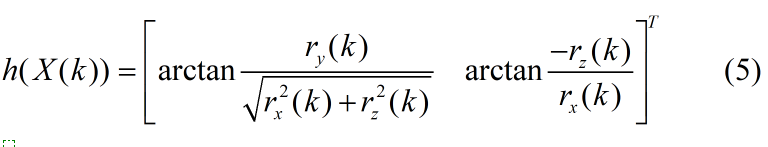
V(k)为测量噪声，是高斯白色随机向量序列，
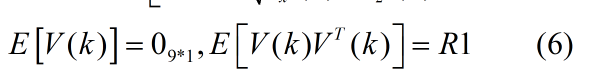
其中R1定义为：
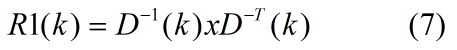其中
，
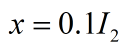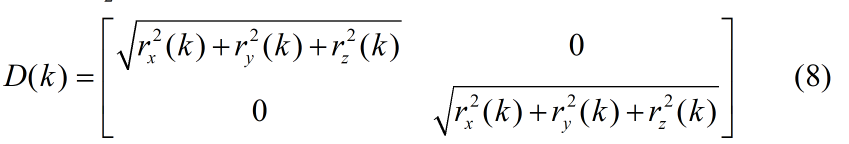
根据4~8的公式可知，在笛卡尔坐标系下，该运动模型的观测方程是非线性的。
2、EKF在寻地制导问题中的算法分析
第一步：初始化
设定采样时间，仿真时长
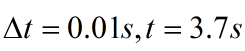
设定导弹的初始状态。
x(0)=[3500,1500,1000,-1100,-150,-50,0,0,0]T,
设定EKF滤波器估计的初始化状态:
ex(0)=[3000,1200,960,-800,-100,-100,0,0,0]T
设定过程噪声方差：
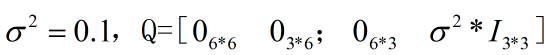
初始化EKF滤波器估计的状态协方差矩阵：
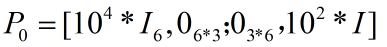
第二步：EKF滤波估计：
for k=1:T
step1:目标运动
x(:,k)=F*x(:,k-1)+G*u(:,k-1)+w(:,k-1);
step2:每次间隔Δt=0.01s对目标扫描，即观测。
Z(:,k)=[atan(X(2,k)/sqrt(X(1,k)^2+X(3,k)^2)),atan(-X(3,k)/X(1,k))]'+v(:,k);
step3：计算统计方差估计R，R=0.1*eye(2)/(DD*DD');
step4：状态预测（结合kalman滤波核心算法），Xn=F*ex+G*u;
step5：观测预测，（参见程序）
step6：协方差阵预测：P=F*P0*F'+Q;
step7：这一步是EKF独有的，也是EKF的核心部分，计算线性H矩阵，对于本文来说的非线性系统公式2和公式5来说。定义为：
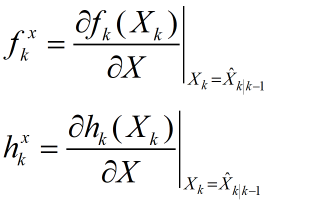
因为系统的状态方程是线性的，所以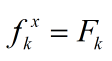
，而观测方程是非线性的，对其关于X(k)求导（另外给出几个求偏导要用到的公式）：
首先是链式法则：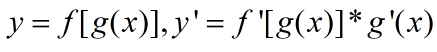
其次：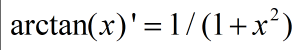
另外：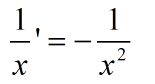
基本上根据上面三个公式就能求观测方程的偏导：
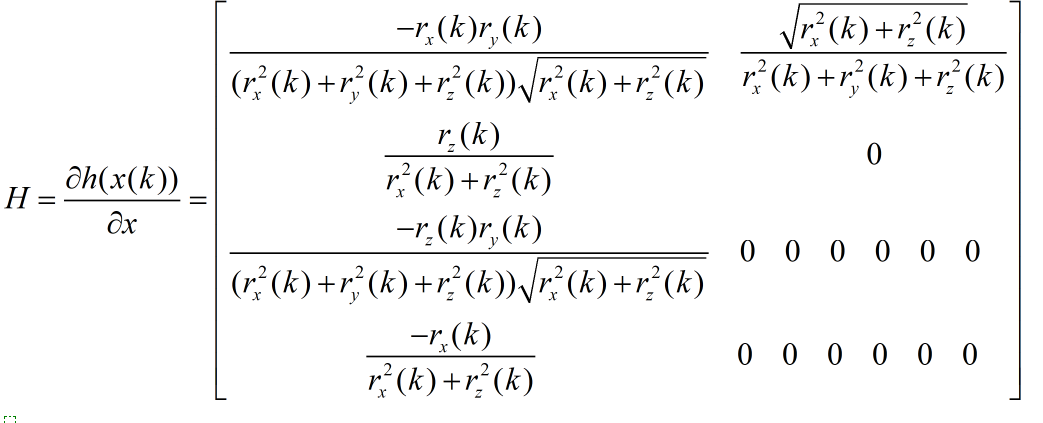
step8：计算kalman滤波器增益K=P*H'/(H*P*H'+R);
step9:状态更新ex=Xn+K*(z-Zn)
step10:协方差阵更新：P0=(I-K*H)*P；
END
3、仿真结果
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%程序说明：目标跟踪程序，实现运动弹头对运动物体的三维跟踪
%%%%状态方程：x(t)=Ax(t-1)+Bu(t-1)+w(t)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
clc
clear all
close all
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
t=0.01; %采样时间
T=4; %仿真时长
gama=10000; %机动频率
N=T/t; %采样点数
%状态转移矩阵，F表示
I=eye(9);
F=[eye(3),t*eye(3),(exp(-1*gama*t)+gama*t-1)*eye(3)/gama^2;zeros(3),eye(3),(1-exp(-gama*t))*eye(3)/gama;zeros(3),zeros(3),exp(-gama*t)*eye(3)];
%控制量驱动矩阵
G=[-(t^2/2)*eye(3);-t*eye(3);zeros(3)];
N1=3; %导航比（制导律）
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
for i=1:50
X=zeros(9,N);
X(:,1)=[3500,1500,1000,-1100,-150,-50,0,0,0]'; %初始状态位置，速度，加速度
X_ekf=zeros(9,N);
X_ekf(:,1)=[3000,1200,960,-800,-100,-100,0,0,0]';
% X_ekf(:,1)=X(:,1); %滤波器状态初始化
cigema=sqrt(0.1);
w=[zeros(6,N);cigema*randn(3,N)]; %过程噪声
Q=[zeros(6),zeros(6,3);zeros(3,6),cigema^2*eye(3)]; %协方差矩阵
Z=zeros(2,N); %观测值
Z(:,1)=[atan(X(2,1)/sqrt(X(1,1)^2+X(3,1)^2)),atan(-X(3,1)/X(1,1))]'; %观测值初始化
% Z(:,1)=[atan(X(2,1)/sqrt(X(1,1)^2+X(3,1)^2)),atan(X(3,1)/X(1,1))]'; %观测值初始化
v=zeros(2,N); %观测噪声
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
for k=2:N-3
tgo=T-k*0.01;
c1=N1/tgo^2; %x方向制导律系数
c2=N1/tgo; %y方向制导律系数
c3=N1/(exp(-gama*tgo)+gama*tgo-1)/(gama*tgo)^2; %z方向制导律系数
%X Y Z三个方向上的导弹加速度
u(1,k-1)=[c1 c2 c3]*[X(1,k-1) X(4,k-1) X(7,k-1)]';
u(2,k-1)=[c1 c2 c3]*[X(2,k-1) X(5,k-1) X(8,k-1)]';
u(3,k-1)=[c1 c2 c3]*[X(3,k-1) X(6,k-1) X(9,k-1)]';
%目标状态方程
X(:,k)=F*X(:,k-1)+G*u(:,k-1)+w(:,k-1);
d=sqrt(X(1,k)^2+X(2,k)^2+X(3,k)^2); %计算距离
D=[d,0;0,d];
%计算观测噪声协方差矩阵
R=inv(D)*0.1*eye(2)*inv(D)'; %观测噪声方差
v(:,k)=sqrt(R)*randn(2,1); %观测噪声
%目标观测方程
Z(:,k)=[atan(X(2,k)/sqrt(X(1,k)^2+X(3,k)^2)),atan(-X(3,k)/X(1,k))]'+v(:,k);
% Z(:,k)=[atan(X(2,k)/sqrt(X(1,k)^2+X(3,k)^2)),atan(X(3,k)/X(1,k))]'+v(:,k);
end
%下面根据观测值开始滤波
P0=[10^4*eye(6),zeros(6,3);zeros(3,6),10^2*eye(3)]; %协方差初始化
step=0.5/0.01;
span=1/0.01;
for k=2:N-3
dd_ekf=sqrt(X_ekf(1,k-1)^2+X_ekf(2,k-1)^2+X_ekf(3,k-1)^2);
DD_ekf=[dd_ekf,0;0,dd_ekf];
RR=0.1*eye(2)/(DD_ekf*DD_ekf');
% RR=inv(DD_ekf)*0.1*eye(2)*inv(DD_ekf)';
tgo=T-k*0.01;
c1=N1/tgo^2; %x方向制导律系数
c2=N1/tgo; %y方向制导律系数
c3=N1/(exp(-gama*tgo)+gama*tgo-1)/(gama*tgo)^2; %z方向制导律系数
u1(1,k-1)=[c1 c2 c3]*[X_ekf(1,k-1) X_ekf(4,k-1) X_ekf(7,k-1)]';
u1(2,k-1)=[c1 c2 c3]*[X_ekf(2,k-1) X_ekf(5,k-1) X_ekf(8,k-1)]';
u1(3,k-1)=[c1 c2 c3]*[X_ekf(3,k-1) X_ekf(6,k-1) X_ekf(9,k-1)]';
Xn=F*X_ekf(:,k-1)+G*u1(:,k-1); %状态预测
Zn=[atan(Xn(2)/sqrt(Xn(1)^2+Xn(3)^2)),atan(-Xn(3)/Xn(1))]';
% Zn=[atan(Xn(2)/sqrt(Xn(1)^2+Xn(3)^2)),atan(Xn(3)/Xn(1))]';
P=F*P0*F'+Q; %预测误差协方差
%求观测矩阵H
H=[-Xn(2)*Xn(1)/(Xn(1)^2+Xn(2)^2+Xn(3)^2)/sqrt(Xn(1)^2+Xn(3)^2) sqrt(Xn(1)^2+Xn(3)^2)/(Xn(1)^2+Xn(2)^2+Xn(3)^2) -Xn(2)*Xn(3)/(Xn(1)^2+Xn(2)^2+Xn(3)^2)/sqrt(Xn(1)^2+Xn(3)^2) 0 0 0 0 0 0;...
Xn(3)/(Xn(1)^2+Xn(3)^2) 0 -Xn(1)/(Xn(1)^2+Xn(3)^2) 0 0 0 0 0 0];
K=P*H'/(H*P*H'+R);
X_ekf(:,k)=Xn+K*(Z(:,k)-Zn);
P0=(I-K*H)*P;
end
for t=1:N-3 %求每个时间点误差的平方
Ep_ekf_x(i,t)=sqrt((X_ekf(1,t)-X(1,t))^2);
Ep_ekf_y(i,t)=sqrt((X_ekf(2,t)-X(2,t))^2);
Ep_ekf_z(i,t)=sqrt((X_ekf(3,t)-X(3,t))^2);
Er_ekf(i,t)=sqrt((X_ekf(1,t)-X(1,t))^2+(X_ekf(2,t)-X(2,t))^2+(X_ekf(3,t)-X(3,t))^2);
Ev_ekf(i,t)=sqrt((X_ekf(4,t)-X(4,t))^2+(X_ekf(5,t)-X(5,t))^2+(X_ekf(6,t)-X(6,t))^2);
Ea_ekf(i,t)=sqrt((X_ekf(7,t)-X(7,t))^2+(X_ekf(8,t)-X(8,t))^2+(X_ekf(9,t)-X(9,t))^2);
end
for t=1:N-3
error_x(t)=mean(Ep_ekf_x(:,t));
error_y(t)=mean(Ep_ekf_y(:,t));
error_z(t)=mean(Ep_ekf_z(:,t));
error_r(t)=mean(Er_ekf(:,t));
error_v(t)=mean(Ev_ekf(:,t));
error_a(t)=mean(Ea_ekf(:,t));
end
end
t=0.01:0.01:3.97;
figure
hold on;box on;grid on;
plot3(X(1,:),X(2,:),X(3,:),'-k.');
plot3(X_ekf(1,:),X_ekf(2,:),X_ekf(3,:),'-r.');
legend('真实值','EKF滤波值');
view(3);
xlabel('x/m');
ylabel('y/m');
zlabel('z/m');
title('轨迹图');
figure
hold on;box on;grid on;
plot(t,error_r,'-b.');
xlabel('飞行时间/s');
ylabel('相对位置估计偏差/m');
title('位置偏差图');
figure
hold on;box on;grid on;
plot(t,error_v,'-b.');
xlabel('飞行时间/s');
ylabel('速度估计偏差/m');
title('速度偏差图');
figure
hold on;box on;grid on;
plot(t,error_a,'-b.');
xlabel('飞行时间/s');
ylabel('加速度估计偏差/m');
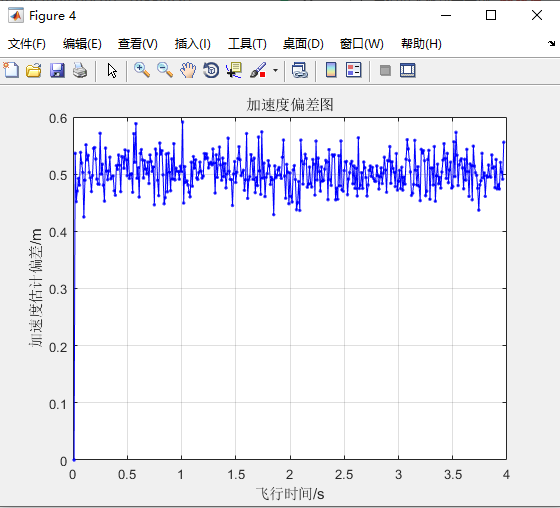
title('加速度偏差图');
%}
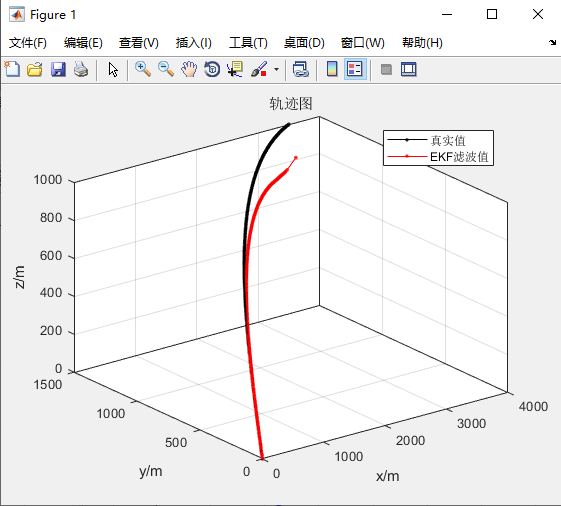
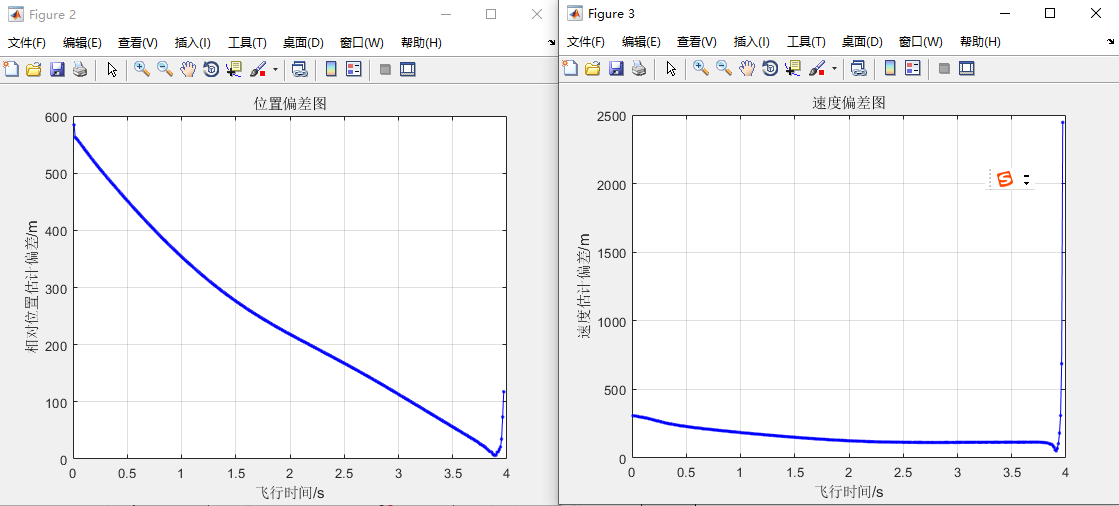
从图1仿真结果来看，跟踪轨迹能够较好的跟踪目标，虽然该开始误差较大，但随着跟踪的进行，轨迹最后基本趋于一致；同样计算EKF滤波后的状态值与目标真实状态之间的偏差，可以得到位置偏差图、速度偏差图和加速度偏差图，如图2~4所示。无论位置还是速度，最终都是收敛的，加速度则最终稳定在特定的值。
另外，本章的EKF以及前面的所有EKF的观测方程都是针对某一个维度（方位、距离、速度）。而针对多个变量的观测方程请参考UKF在匀加速直线运动目标跟踪中的应用以及算法实现里面的观测方程是从两个维度（距离和角度）来论述。后面会出一篇EKF在匀速运动目标跟踪的应用（包含了多个维度的观测方程），敬请期待。
浙公网安备 33010602011771号