今天接着肝卡尔曼滤波，今天针对自由落体运动目标跟踪，由于上一篇针对温度的卡尔曼滤波是一维的测量，较为简单；所以今天的自由落体运动目标的跟踪针对二维来进行。同时还引入了控制矩阵B和控制量U。
首先还是先预习一下卡尔曼的知识。
参考内容：书籍《卡尔曼滤波原理及应用------matlab仿真》
卡尔曼知识
模型建立
观测方程：Z(k)=H*X(k)+V(k）；
状态方程：X(k)=A*X(k-1)+W(k-1);
其中，X（k）为系统在时刻k的状态，Z（k）为对应状态的测量值。W（k）为输入的白噪声（也是过程误差），V（k）为观测噪声（也是测量误差），W（k），V（k）是均值为零，方差阵各为Q和R的不相关白噪声。A为状态转移矩阵，H为观测矩阵。
卡尔曼滤波：
预测 校正
先验估计 ：
卡尔曼增益：
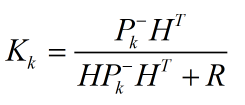
先验协方差误差 ：
后验估计：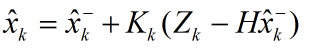
协方差:
样例分析：
某一物体在重力场做自由落体运动，有一观测装置在对物体的位移进行检测，传感器会受到位置的独立分布随机信号的干扰。我们需要估计该物体的运动位移和速度两个变量。
对于上述这个二阶系统，我们已知的是，该物体的加速度为g,设物体的位移x1和速度x2，定义如下的向量
现在推导该自由落体目标的状态转移矩阵。由运动方程，可得到运动物体的状态方程。
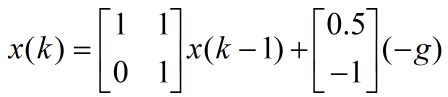
给定位置观测装置，在测量值受到某种独立，随机干扰v(k)的影响时，观测方程可写为：
给定v(k)的方差R（k）=1；物体初始状态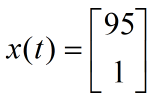
，初始误差为
。
并且由于运动方程的物理模型可知：
(个人理解由于是下落过程中忽略了空气阻力).
在上述条件具备的情况下，可以进行下一步的kalman滤波的递推过程。
其中
另外的递推关系式为：
此外第k+1时刻的预测值可以写为：
按照上述算法流程，对自由落体运动目标进行kalman滤波和预测。
关于自由落体的matlab具体算法如下所示：
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%kalman滤波用于自由落体运动目标的跟踪问题
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
clc
clear all
close all
N=1000; %仿真时间，时间序列号的总数
%噪声
Q=[0 0;0 0]; %过程噪声方差为0，即下落过程中忽略了空气阻力。
R=[1,0;0,1]; %观测噪声方差
W=sqrt(Q)*randn(2,N); %过程噪声
V=sqrt(R)*randn(2,N); %测量噪声
%系统矩阵
A=[1,1;0,1]; %状态转移矩阵
B=[0.5;1]; %控制矩阵
U=1; %控制量，相当于g，此处为了便于计算令其等于1
C=[1,0;0,1]; %观测矩阵，相当于公式中的H
%参数初始化
X=zeros(2,N); %物体真实状态初始化
X(:,1)=[95;1]; %物体真实状态初始位置和速度
P0=[10,0;0,1]; %协方差误差初始化
Z=zeros(2,N); %测量初始化
Z(:,1)=C*X(:,1)+V(:,1); %测量状态初始位置
Xkf=zeros(2,N); %kalman滤波估计状态初始化
Xkf(:,1)=X(:,1); %kalman滤波估计状态初始位置
err_P=zeros(N,2); %误差均方值初始化
err_P(1,1)=P0(1,1);
err_P(1,2)=P0(2,2);
I=eye(2);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
for k=2:N
%物体下落，受状态方程的驱动
X(:,k)=A*X(:,k-1)+B*U+W(:,k);
%测量
Z(:,k)=C*X(:,k)+V(:,k);
%kalman滤波
X_pre=A*Xkf(:,k-1)+B*U;
P_pre=A*P0*A'+Q;
K=P_pre*C'/(C*P_pre*C'+R);
Xkf(:,k)= X_pre+K*(Z(:,k)-C*X_pre);
P0=(I-K*C)*P_pre;
%误差均方差
err_P(k,1)=P0(1,1);
err_P(k,2)=P0(2,2);
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%误差计算
meassure_err_x=zeros(1,N); %测量值与真实值的位移误差
meassure_err_v=zeros(1,N); %测量值与真实值的速度误差
kalman_err_x=zeros(1,N); %kalman估计的位移与真实位移之间的偏差
kalman_err_v=zeros(1,N); %kalman估计的速度与真实速度之间的偏差
for k=1:N
meassure_err_x(k)=Z(1,k)-X(1,k); %测量值与真实值的误差
meassure_err_v(k)=Z(2,k)-X(2,k); %测量值与真实值的速度误差
kalman_err_x(k)=Xkf(1,k)-X(1,k); %kalman估计的位移与真实位移之间的偏差
kalman_err_v(k)=Xkf(2,k)-X(2,k); %kalman估计的速度与真实速度之间的偏差
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%画图输出
%噪声图
figure
plot(W);
xlabel('采样时间/s');
ylabel('过程噪声');
title("过程噪声噪声图");
figure
plot(V);
xlabel('采样时间/s');
ylabel('测量噪声');
title("测量噪声噪声图");
%位置偏差
figure
hold on,box on,grid on;
plot(meassure_err_x,'-r*'); %测量的位移误差
plot(kalman_err_x,'-gs'); %kalman估计位置误差
legend('测量误差','kalman滤波误差');
xlabel('采样时间/s');
ylabel('位置偏差/m');
title("位置的偏差");
figure;
plot(meassure_err_v,'-r*');hold on; %测量的速度误差
plot(kalman_err_v,'-go');
legend('测量误差','kalman滤波误差');
grid on
xlabel('采样时间/s');
ylabel('速度偏差/m');
title("速度的偏差");
%误差均方值
figure
plot(err_P(:,1),'-r');
grid on
xlabel('采样时间/s');
ylabel('位移误差均方值');
title("位移误差均方值");
figure
plot(err_P(:,2),'-b');
grid on;
xlabel('采样时间/s');
ylabel('速度误差均方值');
title("速度误差均方值");
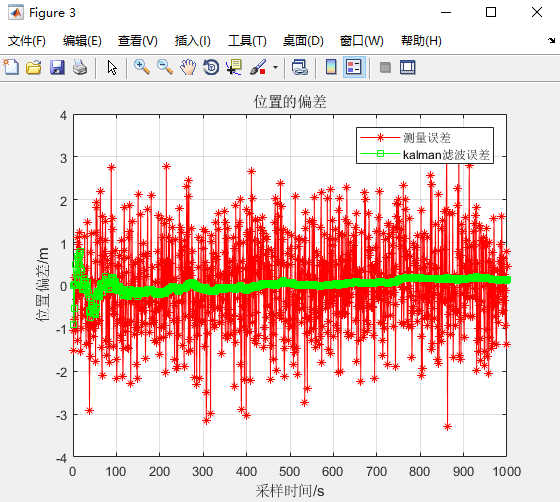
从位置和速度的估计来看，测量值受到测量噪声的影响，但kalman滤波算法则可以很好的降低噪声的干扰，在经过少数迭代后误差很快的收敛。
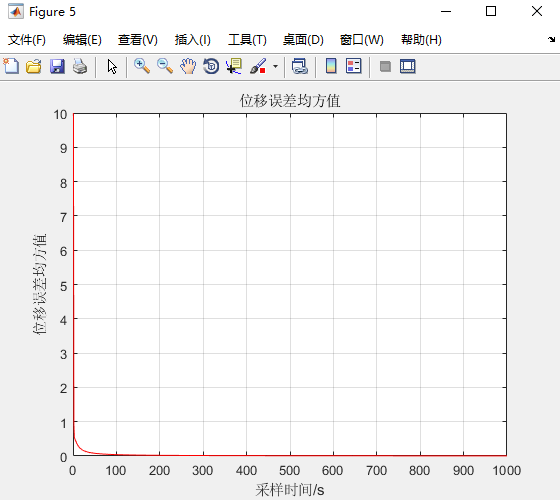
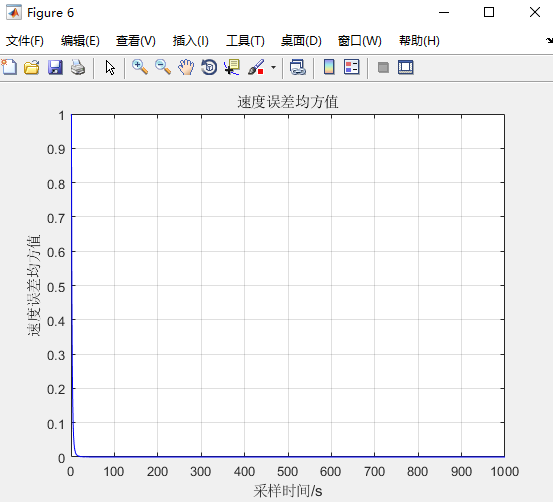
从速度的误差均方值和位移的误差均方值来看，可见kalman滤波对高斯噪声的处理非常有效。
总结：
关于kalman滤波在二维情况下的工作情况，就先这样，如果有那些错的地方还请指正，下次会针对舰船的GPS导航定位系统进行学习和研究。
