《数据结构》03-树1 树的同构

题目

给定两棵树T1和T2。如果T1可以通过若干次左右孩子互换就变成T2，则我们称两棵树是“同构”的。例如图1给出的两棵树就是同构的，因为我们把其中一棵树的结点A、B、G的左右孩子互换后，就得到另外一棵树。而图2就不是同构的。

图

 

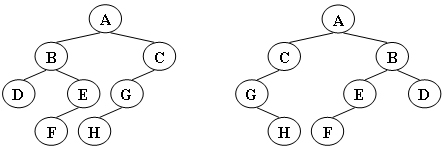
　　　　　　　　　　　　　　图一

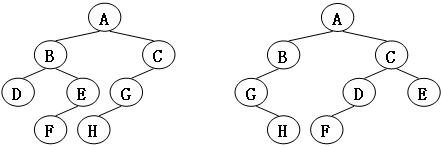
 　　　　　　　　　　　　　　图二

现给定两棵树，请你判断它们是否是同构的。
输入格式:
输入给出2棵二叉树树的信息。对于每棵树，首先在一行中给出一个非负整数N (≤10)，即该树的结点数（此时假设结点从0到N−1编号）；随后N行，第i行对应编号第i个结点，给出该结点中存储的1个英文大写字母、其左孩子结点的编号、右孩子结点的编号。如果孩子结点为空，则在相应位置上给出“-”。给出的数据间用一个空格分隔。注意：题目保证每个结点中存储的字母是不同的。

输出格式:
如果两棵树是同构的，输出“Yes”，否则输出“No”。

输入样例1（对应图1）：

8
A 1 2
B 3 4
C 5 -
D - -
E 6 -
G 7 -
F - -
H - -
8
G - 4
B 7 6
F - -
A 5 1
H - -
C 0 -
D - -
E 2 -

输出样例1:

Yes

输入样例2（对应图2）：

8
B 5 7
F - -
A 0 3
C 6 -
H - -
D - -
G 4 -
E 1 -
8
D 6 -
B 5 -
E - -
H - -
C 0 2
G - 3
F - -
A 1 4

输出样例2:

No

题目分析：

　　先看同构的树有什么特征，虽然左右次序不相同，但他们的子树的值都相同，如图1，A的子树都是B和C，B的子树都是D和E，等等；图2的则不相同，因此他们不是同构，因此判断方式就很明显了，通过判断子树的值来判断是否同构，判断的方法采取递归。然后看看输入样例的结构，为了贴合输入样例，我们使用静态链表（用数组表示的链表），来表示树。每个结点由左子节点，存储的数据（即ABCD·····），右子节点这三部分构成，其中左子节点来表示左儿子的下标，右子节点来表示右儿子的下标。再观察输入样例，发现树的输入是无序的，因此还要找到根的位置，我们很容易想到，除了根以外的结点下标，都会被一个子节点所存储，因此只要找到没有被指向的那个下标，这个下标上的结点就是根结点了。

代码实现：

#include <iostream>
using namespace std;
#define null -1 //结点没有儿子，那么他的左（右）子节点就是空的
#define Tree int
struct TreeNode //树的结点
{
    char data;
    int lchild;
    int rchild;
} t1[10], t2[10];
Tree CreateTree(TreeNode a[])
{
    int n, i, root;
    char left, right; //输入的左右编号可能是'-'，因此用char来存储输入左右编号的输入
    int check[10] = {0}; //用来判断根在哪
    cin >> n;
    if (!n) //结点数为0，返回空树
        return null;
    for (i = 0; i < n; i++)
    {
        cin >> a[i].data >> left >> right;
        if (left == '-')
            a[i].lchild = null;
        else 
        {
            a[i].lchild = left - '0'; //将左右编号的输入转为数字然后存入节点中
            check[a[i].lchild] = 1; //表面这个节点已经被指了
        }
        if (right == '-')
            a[i].rchild = null;
        else
        {
            a[i].rchild = right - '0';
            check[a[i].rchild] = 1;
        }
    }
    for (i = 0; i < n; i++) //判断哪个结点没有被指过
    {
        if (check[i] == 0) 
            break;
    }
    root = i; //将根节点的位置返回
    return root;
}
bool isomorphism(Tree r1, Tree r2)
{
    if (r1 == null && r2 == null) //两树皆空，是同构
        return true;
    if ((r1 != null && r2 == null) || (r1 == null && r2 != null)) //一树空，一树不空，不是同构
        return false;
    if (t1[r1].data != t2[r2].data) //两树根结点的值不同，不是同构
        return false;
    if (t1[r1].lchild == null && t2[r2].lchild == null) //左子树皆空，判断右子树
        return isomorphism(t1[r1].rchild, t2[r2].rchild);
    if ((t1[t1[r1].lchild].data == t2[t2[r2].lchild].data) && //左子树皆不空且值相等，继续判断左子树的子树以及右子树
        (t1[r1].lchild != null && t2[r2].lchild != null))
        return isomorphism(t1[r1].lchild, t2[r2].lchild) &&
               isomorphism(t1[r1].rchild, t2[r2].rchild);
    else                                                      //有空的左子树或是左子树值不相等，那么就判断左子树和右子树的值是否彼此相等
        return isomorphism(t1[r1].rchild, t2[r2].lchild) &&
               isomorphism(t1[r1].lchild, t2[r2].rchild);
}
int main()
{
    Tree r1 = CreateTree(t1), r2 = CreateTree(t2);
    if (isomorphism(r1, r2))
        cout << "YES";
    else
        cout << "NO";
    return 0;
}