【线性代数】第六章 二次型
1.二次型及其标准形
二次型的定义
首先应该知道,二次型是一个关于n个变量x1…xn的一个二次齐次多项式,可以说是一个n元函数式
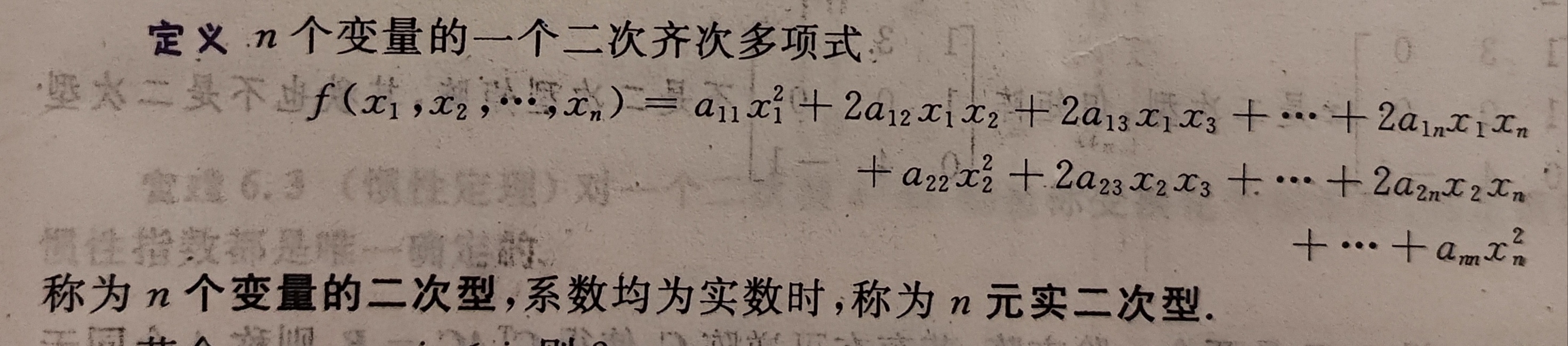
可以看出二次型一共有n(n+1)/2项。
用矩阵形式表示二次型:

对应地可以把以A为对应矩阵的二次型记为x^T A x
根据二次型的式子特性可以看出,式子里的系数只用到了aij(j≥i),即只用到了一个矩阵的上三角部分,所以完全可以用一个对称矩阵A(aij=aji)来表示二次型中的所有系数。
称这个辅助的对称矩阵A为二次型的对应矩阵。
标准形的定义
标准形是一种特殊的二次型,若二次型中只有平方项而没有混合项(或者应该说混合项系数都为0,或者对应矩阵A上除了主对角线上的元素之外都为0),则称此二次型为标准形,又称为平方和。
规范形的定义:
在标准形的定义上进一步取特殊:如果标准形中平方项的系数只有1,-1和0这三种,则称其为二次型的规范形。
记其中系数为1的项的个数为p,系数为-1的个数为q个,系数为0的个数为n-p-q个。
将二次型的混合项系数都设为0,即得到二次型的标准形,再把标准形的平方项系数都设为1,-1或0,则得到二次型的规范形。
正惯性指数和负惯性指数:
二次型标准形中的正平方项的个数p称为二次型的正惯性指数,负平方项的个数q称为二次型的负惯性指数。
二次型的秩:
二次型的对应矩阵A的的秩称为二次型的秩。
合同的定义:
对于两个n阶方阵AB,若存在可逆阵C,使得C^TAC = B,则称矩阵A合同于B
注意合同与相似的区别,矩阵相似指的是P^-1AP = B,注意相似是逆矩阵。而矩阵合同如上所示是转置矩阵。
矩阵合同的性质:
1.反身性,即矩阵A与其本身合同
2.对称性,即A合同于B,则B也合同于A。(因为矩阵C是可逆矩阵)
3.传递性,即A合同于B,B合同于C,则A合同于C。
(合同矩阵的惯性指数是相同的,所以可以求二次型的惯性系数直接看其对应矩阵的主对角线系数即可)(这条性质待定,书里没有直接提到过)
矩阵合同与矩阵相似的比较:
矩阵相似指的是P^-1 AP = B,它其实指的是矩阵A能通过初等变换得到矩阵B,当矩阵相同时,两者有相同的秩和特征值。
矩阵合同指的是P^TAP = B,它的引入是为了表示这些矩阵可以在使用不同未知数体系的情况下作为同一个二次型的对应矩阵。(二次型的坐标变换其实就是用一个合同的矩阵来代替原来的对应矩阵)所以可以得知两个合同的矩阵的正负惯性指数一定相同。
(二次型的正负惯性指数与金融分析中的应用有关,如股市预测,在这里就不深入研究了)
二次型中的坐标变换的定义:
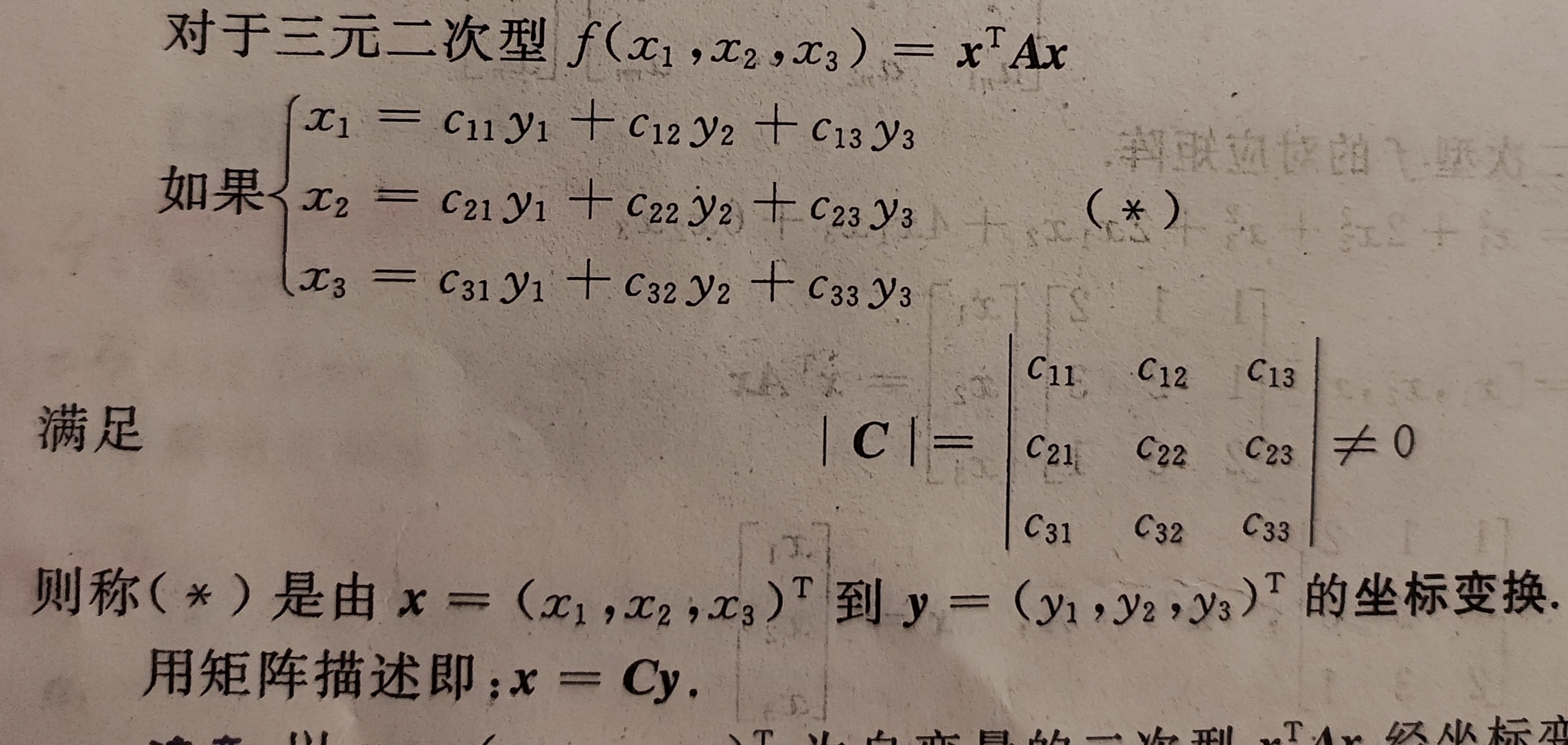
即将二次型中的各个变量Xi用另外一套变量Yi代替。
需要注意的是,在转换中x与y的联系矩阵C的行列式不能为0。
坐标变换后的效果:
容易知道,经过x = Cy坐标变换后,原来关于x的二次型就变成关于y的了,而这里的对应矩阵也会有所变化:
原二次型为x^TAx = yT(CTAC)y = y^T B y,即坐标变换到Y之后,二次型的对应矩阵为B = C^T A C。
并且这里可以得到一个信息:原对应矩阵A与现在的B之间是合同的。
正交变换:
如果在坐标变换x = Cy中,矩阵C同时又是正交矩阵(CC^T = C^TC = E),则称其为正交变换。(又可以看出正交矩阵其实就是逆矩阵等于其转置的矩阵。)
通过坐标变换将二次型化为标准形(除主对角线外其他系数都为0):
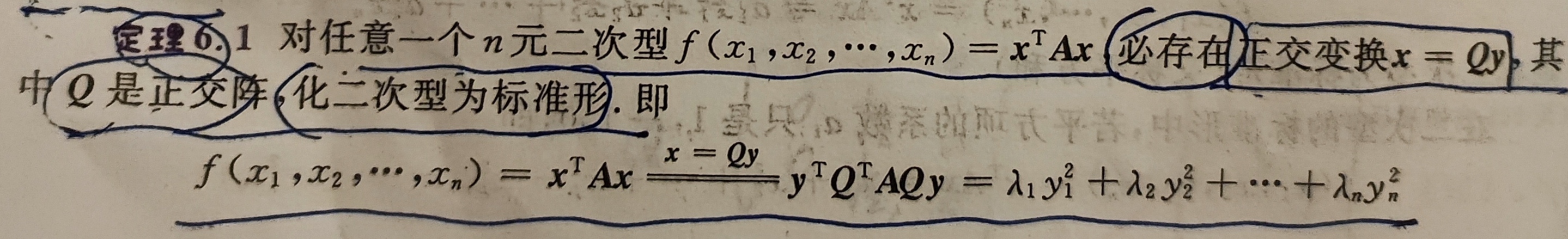

经过正交变换化为标准形后,平方项的系数即为原对应矩阵A的特征值。
借助可逆矩阵C将二次型化为标准形:

其原理是,对于n阶实对称矩阵,必定存在可逆矩阵能能将该矩阵对角化。
关于二次型化为标准形的惯性定理:
对一个二次型坐标变换化为标准形,则其正惯性指数和负惯性指数都是唯一确定的。

先按一般步骤求出特征向量,如果是一个特征值对应一个特征向量的情况,则不需要正交化,只需要把各个特征向量单位化即可;如果存在多重的特征值,则再用施密特正交化对特征向量进行处理(施密特正交化即为先正交化再单位化))
将这些处理后的向量拼接起来即为正交变换中的矩阵Q
计算步骤:
1.配方法化二次型为标准形
根据二次型的式子,将式子尽量化为(a1x1 + b1x2 + c1x3)^2 + (a2x1 + b2x2 +c2x3)^2 +……的形式即可,理论上任意一个二次型都是可以成功配出平方的。

在上面的图中可以看出,只要稍作改动,将标准形中的系数放入平方内部,就可以使所有平方项的系数都为1或-1,所以通过配方法也可以将二次型化为规范形。
2.正定二次型
正定二次型的定义:
正定二次型就是如果无论未知数xi取何值,二次型的值都>0,则此二次型为正定二次型。并将其对应矩阵称为正定矩阵。

相关定理:
1.可逆线性变换不改变二次型的正定性。
可逆线性变换在这里指的就是对二次型的对应矩阵做初等行/列变换。
2.二次型正定的充要条件

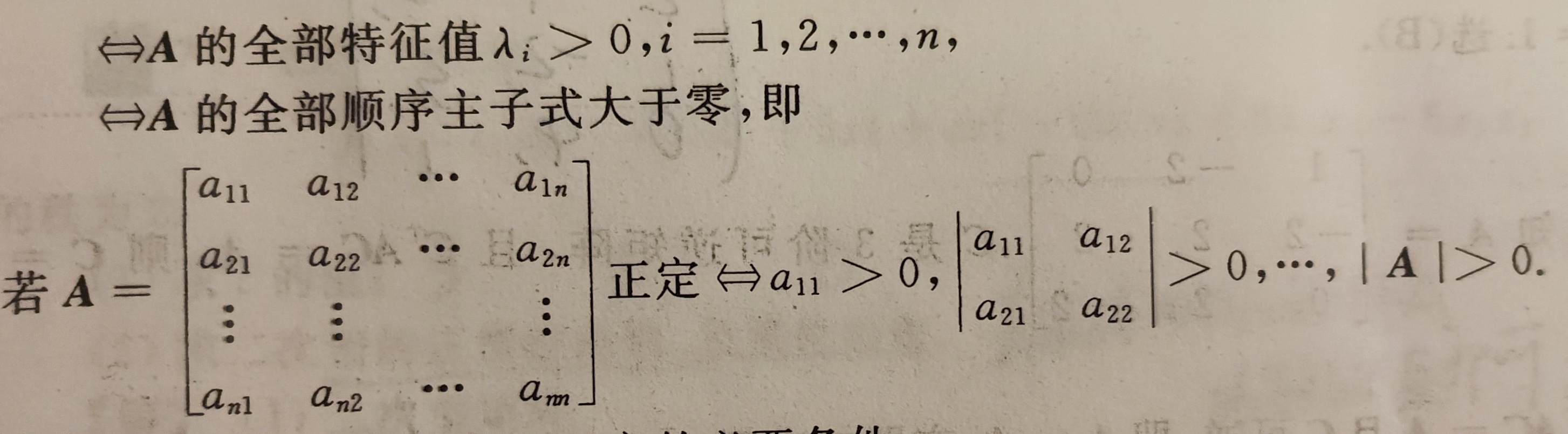
1.f正定等价于对应矩阵A的正惯性指数等于n,即矩阵A的所有特征值都为正
2.f正定 等价于 对应矩阵A与单位阵E合同
3.这个和第2条其实是同一条,因为合同可以交换,所以E也合同于A,即存在可逆矩阵D,使得D^TED = D^TD = A
所以f正定 等价于 对应矩阵A可以表示为D^TD的形式
4.这一条与1是同一条,矩阵A的正惯性指数等于n,自然而然地也就有A的所有特征值都为正
5.等价于矩阵的全部顺序主子式都大于0
(补充:顺序主子式即为:取矩阵A的前i行前i列,这个部分矩阵的行列式即为顺序主子式。)
这里还要注意,反过来说的话就是:只有当矩阵A的所有顺序主子式均大于0时,才能推出二次型正定。
(这也就是为什么在下面的讨论中,矩阵A的行列式大于0是二次型正定的必要条件而不是充要条件。)
3.二次型正定的必要条件
(即根据二次型正定能导出哪些信息)
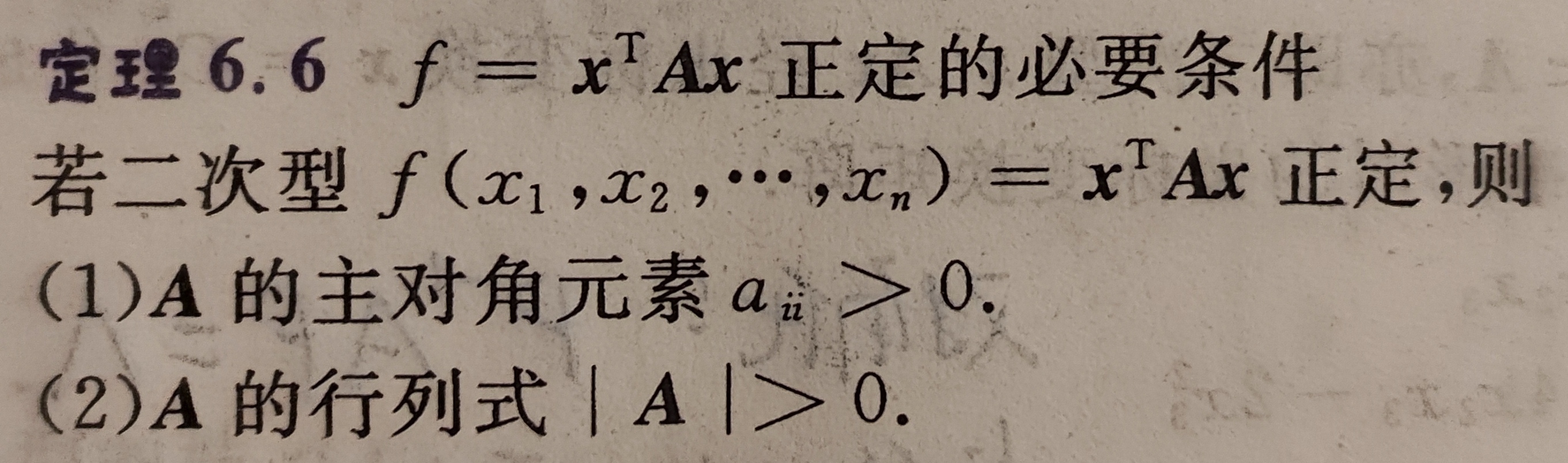
若二次型正定,则有:
对应矩阵A的主对角元素都大于0
矩阵A的行列式也大于0
补充:如果矩阵A是正定矩阵,则A的伴随矩阵A* 也是正定矩阵。

