【数据结构】B树和B+树

这部分内容较少，B树要理解基本特性，掌握其建立、插入和删除操作；B+树只需要掌握基本概念即可

1.B树及其基本操作

b树是在平衡二叉树的基础上的衍生概念
（1）B树的定义：m阶B树即为所有结点的平衡因子均等于0的m路平衡查找树
复习：m叉树指的是结点的最大子树数目，而不是说m叉树的每个非叶结点都必须是m叉的


解释：
1.这里先记住B树每个结点最多有m棵子树即可，关于每个结点的关键字个数问题在下面会解释
并且m阶B树中的m指的其实就是每个结点的最大孩子个数。
2.这里说的比较含混（这书写的什么b玩意），根节点不是叶结点指的是根节点中有关键字，即这条定义可以描述为下面这样：
如果根节点没有关键字，则这个根节点下面不会有子树，整个B树为空；如果根节点中有关键字，则其子树个数必然≥2。（这里是因为子树个数等于结点关键字个数+1）
3.这个就是B树的定义要求，因为B树是建立在平衡二叉树的基础上的，所有非叶节点必须都有一定数量的关键字和子树，这就使得B树的平衡性在一定程度上得到了保证。
4.非叶节点的结构如图所示，
第一项是这个结点中关键字的个数n.
后面即为交替排列的关键字和子树
对于每个关键字K，其左右两边都必须有子树P，两个关键字之间只能有一棵子树。也就是说当结点中有n个关键字时，对应地就有n+1棵子树。
并且子树和关键字之间是这样的关系：关键字K左侧的子树中所有结点的所有关键字都小于K，右侧子树则所有关键字都大于K。
5.叶结点都用外部结点（只有定义不携带关键字），并且所有叶结点都在同一层上。这也对应了上面的B树的定义，即B树中所有结点的平衡因子都等于0.
这些结点代表的意义是待查数据不在查找表中，查找表失败。
在B树中，讨论树高和树的结点个数时，都不考虑最底层的外部叶结点


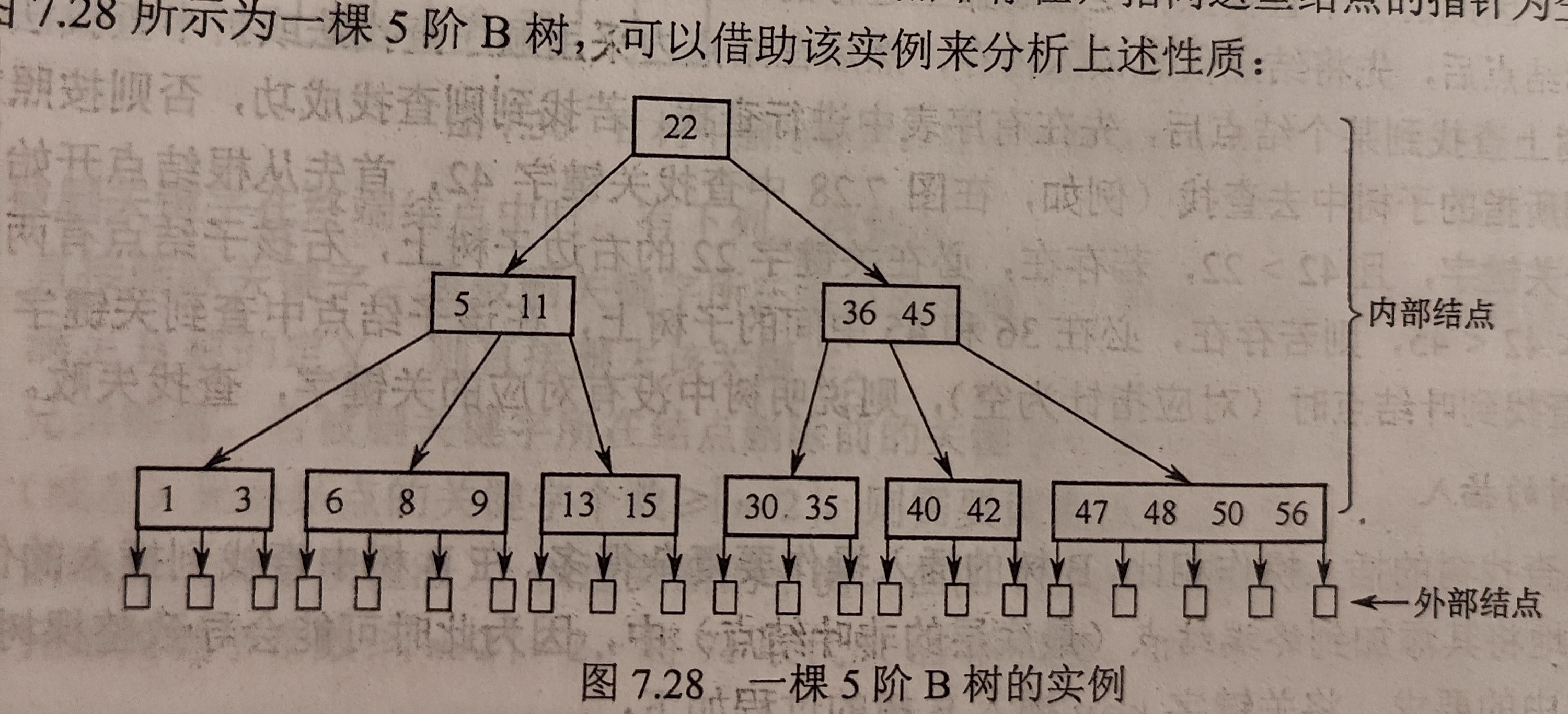
对B树树高的分析
B树的查找效率和操作效率与其树高有关

2.B树的查找

（简单）

3.B树的插入

插入分为三步进行：
定位：找出插入该关键字的结点位置，容易知道新插入关键字时插入位置一定是最底层中的某个非叶节点。
插入：在结点内部的有序表中查找插入位置，并先插入。
分裂结点：如果插入后结点内的关键字个数大于了m-1(由于关键字是一个一个插入的，所以当需要分裂结点时结点内的关键字个数一定是m)时，为了保持B树的定义，需要对这个结点进行分裂，具体分裂方法如图所示。
以下是从零开始把查找表插入空B树的过程：

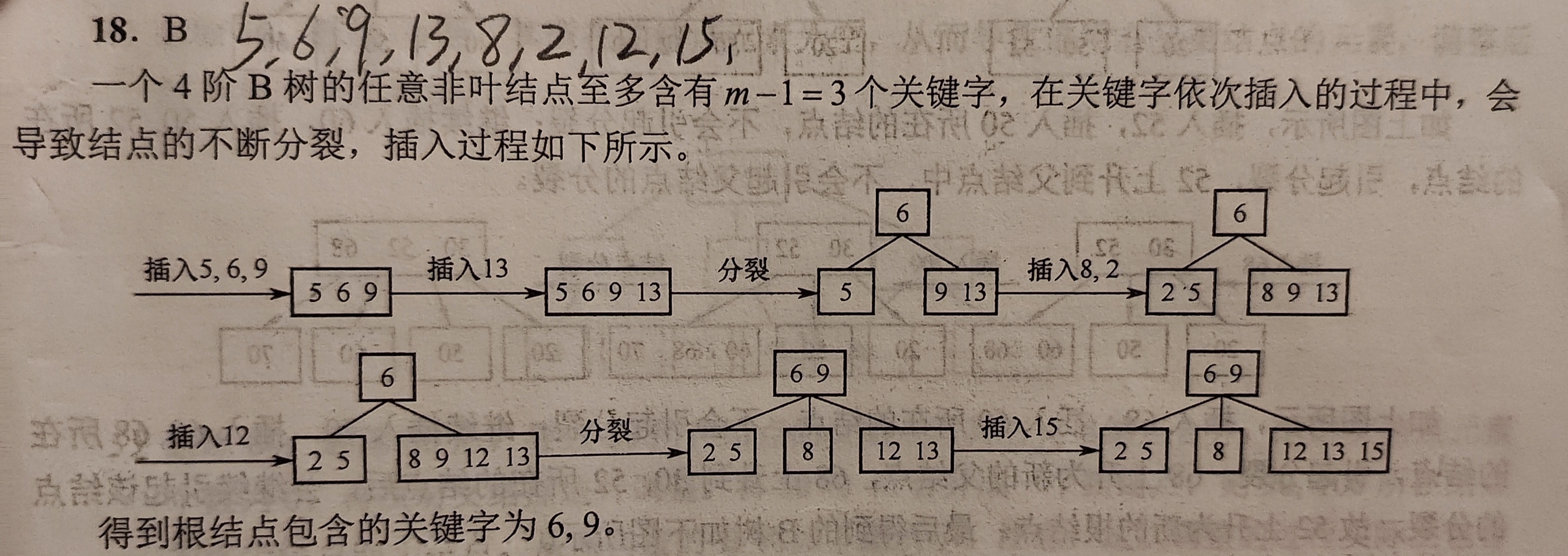
4.B树的删除

与上面的插入过程相反，由于B树结点中关键字个数的限制为⌈m/2⌉-1 ≤ 个数 ≤ m-1
从节点中删除关键字时，关键字个数可能会小于⌈m/2⌉-1，这时为了保持B树的定义就需要进行一定的后处理（合并）
（从B树的定义可以得知，其结点结构是关键字与子树指针交替排列，所以删除一个关键字后必须对这个空缺进行调整，使之重新满足B树的定义）

情况1：如果被删除关键字不在终端结点中，则可以用k的前驱或后继关键字k'顶替上k的位置，再对k'抽走后形成的空缺进行处理。
用上面这种方法就能最终使待删除位置处于终端节点中，由此将情况1统一进删除关键字在终端结点的情况。

（这里的前驱或后继指的是这个关键字在本结点中的前驱或后继，所以每次只需要向下找一层即可。并且因为整个B树的最小关键字和最大关键字一定在终端结点中，所以这个情况中的关键字k一定有其前驱和后继）

情况2：被删关键字在终端节点中时，有以下三种情况：

（首先注意，终端结点的结构是关键字与外部结点交替排列，即因为他处在最后一层，所以其所有子树都是空结点，所以在这里删除关键字也不会打破结点结构，只需要删除一个多余的外部结点即可，在这里删除关键字唯一会导致的问题只有关键字的个数不符合定义要求）

（不用死记硬背，做几个题就行了）

4.B+树的概念

B+树是对B树的变形，是应数据库所需出现的概念。

m阶B+树的定义：
（1）每个分支结点最多有m棵子树

只需要了解B+树的定义规则即可，根据讨论B树的思想，B+树的相关操作和性质都很好理解，都是借助树形结构提高查找效率并且通过控制树的平衡性来进一步控制平均查找效率。