数据结构查找红黑树查找

1.红黑树的定义

红黑树可以看作是对平衡二叉树的进一步改进。平衡二叉树的一个缺点在于插入和删除操作中为了维持平衡会消耗很大的执行代价，降低效率。红黑树的结构是在平衡二叉树的平衡标准上稍微放宽得到的。

红黑树的定义：

（红黑树的引入其实是在234树的概念上的延伸，红黑树其实完全就是234树的二叉树版本）
补充概念：二叉树的旋转

我的理解方式比较土，从字面意义上理解为旋转即可（旋转后为了保持二叉树结构，对子节点进行一定的调整）
右旋示意图：

左旋示意图：

总结下来就是：右旋的话就使根节点的左孩子成为新的根节点，左旋的话就使根节点的右儿子成为新的根节点。

从定义解释红黑树的优点：
黑高的概念：从某个
结点出发到一个叶结点的任意一个简单路径上的黑结点总数称为该结点的黑高。（根据红黑树的定义）
根节点的黑高即为这个红黑树的黑高。
（1）在红黑树中，从根节点到叶结点的最长路径不大于最短路径的2倍。
这条结论控制了红黑树的查找效率在一定范围内。
这条结论可以从红黑树的定义中推出：不存在两个相邻的红结点。
从根节点到叶结点：最短路径一定是全部由黑结点构成的路径，最长路径一定是红黑相间的路径。所以可以得出上面的结论。
（2）有n个结点（内部结点）的红黑树的树高h<2log2(n+1)
外部结点指的是为了便于实现而添加的空叶结点。内部结点指的就是查找表中的关键字的结点。

总结：红黑树用一定程度上保证其平衡性（左右子树高度相差不超过2倍）取代了平衡二叉树的绝对平衡。在实际中应用范围更广。

2.红黑树的插入

红黑树的插入过程仍然和二叉排序树的过程大致相同，但是插入新节点之后需要通过重新着色或者旋转操作进行调整，以满足红黑树的性质。
首先，由于需要保持红黑树上每条路径上黑结点个数相同，所以新插入结点时，都插入为红结点（这样在调整时也比较简单）。
插入过程中的调整一般都是为了使定义中的5得到满足，即使每个结点到任意一个叶结点的简单路径上所含黑结点的数量相同。

插入过程：
上面已经讨论过，在新插入结点时，先将其着色为红色。

上述为不需要调整的两种情况：
1.新插入结点的父节点颜色为黑色
2 新插入的节点即为根节点，这时只需要把这个新结点着色为黑色，不需要做更多的调整
这时能够满足红黑树的定义，不需要调整

接下来讨论结点z既不是根节点，其父节点也不是黑结点的情况：

当z的叔结点是黑结点的情况：

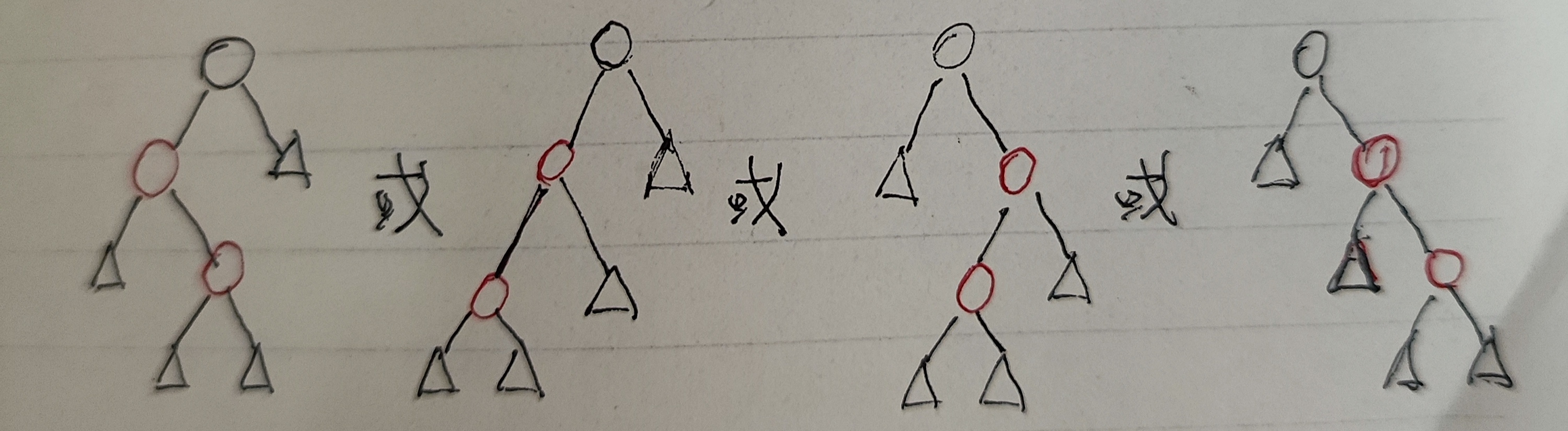
第一类：z.p是z.p.p的左孩子的情况
这里的z.p代表z的父节点，z.p.p代表z的爷结点

这种类型又分为两小种情况：
1 结点z是其父节点的右孩子
如图，现在的问题是两个红结点相连，并且如果直接把新结点变成黑色的话又会使性质5不符合
对其处理方法是对z.p为根节点的子树进行左旋，将其转换为情况2
2 结点z是其父节点的左孩子（如上图中所示）
对其处理方式是对以z.p.p为根节点的子树进行右旋
处理之后的结果如图所示即为符合定义要求的红黑树
总结：情况1按LR(先左旋后右旋)，情况2按LL(右单旋)

第二类：z.p是z.p.p的右孩子的情况
这种情况的处理方式可以类比第一类的方式
其下也包括两种小情况：RL（先右旋后左旋）和LL（左单旋）（做题时理解一下即可，这里不再赘述）

当z的叔结点是红结点的情况：
这种情况下不必再区分z是左孩子还是右孩子，并且由于定义中3的限制(即虚拟叶结点都是黑色的)，可以得知z的叔结点不是虚拟的节点
所以现在的问题只剩下两个红结点相邻

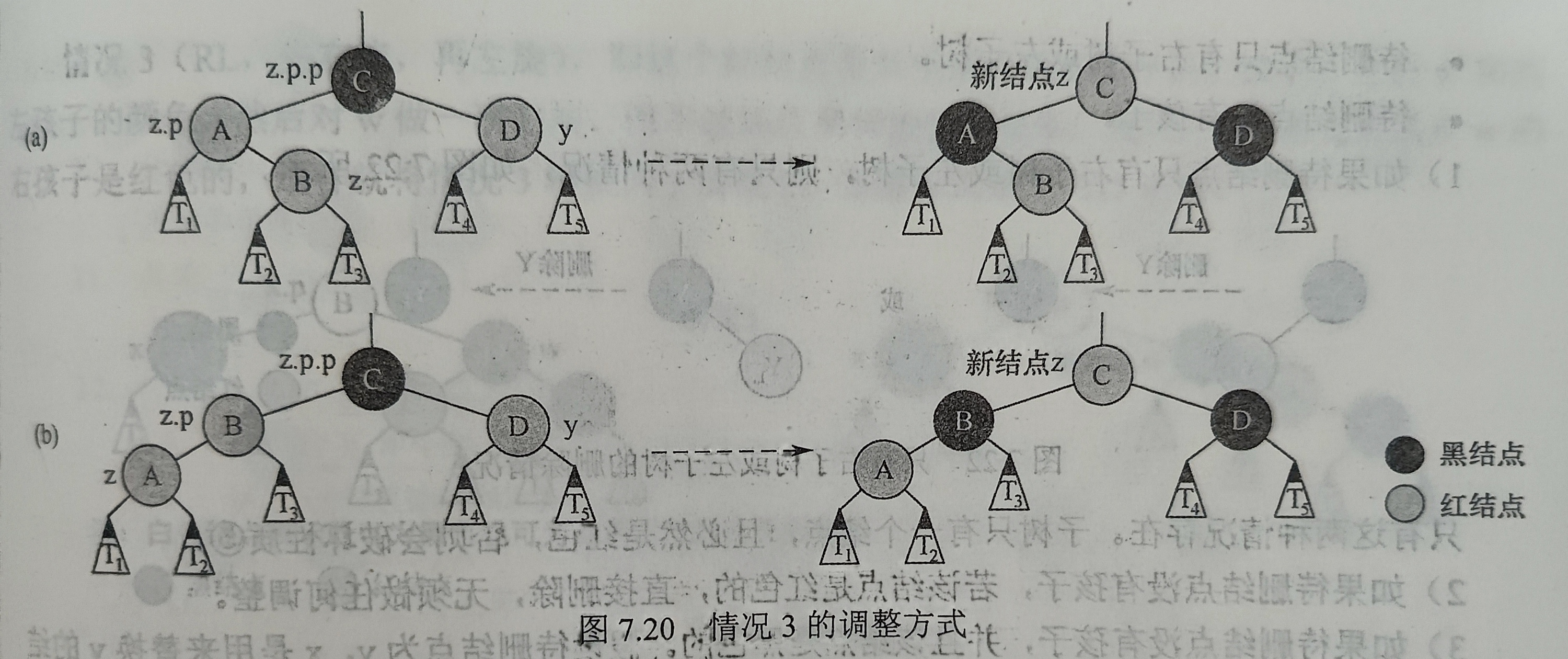
可以看出与z的叔结点为黑结点不同的是，z.p.p与其两个子节点形成了对称的颜色，可以根据这个特点直接调整颜色来使性质4和性质5符合，但是其问题在于在调整后z.p.p的子树范围内符合了定义，但是z.p.p的颜色改变会使上面的部分不符合定义，所以现在下一步应该做的是将z.p.p作为新的z向上分析，对上面的部分进行调整。

在这些插入操作中始终要注意几点：
1，红黑树的定义中有虚构结点，并且必须为黑结点，如果一个树没有虚构结点，则要加上
2，在上面的分析中，都是把结点z当成新插入结点来分析的，在这些情况中z一定为叶结点，但是由于情况3中需要把z.p.p重新当成z向上调整，所以这三种情况中都有可能出现z不为叶结点的情况