数据结构 查找 树形查找
1.二叉排序树
二叉排序树可以提高查找、插入和删除的效率。
(1)二叉排序树(BST)的定义

定义比较简单,左子树所有结点<根节点<右子树所有结点
同时左右子树也分别都是二叉排序树
特点:对二叉排序树进行中序遍历,可以得到一个递增有序序列。
(2)二叉排序树的插入
BST的插入是为了其构造而使用的一个操作
给定的查找表不会直接给出BST的树形结构,而是给出一个线性的序列,所以在使用BST进行查找时,要先根据原始的线性查找表构造出BST的树形结构,这个过程的方法就是将关键字按二叉排序树的定义挨个插入到树中。
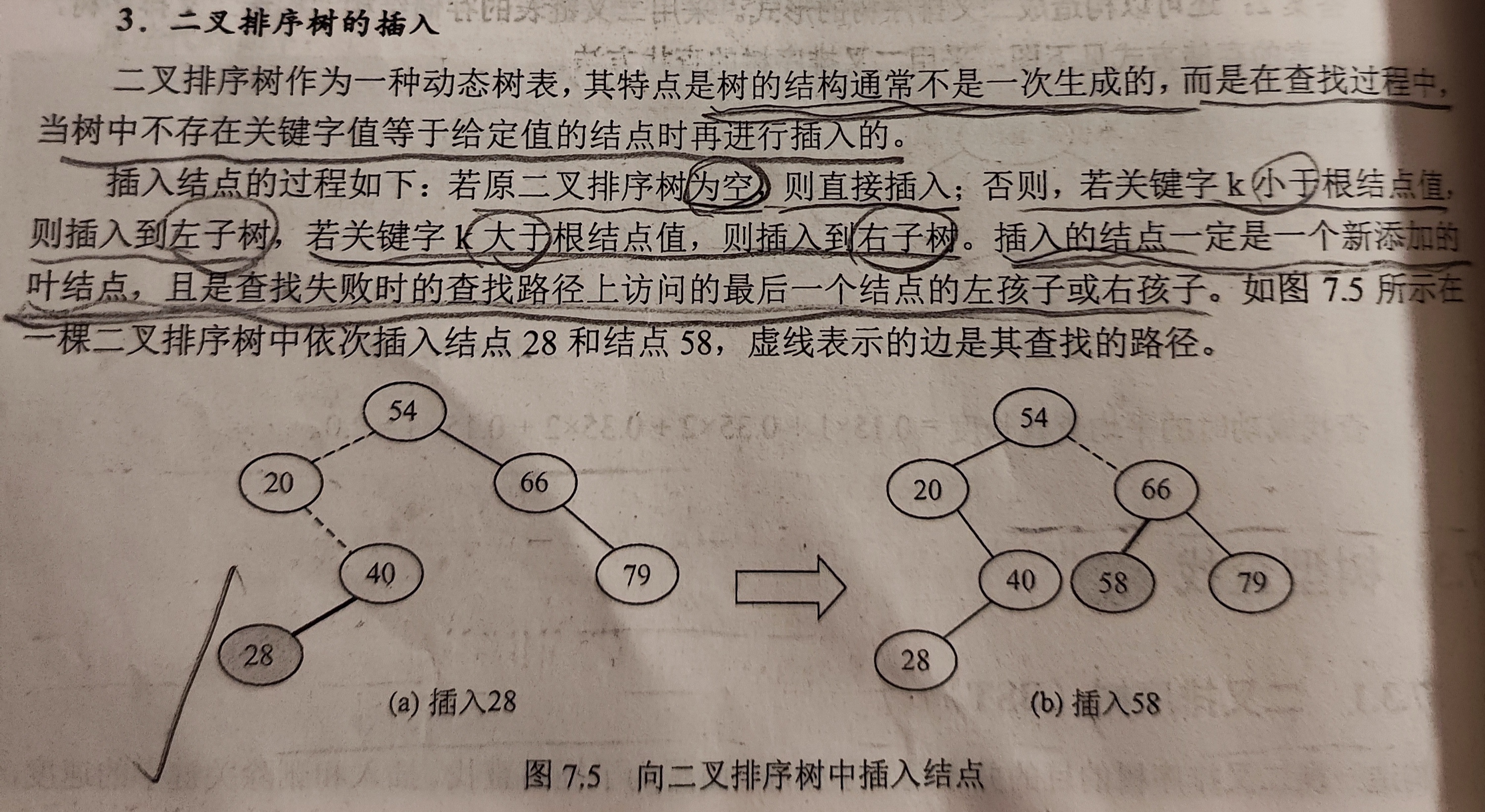
插入方法就是:
当树为空时,直接插入;当树不为空时,将待插入关键字逐层与根节点的值进行比较,如果待插入关键字小于当前根节点,则向左子树深入;反之则向右子树深入。直到到达最后一层,将这个关键字插入为BST的一个新的叶结点。
BST的插入算法是一个递归算法。
(3)二叉排序树的删除
删除某个结点分为两种情况,当删除的节点为叶结点时,则直接删除;否则需要用其子树上的结点进行重新连接。

删除非叶节点时,如果这个节点的左/右子树为空,则直接把另一边的子树替补到当前位置即可,比较简单。
如果该结点的左右子树都不为空,则需要找到其右子树上最小的节点k(即右子树中序序列中第一个结点)。用结点k替补到当前位置后,还需要对结点k进行删除操作。
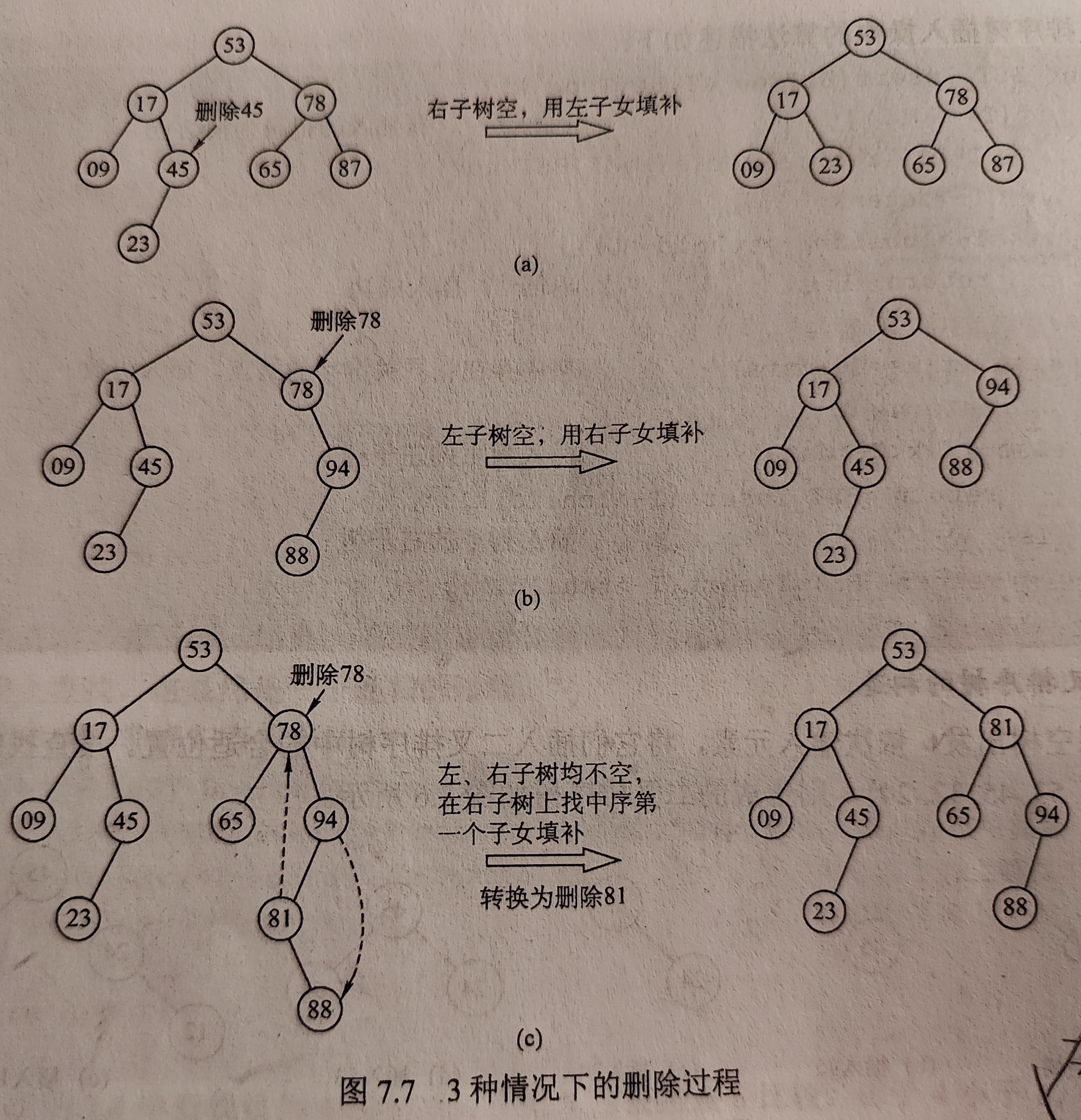
(4)二叉排序树的查找效率分析。

(注意二叉排序树与二分查找的对比)
其查找效率受到树高的影响
在平衡二叉树的情况下,平均查找长度为O(log2n)
在最坏的单支树的情况下,平均查找长度为O(n)
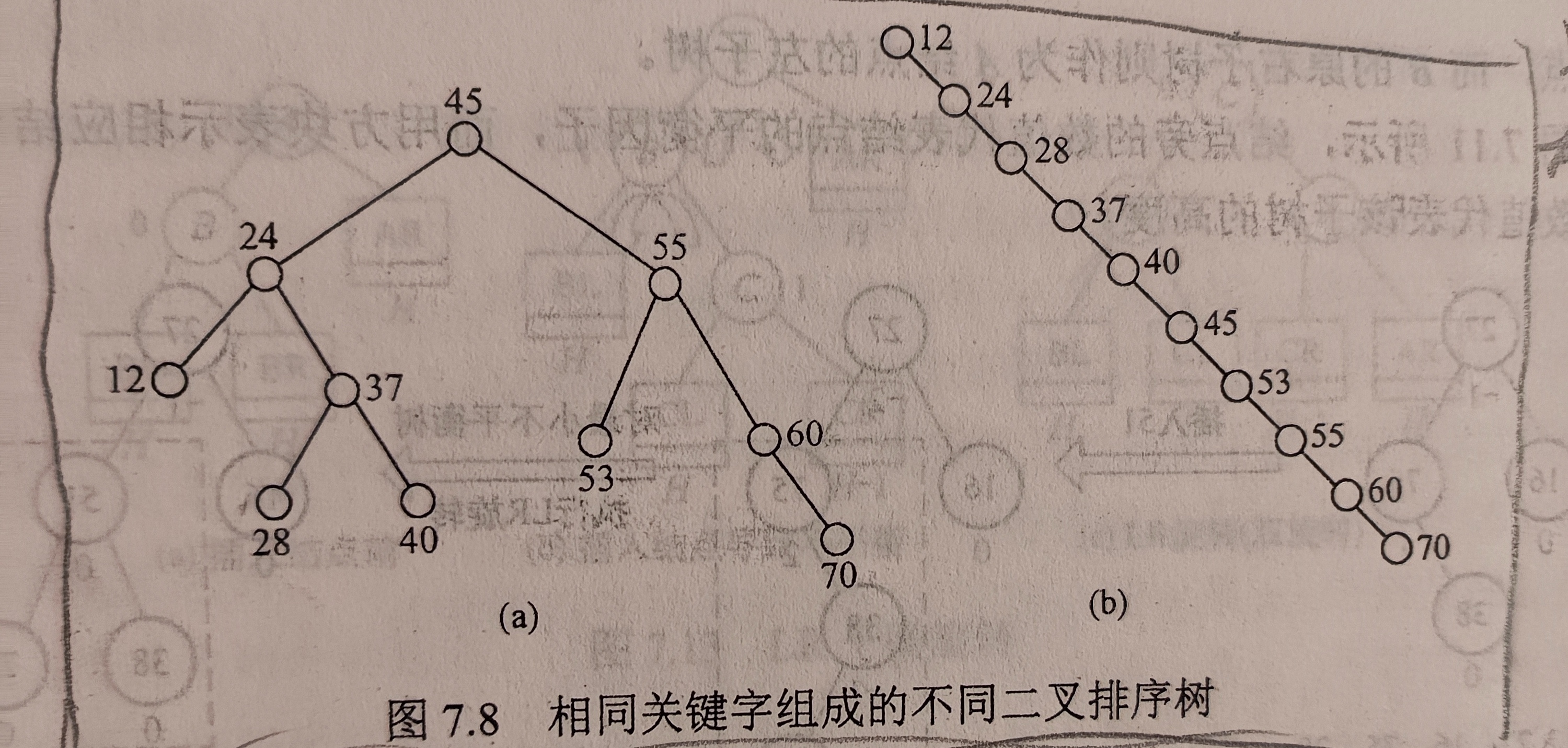
2,平衡二叉树
平衡二叉树是一种特殊的BST,为了提高BST的查找效率。
(1)平衡二叉树(AVL)的定义

有两个需要注意的点:
1.对于任意一个结点,其左右子树的高度差不超过1。(这里的树高指的是树的根节点与最底层的根节点之间的高度差。)
2.平衡因子的定义:树中某个结点的左子树与右子树之间的高度差。平衡因子的值只可能是-1,0,1这三个值,出现其他的值则说明二叉树不再平衡了。
(2)平衡二叉树的插入
平衡二叉树的插入问题其实是:
如何在构造平衡二叉树的插入过程中始终保持树的平衡性?
解决思路:每插入一个结点首先检查其插入路径上是否出现不平衡(这个是通过每次插入结点后随即更新各节点的平衡因子来实现的);如果导致了不平衡,则找到最近的平衡因子大于1的节点,对各结点的位置关系进行调整,使之恢复平衡。
最小不平衡子树的概念:

容易看出:新插入的结点与不平衡节点之间只会有三层结点
如何对最小不平衡子树进行调整?
把调整的情况分为4种:LL,RR,RL,LR.
这些情况是根据新插入的结点与不平衡节点之间的路径形状来区分的
1.LL调整
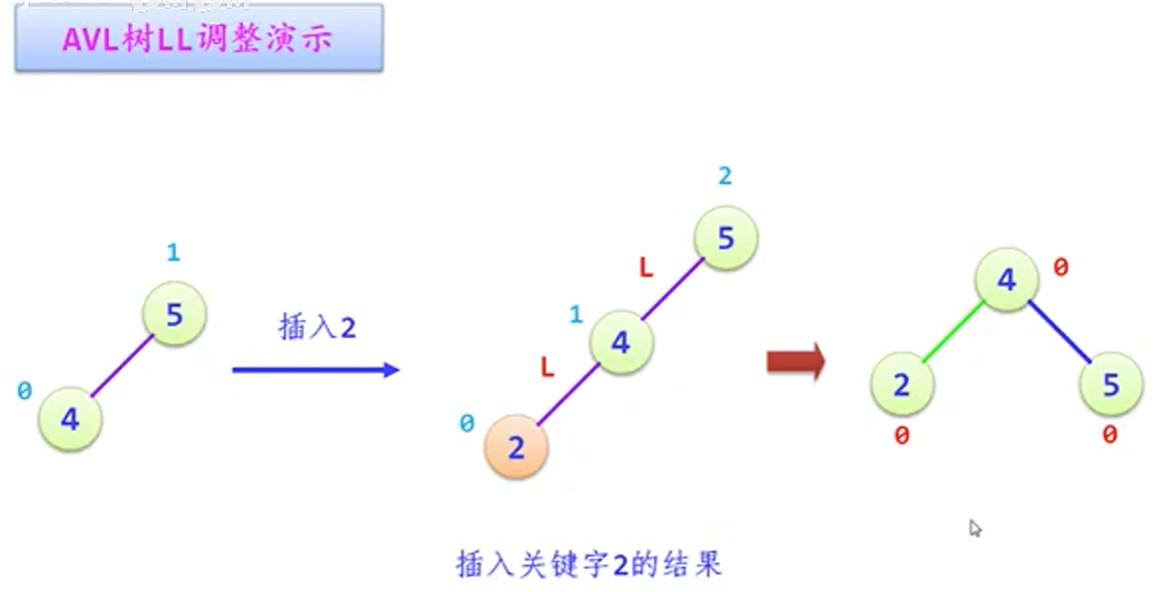
把较长的单支树调整为三角形的树。(当然只在最小不平衡子树中)
2.RR调整
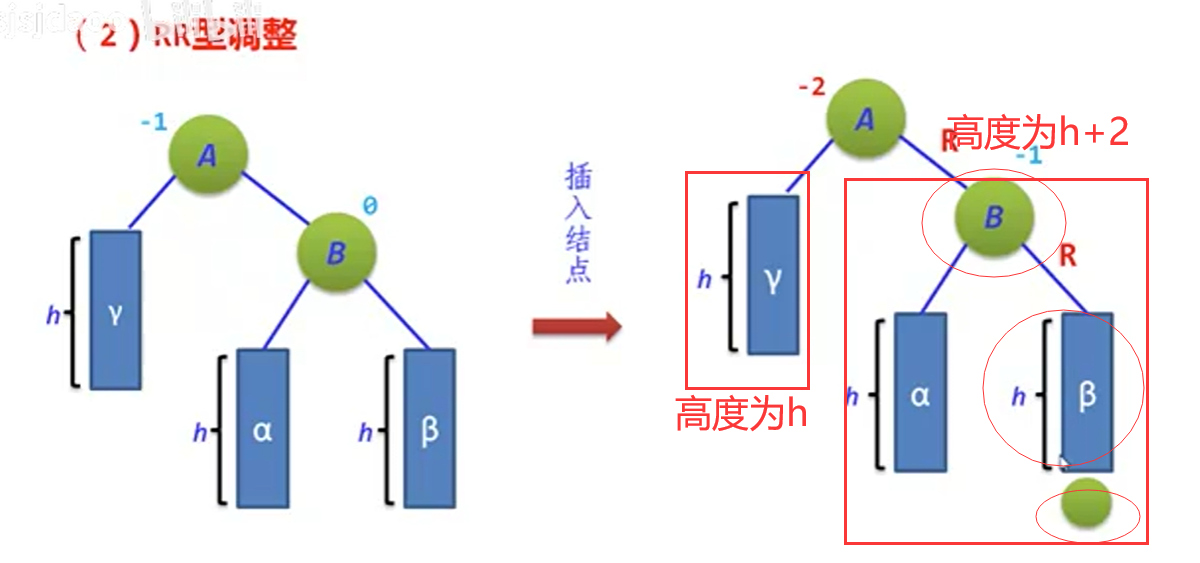
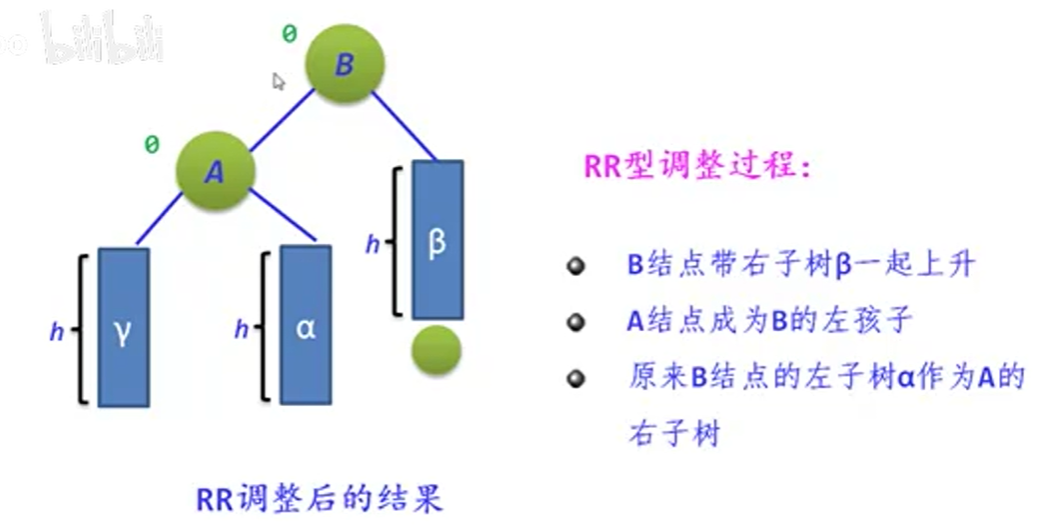
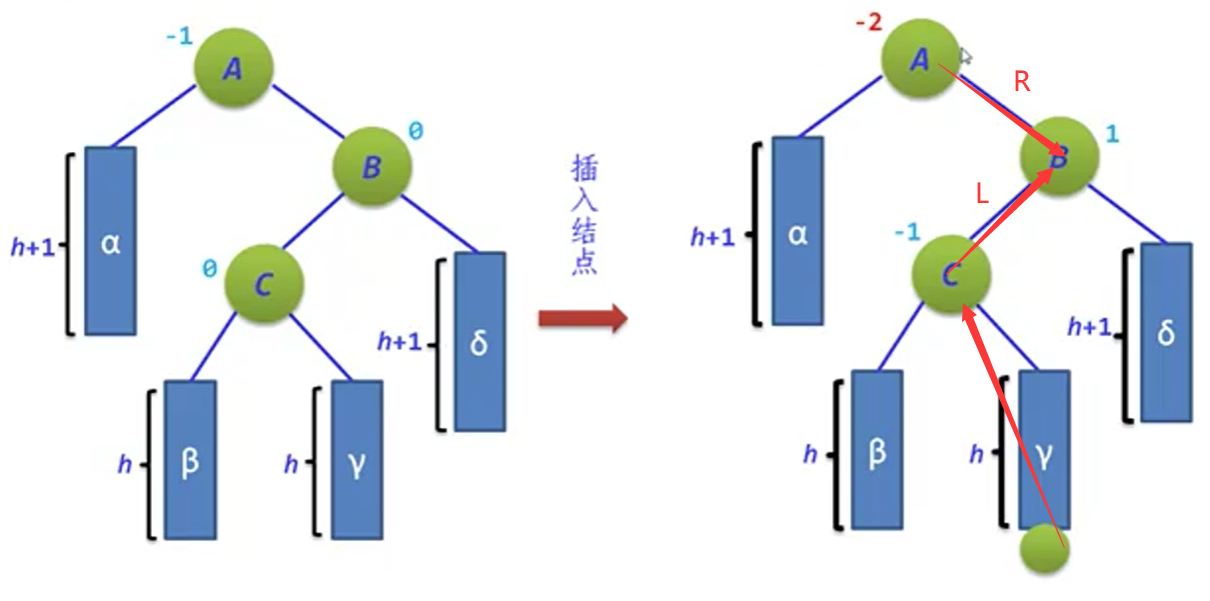
这里的上移部分是:新加入的结点到不平衡结点(A结点)之间的路径。
示例:

3.LR调整
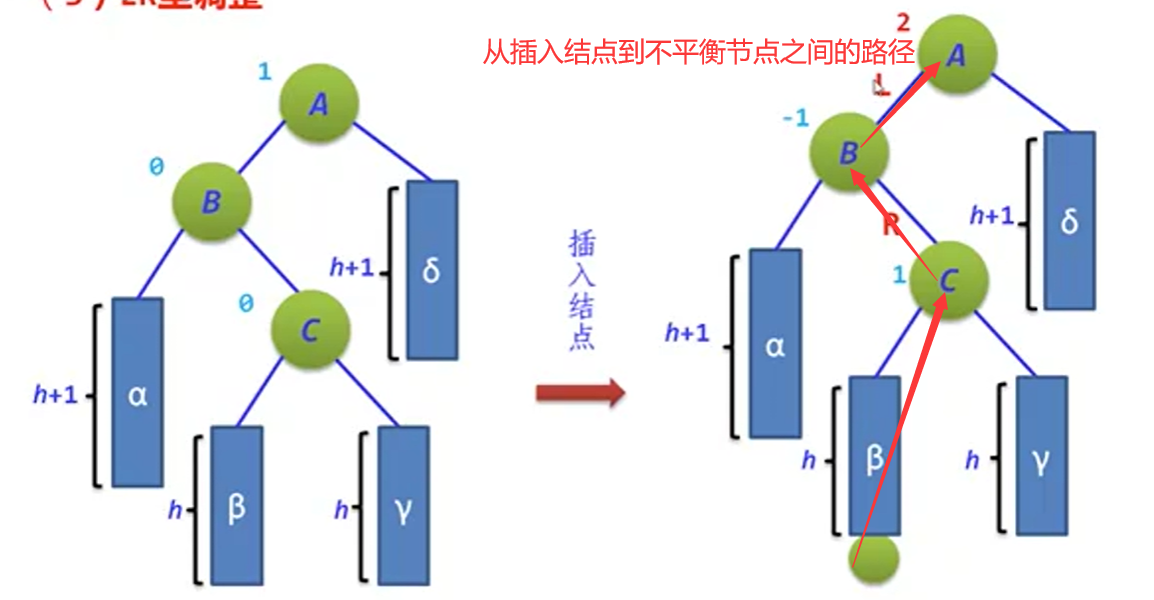
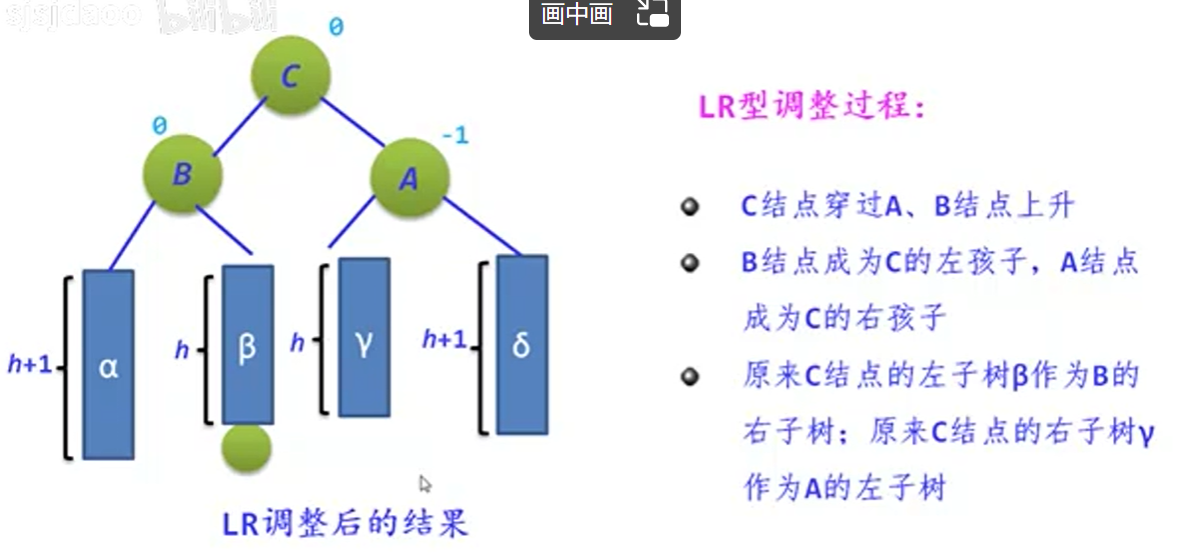
顺序可以描述成这样的过程:
c结点上升为A和B的父节点
c的左子树连接到B的右子树上
C的右子树连接到A的左子树上
示例:
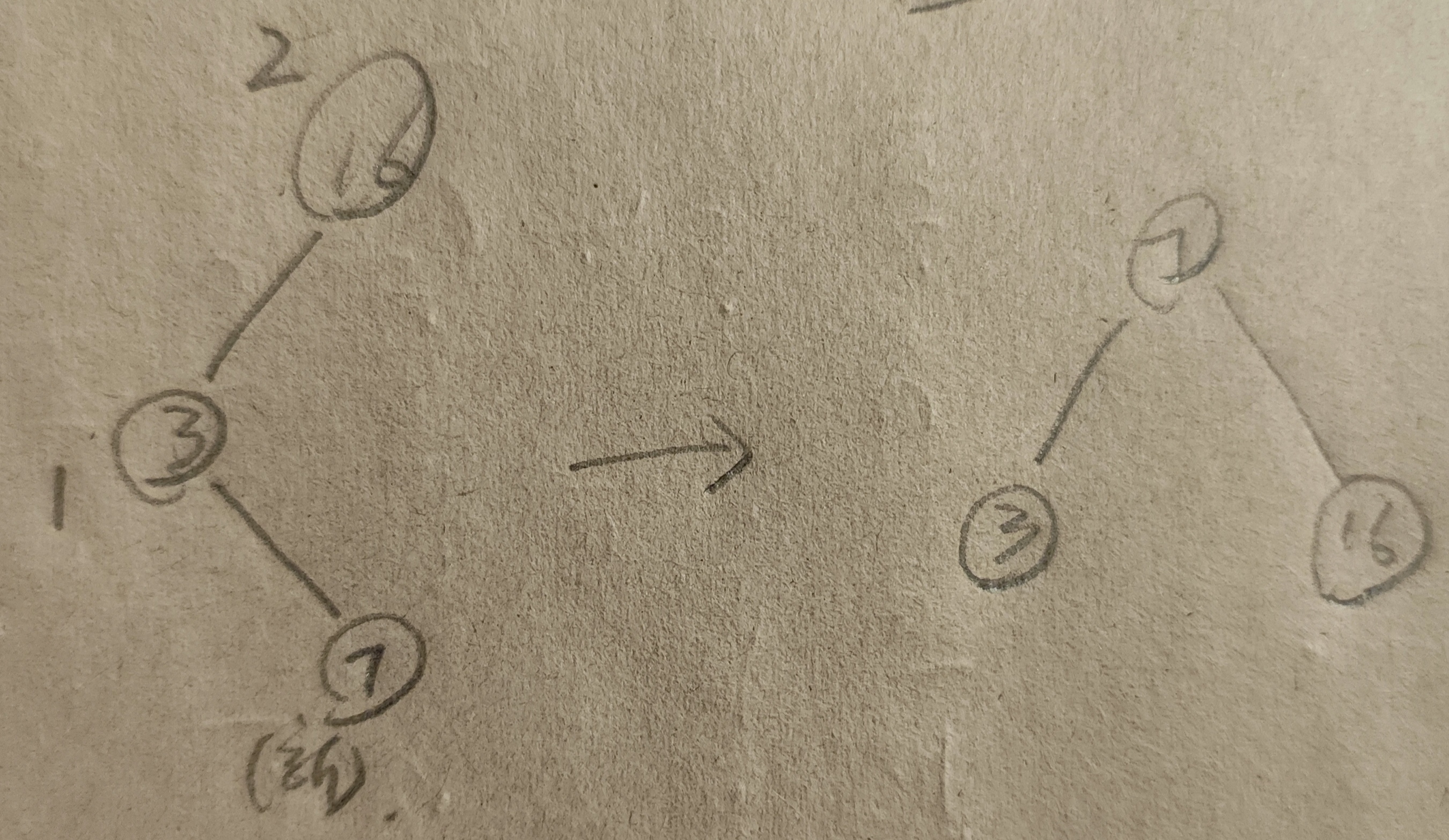
4.RL调整
调整策略与LR调整的策略类似
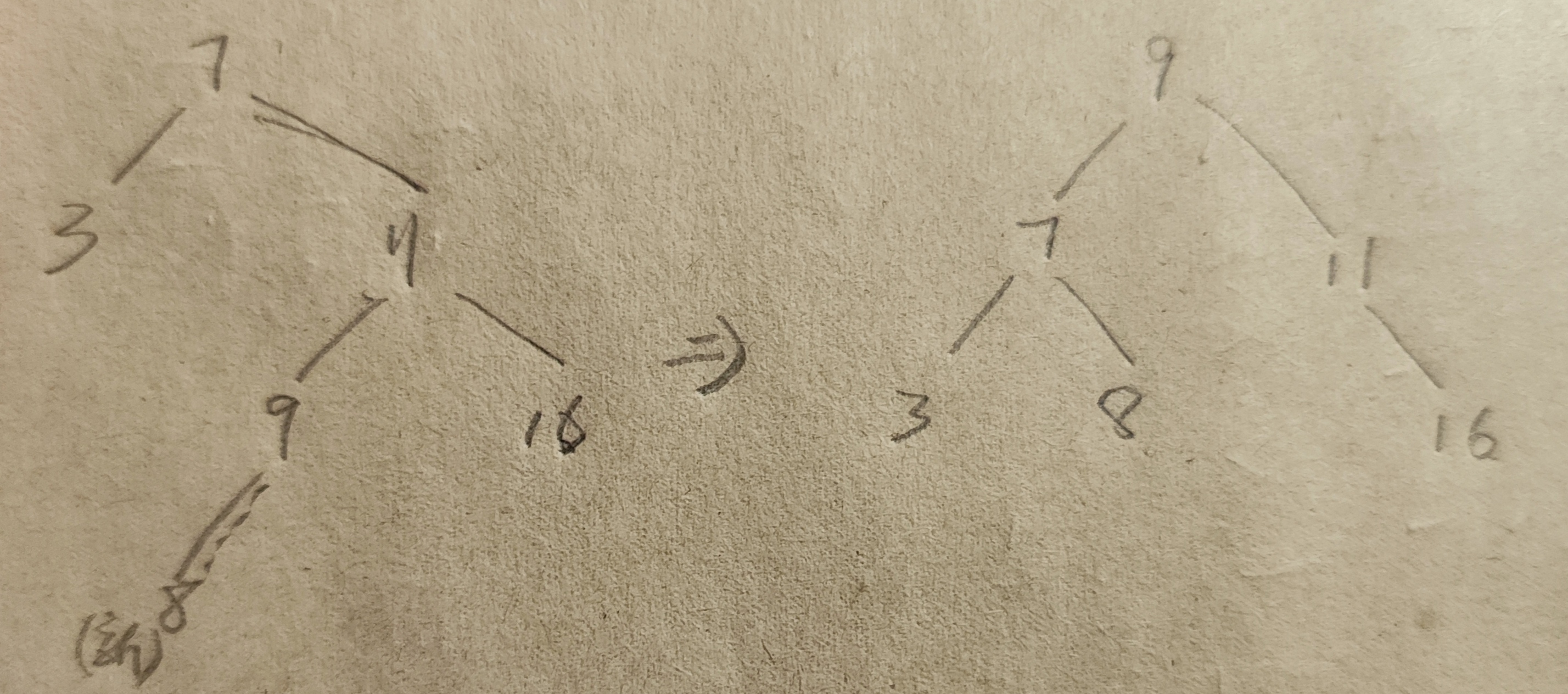
3.平衡二叉树的删除
删除的过程与结点插入的过程基本相同,也是先直接插入,再对不平衡的部分进行调整。

(做题时再慢慢学)
4.平衡二叉树的查找
平衡二叉树本质上是一种特殊的二叉排序树,只对二叉排序树的树高加以限制。所以AVL的查找过程和二叉排序树的查找过程完全相同。
含有n个结点的平衡二叉树的平均查找长度为O(log2n).
(意思就是给出的查找表的长度为n)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号