[Acwing1250] 格子游戏

[Acwing1250] 格子游戏

• 并查集

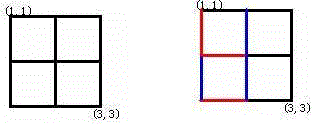
Alice和Bob玩了一个古老的游戏：首先画一个 \(n×n\)的点阵（下图 n=3）。

接着，他们两个轮流在相邻的点之间画上红边和蓝边：

直到围成一个封闭的圈（面积不必为 1）为止，“封圈”的那个人就是赢家。因为棋盘实在是太大了，他们的游戏实在是太长了！

他们甚至在游戏中都不知道谁赢得了游戏。

于是请你写一个程序，帮助他们计算他们是否结束了游戏？

输入格式

输入数据第一行为两个整数 \(n\) 和 \(m\)。\(n\) 表示点阵的大小，\(m\) 表示一共画了 \(m\) 条线。

以后 \(m\) 行，每行首先有两个数字 \((x,y)\)，代表了画线的起点坐标，接着用空格隔开一个字符，假如字符是 D，则是向下连一条边，如果是 R 就是向右连一条边。

输入数据不会有重复的边且保证正确。

注：纵向为\(x\)轴，例如1 1 D 的终点坐标为\((2,1)\)而不是\((1,2)\)

输出格式

输出一行：在第几步的时候结束。

假如 \(m\) 步之后也没有结束，则输出一行draw。

数据范围

\(1≤n≤200\)，
\(1≤m≤24000\)

题解

我们可以考虑当某些线段连接成环的最后一步是怎样的，我们从一个环上扯下一段，我们发现，如果在连接点 \(A\) 和 \(B\) 时形成了环，那么，\(A\) 和 \(B\) 就一定被某些线段连接起来了，或者说，如果添加线段\(AB\)时形成了环，那么节点 \(A\) 和 \(B\) 就一定是连通的。

我们可以用两个点是否处于同一个集合来判断连通，于是，我们想到了使用并查集实现它。

这里点是用二维坐标\((x,y)\) 表示的，并且编号从 \(1\) 开始，如果要将其转化为一维编号，那么，我们将其转化为从\(0\) 开始编号的坐标，于是：

\[d = n\times x+y \]

题解代码

#include<iostream>
using namespace std;
const int N = 210;

int s[N*N+N];
int n,m;

int decode(int x, int y){
    return x*n+y;
}

int root(int x){
    if(x!=s[x])s[x] = root(s[x]);
    return s[x];
}

int main(){
    scanf("%d%d",&n,&m);
    for(int i = 0;i<=n*n;i++)s[i] = i;

    for(int i = 0;i<m;i++){
        int x,y,nx,ny;
        char vec;
        scanf("%d%d %c",&x,&y,&vec);
        getchar();
        nx = x,ny = y;
        nx += (vec=='R');
        ny += (vec=='D');
        
        //计算起始和终点编号
        int a = decode(x-1,y-1),b = decode(nx-1,ny-1);
        
        //a b 早已连通，该步成环
        if(root(a)==root(b)){
            printf("%d\n", i+1);
            return 0;
        }else s[root(b)] = root(a);
    }    
    puts("draw");
    return 0;
}