《数据结构》学习笔记 第8章 高级搜索树 (Splay,RB,B-Tree)
1, Splay Tree
Splay Tree 定义:在一颗BBST中,某节点被访问,则随后将其移送至根节点。
- 数据局部性
逐层伸展 vs.双层伸展
- 精髓在于双层伸展(可减弱最坏情况的影响)
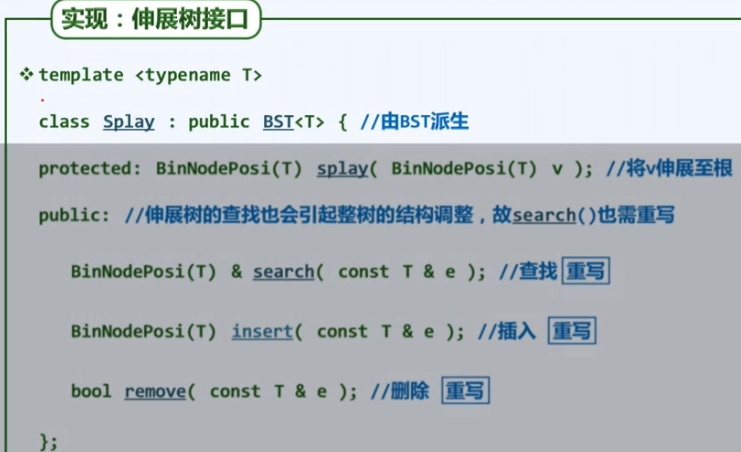
算法实现:
![]()
-
重点包含了Splay,search,insert,remove四种操作。
- Splay算法
- 四种情况,使用3+4统一算法;
- Search算法:不再属于静态操作,调用了Splay算法。
- 返回命中节点,或者(未命中)邻近节点。
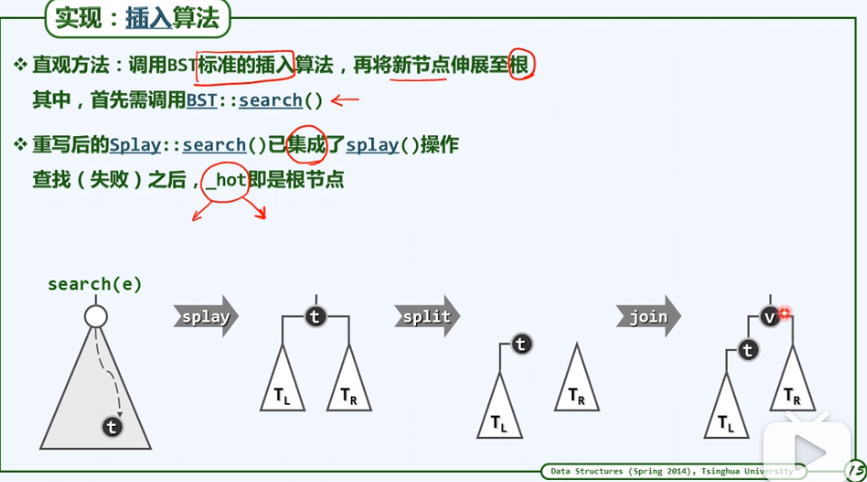
- Insert算法
-
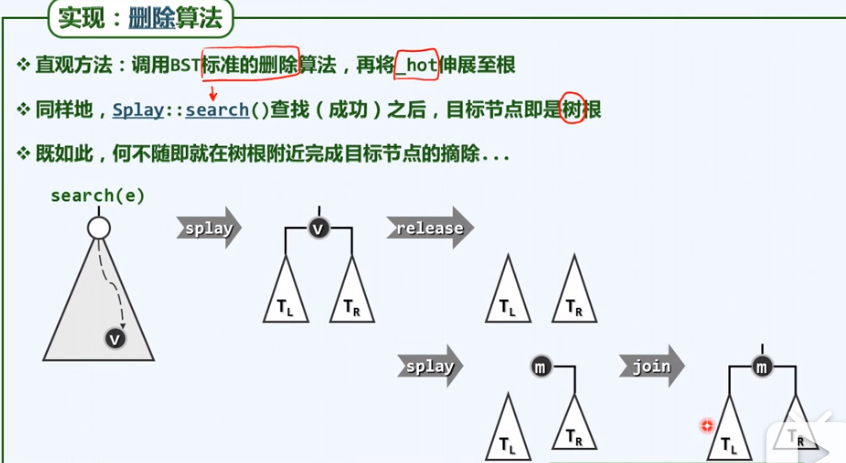
Remove算法
-
-
综合评价:
-
![]()
-
典型应用:电脑操作系统。
-
2,B-Tree
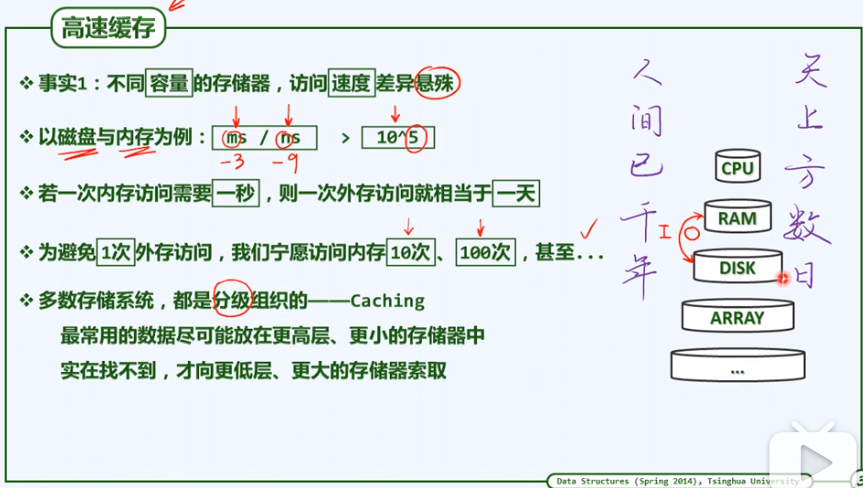
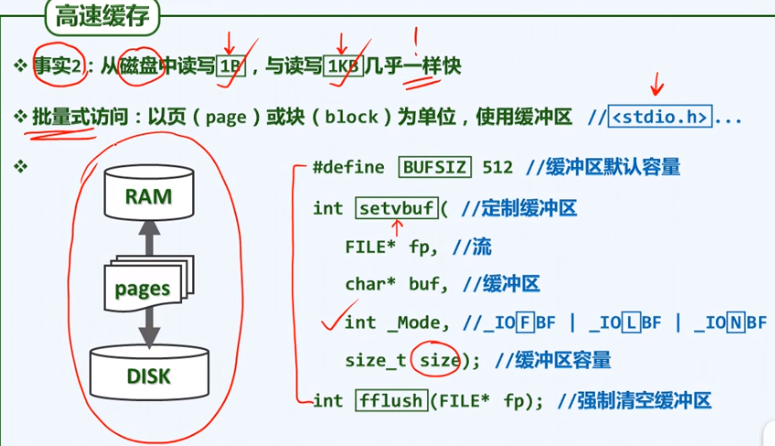
- 多路查找树,功能上等效于BST;目的:弥补不同存储级别之间巨大的访问速度差异;
- 存储器容量与访问速度的矛盾;解决方法;分级存储。
-
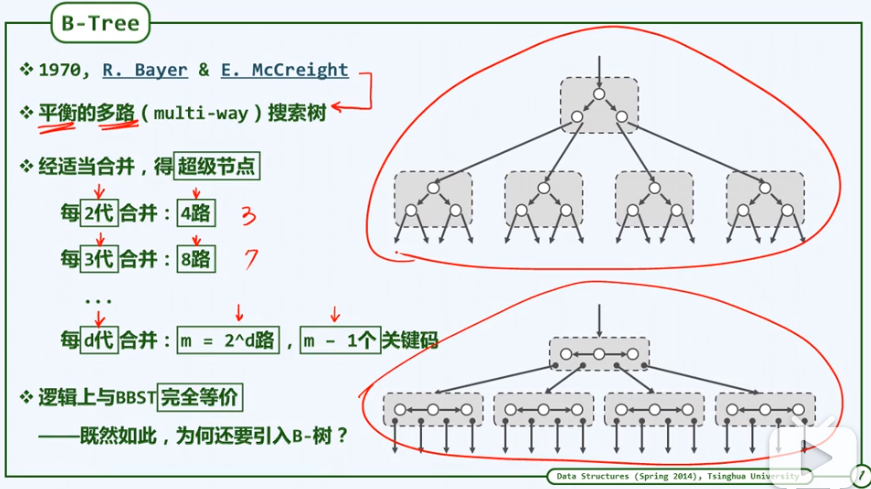
B树设计思路及定义:
-
![]()
-
![]()
-
定义需注意:外部节点与叶节点区别,深度统一,阶次含义,及其紧凑表示。
- 约束: 内部节点的分支数(n+1)不能太少:树根,n+1 >= 2; 其余n+1 >= Γm/2|.
- (2,4)B树与红黑树渊源很深。
-
-
B树的实现:
-
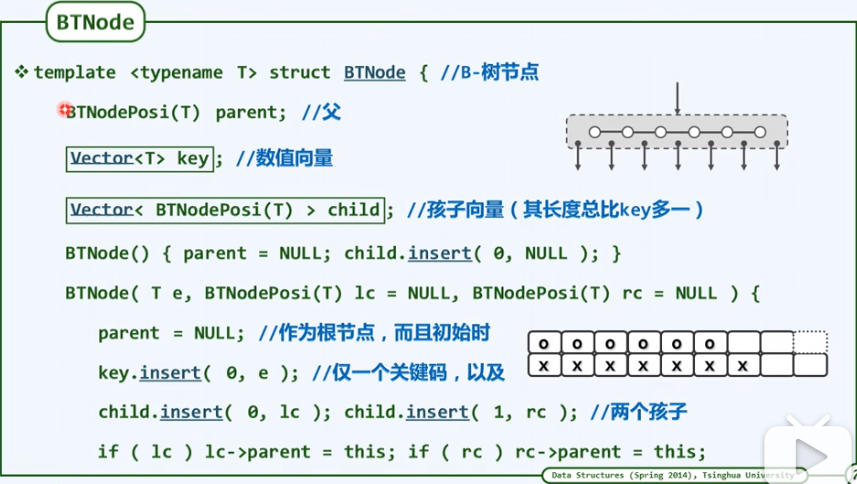
BTNode及BTree
-
-
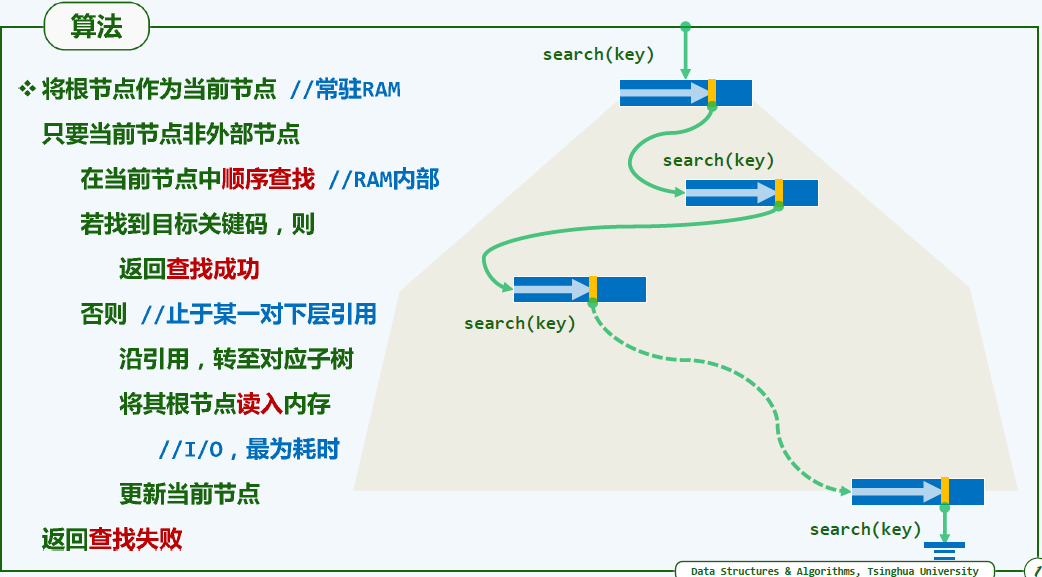
查找算法
![]()
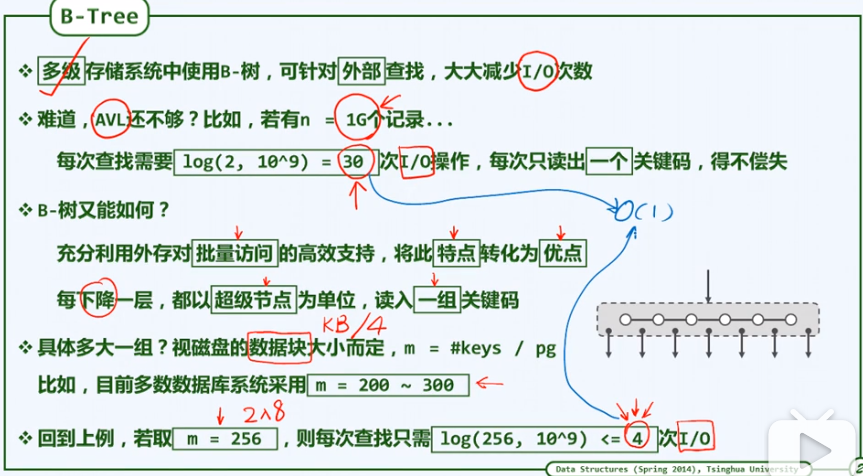
- 性能分析(复杂度):取决于两方面
- 1)节点载入内存,和 2)节点内的查找。
- 鉴于内存,外存速度的巨大差异,后者可忽略。前者次数直接取决于树高。
- 为了与I/O操作的延迟相匹配,每个节点大小设计为与I/O兑换的页面的大小相匹配。
- 大小通常为KB,几百个。
- 树高:最大:log[m]N,若m=256,则为BST高度的1/7. 最小:logmN,若m=256,则为BST高度的1/8.
- 1)节点载入内存,和 2)节点内的查找。
- 插入算法
- 先查找,后插入.如果发生上溢,则分裂:中位数节点移动到上一层。
- 上溢:因为新关键码的引入,导致分支总数超过了B树的阶次m。处理方法:分裂最多直至到根。
-
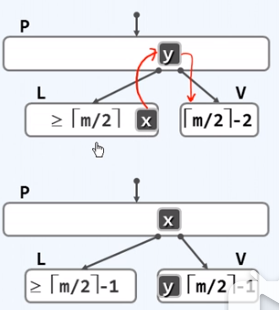
删除算法
- 下查找,找到后删除;若发生下溢,则旋转或者合并解决。
- 旋转:
![]() 合并最多直至到根;
合并最多直至到根;![]()
- 下溢:因为节点的删除,不满足B树关于节点/分支下限的规定。
-
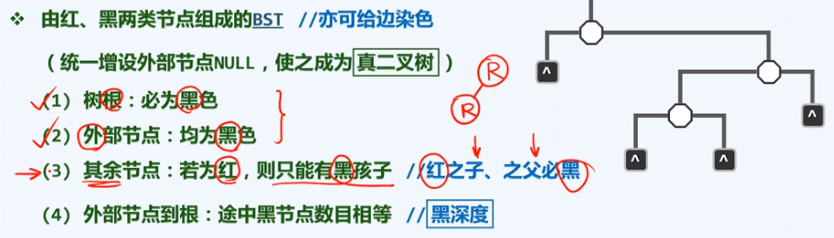
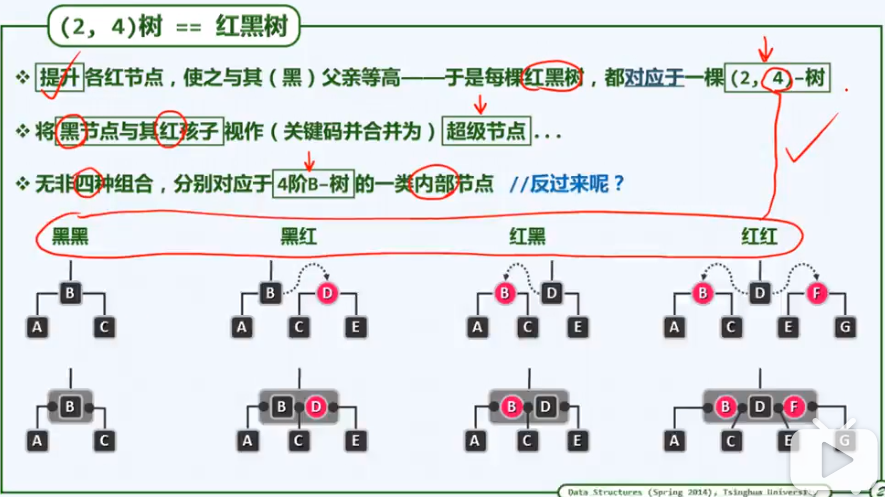
3, Red-Black Tree
- 一致性结构
- 红黑树规则定义:
![]()
-
规则的理解:提升变换(红色提升至跟其黑父亲同级),即等效转化为(2,4)树。
-
RB Tree接口定义:
-
-
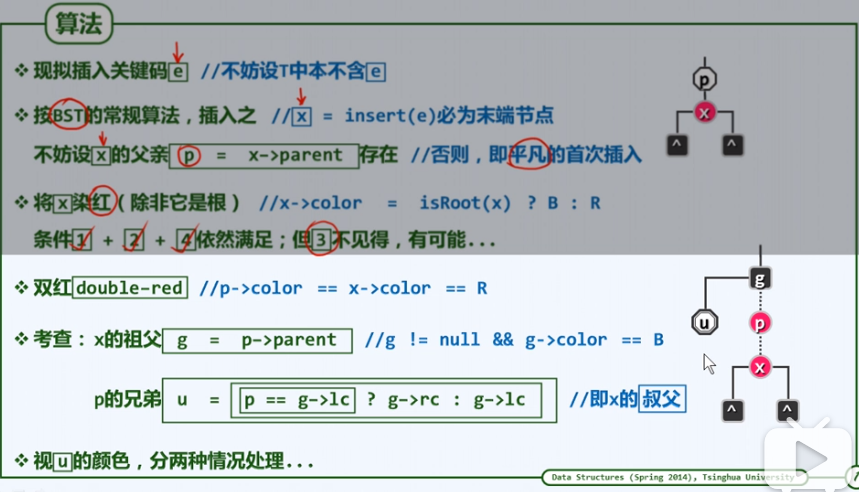
插入算法:
-
以曲为直:参照B树取理解RB Tree的变换。
-
算法定义:
![]()
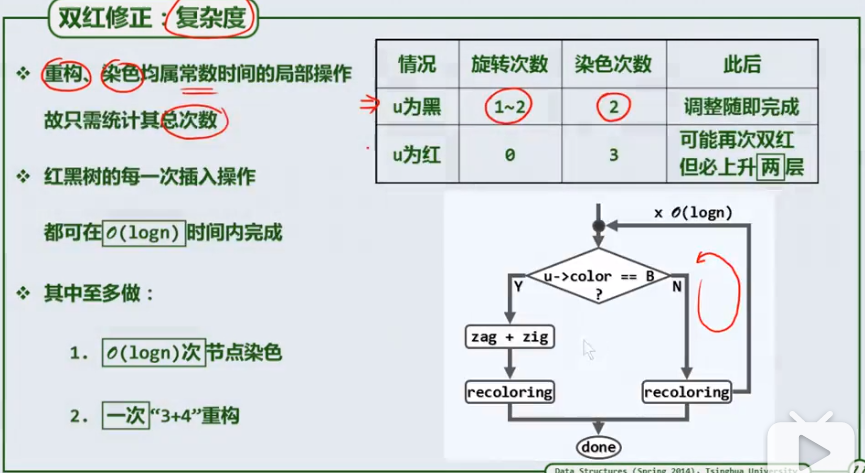
- 双红缺陷分两种情况:
- 叔父节点为黑;较好处理,换节点换颜色及或3+4重构即可。
- 叔父节点为红:换颜色即可。
-
![]()
-
-
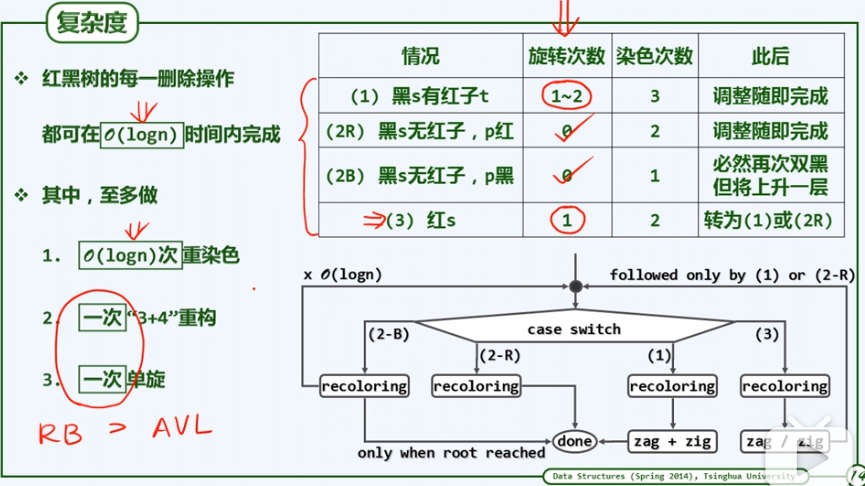
删除算法(相较于插入,情况更多):
-
x被删除后,由孩子r接替:
-
其中之一为红:很好处理,替代者r置为黑色。
-
两者都为黑(双黑缺陷, 黑高度则发生变化):
-
双黑缺陷,等效为修复B树的下溢缺陷。分四种情况:
-
![]()
-
-
-
归纳:
![]()
-



 合并最多直至到根;
合并最多直至到根;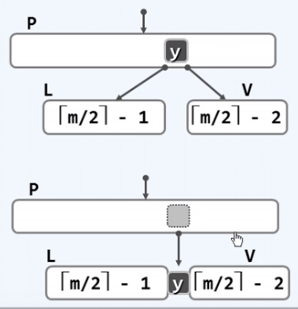



 浙公网安备 33010602011771号
浙公网安备 33010602011771号