【强连通分量】洛谷P2341 [USACO03FALL / HAOI2006] 受欢迎的牛 G_题解

原题链接

大致思路

可以将一些互相爱慕的奶牛视为一个家庭(强连通分量),那么这样我们就可以得到好几个家庭,这些家庭之间是不可能互相喜欢的.

如图:

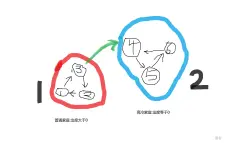
如果只一个家庭的出度为0,那么它肯定是一个高冷家庭最受欢迎的家庭,又因为一个家庭里的奶牛都是乱伦互相爱慕的,所以这个家庭中的奶牛都是受欢迎的.

但是这时候肯定有小盆友想问:"如果有好几个高冷家庭,会怎样呢?",没事,我们接着分析.

如图:

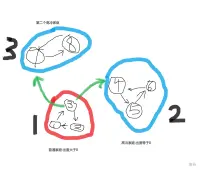
如果有好几个家庭的出度为0,那么任何一个高冷家庭都无法的得到所的家庭的爱,就没有最受欢迎的家庭了.

算法步骤

1.构建图：首先，根据输入构建一个有向图。
2.构建反向图：然后，构建这个图的反向图。
3.计算反向图的强连通分量：使用Tarjan算法计算反向图的强连通分量。
4.统计受欢迎的牛：对于每个强连通分量，检查是否有牛在原始图中没有出边（即没有认为其他牛受欢迎）。这样的牛就是被所有牛认为受欢迎的。

详细内容请看代码注释

代码

我知道你们最感兴趣的是什么

#include<bits/stdc++.h>
using namespace std;

const int N = 10010, M = 50010;//节点和边的数量上限

int n, m;
int head[N], k;
int dfn[N], low[N];//深度优先搜索编号和最低点编号
int t, ans, du[N];
bool instack[N];//标记节点是否在栈中
int member[N], id[N];//每个强连通分量的成员数和标识符
stack<int>s;//人见人爱,花见花开的栈
struct Edge{
	int to, next;
}edge[M * 2];
struct bian{
	int u, v;
}e[M];

void add(int u, int v){
	edge[++k].to = v;
	edge[k].next = head[u];
	head[u] = k;
}

void tarjan(int u){//Tarjan算法的核心函数，用于找出所有强连通分量(家庭)
	low[u] = dfn[u] = ++t;//将u节点的深度优先搜索编号最低点编号设置为当前时间t
	
	instack[u] = 1;//将u节点标记为在栈中
	s.push(u);//将u节点压入栈
	
	for(int i = head[u]; i; i = edge[i].next){//遍历u节点的所有邻接节点
		int v = edge[i].to;
		if(!dfn[v]){//如果v节点是干净的
			tarjan(v);
			low[u] = min(low[u],low[v]);//更新u节点的最低点编号
		}
		else if(instack[v]){
			low[u] = min(low[u],low[v]);//如果v节点在栈中,也更新u节点的最低点编号
		}
	}
	if(low[u] == dfn[u]){//如果u节点的最低点编号等于它的深度优先搜索编号,说明找到一个family~
		++ans;//家庭的数量增加
		//是的,没错你找到了!
		
		member[ans] = 0;//此强连通分量的成员数先初始化为(没有孩子)
		//去福利院认养
		while(s.top()!=u){//弹出栈中所有属于当前强连通分量的节点
			id[s.top()] = ans;//将节点的强连通分量标识符设置为当前分量的编号(给孩子一个领养证书)
			instack[s.top()] = 0;//将节点标记为不在栈中(有父母了,就可以从福利院中滚出去了)
			++member[ans];//更新当前强连通分量的成员数(孩子+1)
			s.pop();//弹出节点
		}
		id[s.top()] = ans;//将栈顶节点的标识符设置为此家庭的编号
		instack[s.top()] = 0;//将栈顶节点标记为不在栈中
		member[ans]++;//更新此家庭的成员数
		s.pop();//弹出栈顶节点
	}
}

int main(){
	cin >> n >> m;
	for(int i = 1; i <= m; ++i){
		int x, y;
		cin >> x >> y;
		e[i].u = x;
		e[i].v = y;
		add(y, x);//构建反向图
	}
	
	//组建家庭
	for(int i = 1; i <= n; ++i){//对每个节点调用tarjan函数
		if(!dfn[i]){//如果节点没有被访问过
			tarjan(i);
		}
	}
	
	for(int i = 1; i <= m; ++i){//遍历所有边
		if(id[e[i].u] != id[e[i].v]){//如果边的两个端点属于不同的家庭(不是一家人)
			++du[id[e[i].u]];//增加边的一个端点所在家庭的计数
		}
	}
	
	int temp = 0;
	for(int i = 1; i <= ans; ++i){ // 遍历所有强连通分量
		if(du[i] == 0){//此家庭的出度为0
			if(temp == 0){//如果之前没有找到出度为0的家庭
				temp = i;//高冷家庭!!!
			}
			else{//如果已经找到过一个出度为0的家庭
				cout << "0" << endl;//无法的得到所有家庭的爱,好伤心~
				return 0;
			}
		}
	}
	cout << member[temp] << endl; // 输出出度为0的家庭的成员数(这是什么乱伦家庭?)
	
	return 0;//我的任务,完成了!
}

小结

AC固然重要,但理解更是重中之重.