序列自动机详解
前言
今天花了一整天研究了大佬口中的“普及-”难度的序列自动机,感觉难度远不止普及……
其实,我翻遍了全网,一直没有找到详细讲解序列自动机这一知识点的文章(难道大佬们都懒得用这个最简单的自动机嘛
于是,为了水博客,这篇序列自动机的详解诞生了。
本文的所有代码均使用 C++ 语言。
前置芝士
- 图论
- DFS
- 好像没了
自动机的概念
首先,在讲解序列自动机这个玩意之前,我们先来看看什么是自动机。
自动机,指将一个字符串构造成一个有向无环图(DAG)的过程。我们约定下列名词[1]:
字母表
字母表是符号的有穷非空集合。我们规定,使用 \(\sum\) 表示字母表。常见的字母表有:
- \(\sum=\{a,b,\cdots,z\}\) :小写字母集合
- \(\sum=\{0,1,2,\cdots,10\}\) :十进制字母表
- \(\sum=\{0,1\}\) :二进制字母表
串
串(或单词)是从某个字母表中选定有穷个符号组成的序列。对于串,我们有以下约定:
- 空串:空串是出现 \(0\) 次符号的串,记作 \(\varepsilon\) 。任意字母表当中都可以有空串。
- 串的长度:我们在本文中约定,假设有串 \(a\) ,则 \(a\) 的长度记作 \(|a|\) 。串的长度即为串中字符的数量。
- 字母表的幂:如果 \(\sum\) 是一个字母表,那么我们可以使用指数符号表示该字母表某个长度所有串的集合。特别地,字母表 \(\sum\) 上的所有串的集合记作 \(\sum^*\),例如 \(\{0,1\}^*=\{\varepsilon,0,1,00,01,10,11,000,\cdots\}\) 。
- 排除空串:我们将字母表 \(\sum\) 上的所有非空串的集合记作 \(\sum^+\) 。
语言
\(\sum\) 是某个具体的字母表,则全部从 \(\sum^*\) 集合中选定的串的集合称为语言。
一般地,普通的语言可以看作若干串的集合。
了解了自动机的相关名词后,我们将讲解序列自动机的作用。
序列自动机
作用
序列自动机是一个可以快速判断任意字符串 \(t\) 是否包含子串 \(s\) 的算法。[2]
从本质上来讲,序列自动机虽然属于“自动机”的范畴,但并不与类似AC自动机、后缀自动机等高级算法一样需要高难度的知识。它仅仅是一个使用空间复杂度来提升时间复杂度的朴素算法。
原理
假定我们有一个串 \(s\) ,和数组 \(nxt\)。其中,\(nxt_{i,j}\) 表示在串 \(s\) 中,从第 \(i\) 个位置后的字母表中第 \(j\) 个元素首次出现的位置。
构造
很显然,对于 \(nxt\) 数组,我们需要对它进行构建。
我们可以从末尾往前依次计算当前出现的位置。对于每次遍历,\(nxt_{i,j}\) 初始等于 \(nxt_{i+1,j}\) 。
我们进行二重遍历:外层遍历当前位置,内层遍历当前元素。
伪代码如下。
For i n - 1 To 0 By -1
For j 0 To M By 1
nxt[i][j] ← nxt[i + 1][j]
End
nxt[i][s[i + 1] - 'a' + 1] ← i + 1
End
查找
我们可以对序列进行查找子串操作。
我们定义指针 \(p=-1\) ,对于每次循环,指针 \(p\) 都跳转到 \(nxt_{p+1,j}\) 的位置。如果当前 \(p\) 所指向的值为空,则说明母串中不存在子串的这个字符。
伪代码如下。
Integer p ← -1, l ← |t|
For i 0 To l By 1
p = nxt[p + 1][t[i] - 'a']
If p = NPOS
Then Return False
Else Continue
End
例题
既然学完了基本概念,那么我们来看一道例题,来把知识应用到实战中吧。
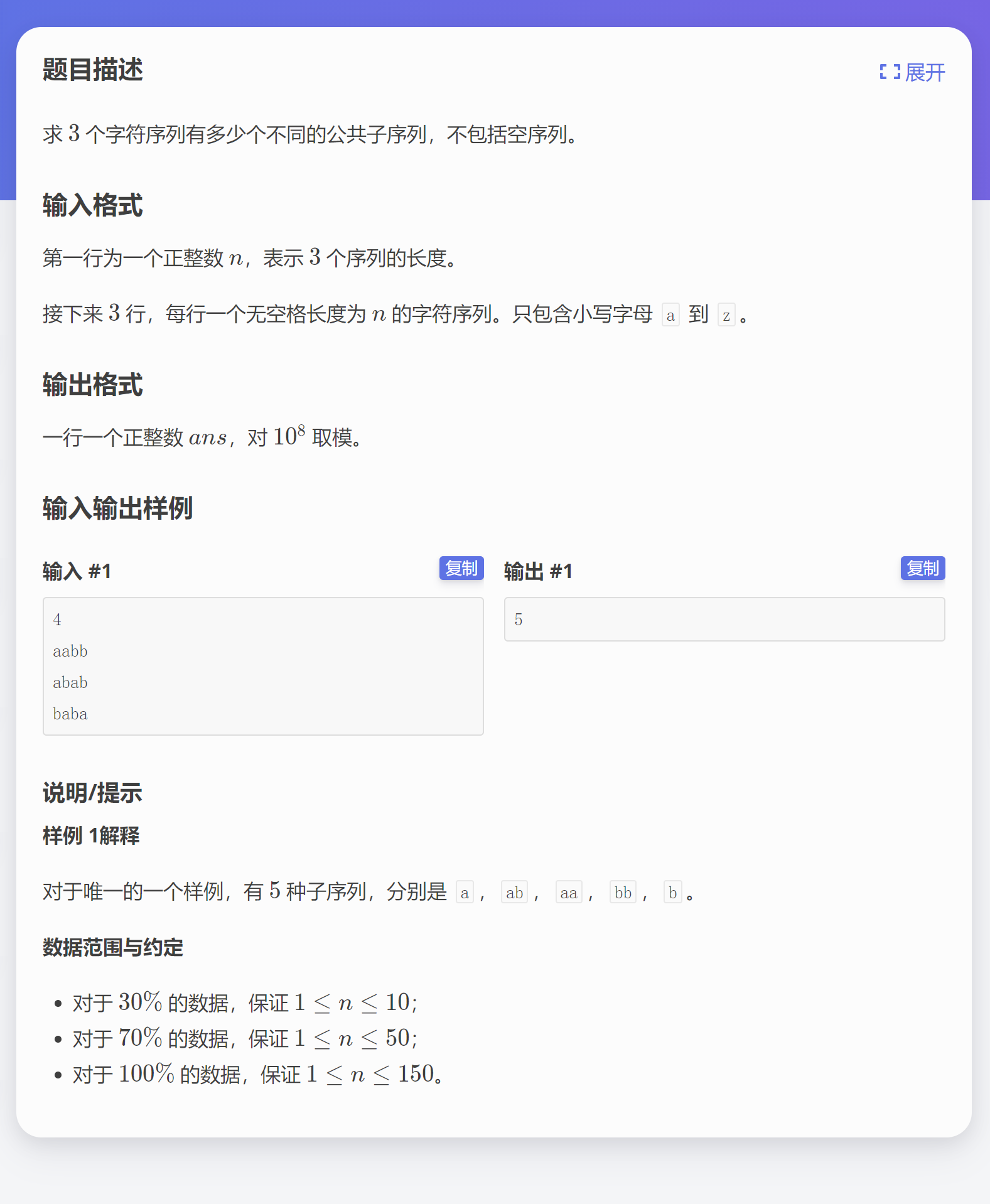
题目链接:洛谷P1819。
题意简述
给定 \(3\) 个长度为 \(n\) 的串,求这些串的公共非空子序列数量。
字符集 \(\sum = \{a,b,\cdots,z\}\) 。
分析
这其实是一道序列自动机的模板题。与我们上面所讲的不同的是,我们需要求多个不同串的公共子序列。
显然,我们可以对这三个串进行 DFS。为了提高效率,避免重复计算,我在此处选用了记忆化搜索进行优化。
我们不妨假设 \(dp\) 数组存储的是每一步的计算结果(记忆化数组)。其中,\(dp_{x,y,z}\) 代表我们的三个串分别从 \(x,y,z\) 开始的相同子序列个数。对于每次递归,我们都可以去枚举字母表中的每个字母。如果三个字符串都含有当前字母,那么就代表当前的公共子序列长度又增加了,我们可以进行进一步的搜索。
最后,只要当前的 \(x,y,z\) 不全等于 \(0\) ,我们就将 \(dp_{x,y,z}\) 加一。
参考代码
#include <iostream>
#include <cstdio>
#include <string>
#include <memory.h>
using namespace std;
const int MOD = 1e8, N = 160, MAXM = 30, M = 26, NPOS = 0x3f; // NPOS为数组默认值,查找子串时有用,M为字母表长度
const char ST = 'a'; // 字母表起始字符
class SequenceAM { // 序列自动机 Sequence Auto Machine
public:
int nxt[160][30]; // 核心数组
string s; // 当前串
void init() { // 初始化序列自动机
// for (int i = 0; i < 26; i++) this -> nxt[s.size()][i] = NPOS; // 如果要查找子串,需要进行初始化
for (int i = this -> s.size() - 1; i >= 0; i--) { // 倒序初始化
for (int j = 0; j < M; j++) this -> nxt[i][j] = this -> nxt[i + 1][j]; // 默认等于前一个的值
this -> nxt[i][this -> s[i] - ST] = i + 1; // 更新数组
}
}
bool find(string t) { // 查找函数,此程序中不会使用
int p = -1, length = t.size(); // p 指针
for (int i = 0; i < length; i++) { // 循环每个字符
p = this -> nxt[p + 1][t[i] - 'a']; // 指针跳转
if (p == NPOS) return 0; // 如果当前值为空(或不存在),返回未找到
}
return 1; // 子串t存在
}
};
SequenceAM a, b, c; // 三个串
long long dp[N][N][N]; // 记忆化数组
int n; // 串长度
long long dfs(int x, int y, int z) { // 本题核心:深搜
if (dp[x][y][z]) return dp[x][y][z]; // 记忆化
for (int i = 0; i < M; i++) { // 枚举每个字符
if (a.nxt[x][i] && b.nxt[y][i] && c.nxt[z][i]) { // 如果同时存在于三个串中
dp[x][y][z] = (dp[x][y][z] + dfs(a.nxt[x][i], b.nxt[y][i], c.nxt[z][i])) % MOD; // 继续dfs,并加上它的返回值,记得取余
}
}
if (x || y || z) dp[x][y][z]++; // 不都为0则加一
return dp[x][y][z] % MOD;
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cin >> n;
cin >> a.s >> b.s >> c.s; // 输入串
a.init(); b.init(); c.init(); // 初始化
cout << dfs(0, 0, 0) << endl; // 进行dfs
return 0;
}
双倍经验
复杂度分析
在下文中,我们设 \(l\) 为串长度,\(|\sum|\) 为字符集长度,\(M\) 表示 DFS 递归最大深度。
初始化
初始化的时间复杂度为 \(\Theta(l\times|\sum|)\) 。在字符集长度过大的情况下,可以使用可持久化线段树进行优化。
空间复杂度为 \(\Theta(l\times|\sum|)\) 。
寻找子串
判断子串 \(t\) 是否在串中的时间复杂度为 \(\Theta(l)\) ,空间复杂度为 \(\Theta(1)\) 。
寻找多个子串的公共子序列个数
使用 DFS 的情况下,时间复杂度为 \(\Theta(|\sum|)\) ,空间复杂度为 \(\Theta(l^n + M)\) 。
后记
学完了序列自动机,感觉还是挺不容易的。学习嘛,就是一个查漏补缺的过程。愿大家在 CSP / NOIP的赛场上,展现出自己的实力!


 浙公网安备 33010602011771号
浙公网安备 33010602011771号