如何解决机器学习树集成模型的解释性问题
01 机器学习模型不可解释的原因
前些天在同行交流群里,有个话题一直在群里热烈地讨论,那就是 如何解释机器学习模型 ,因为在风控领域,一个模型如果不能得到很好的解释一般都不会被通过的,在银行里会特别的常见,所以大多数同行都是会用 LR 来建模。但是,机器学习的模型算法这么多,不用岂不是很浪费?而且有些算法还十分好用的,至少在效果上,如XGBoost、GBDT、Adaboost。
那么,有同学就会问了,为什么这些算法会没有解释性呢?其实是这样子的,刚刚所说的那些模型都是一些集成模型,都是由复杂的树结构去组成的模型,对于人类来说我们很难直观地去解释为什么这个客户就是烂,到底是什么特征导致他烂?
02 特征重要度方法盘点
其实像XGBoost之类的模型还算是有解释性的了,我们常常都会看到有人用信息增益、节点分裂数来衡量特征的重要度,但是这真的是合理的吗?
在解释是否合理前,有2个概念需要先给大家普及一下:
1)一致性
指的是一个模型的特征重要度,不会因为我们更改了某个特征,而改变其重要度。比如A模型的特征X1的重要度是10,那么如果我们在模型里给特征X2加些权重以增大其重要度,重新计算重要度后,特征X1的重要度仍是10。不一致性可能会导致具有重要度较大的特征比具有重要度较小的特征更不重要。
2)个体化
指的是重要度的计算是可以针对个体,而不需要整个数据集一起计算。
好了,有了上面的认识,下面就来盘点一下目前常见的特征重要度计算的方法:
1)Tree SHAP:即 shapley加法解释,基于博弈论和局部解释的统一思想,通过树集成和加法方法激活shap值用于特征归因。
2)Saabas:一种个性化启发式特征归因方法。
3)mean(| Tree SHAP |):基于个性化的启发式SHAP平均的全局属性方法。
4)Gain:即增益,由Breiman等人提出的一种全局的特征重要度计算方法,在XGBoost、scikit learn等包中都可以调用,它是给定特征在分裂中所带来的不纯度的减少值,经常会被用来做特征选择。
5)Split Count:即分裂次数统计,指的是给定特征被用于分裂的次数(因为越重要的越容易被引用,和论文引用差不多一个道理吧)。
6)Permutation:即排序置换,指的是随机排列某个特征,看下模型效果误差的变化,如果特征重要的话,模型误差会变化得特别大。
其中,属于个体化的仅有1-2,3-6均属于全局性统计,也就是说需要整个数据集进去计算的。
而对于一致性情况,我们有一个例子来证明:
有2个模型,Model A 和 Model B,其中A和B完全一致,但是我们在计算预测值的时候,强行给 Model B 的 特征 Cough 加上 10分。如下图所示(点击看大图):
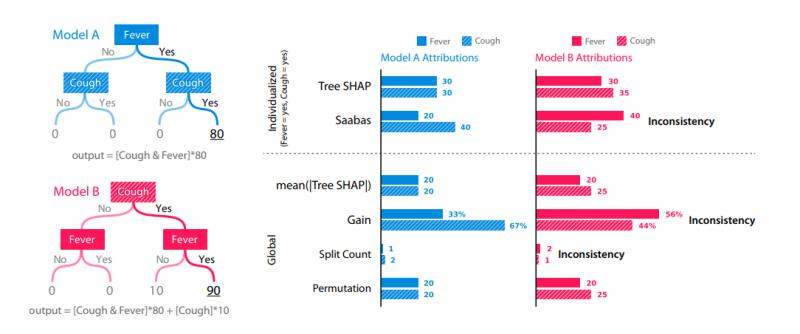
从实验结果可以看出以上6种方法的差别:
1)Saabas、Gain、Split Count均不满足 一致性 的要求,在改变了某个特征的权重之后,原先的特征重要度发生了改变,也直接导致重要度排序的改变。
2)而满足一致性要求的方法只有 Tree SHAP 和 Permutation了,而Permutation又是全局的方法,因此就只剩下了 Tree SHAP了。
03 SHAP可能是出路,SHAP到底是什么
SHAP(Shapley Additive exPlanation)是解释任何机器学习模型输出的统一方法。SHAP将博弈论与局部解释联系起来,根据期望表示唯一可能的一致和局部精确的加性特征归属方法。
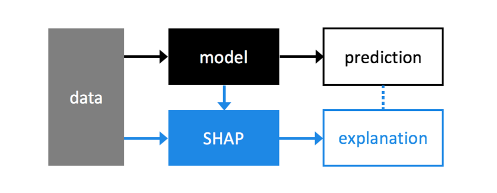
以上是官方的定义,乍一看不知所云,可能还是要结合论文(Consistent Individualized Feature Attribution for Tree Ensembles)来看了。
Definition 2.1. Additive feature attribution methods have an explanation model g that is a linear function of binary variables
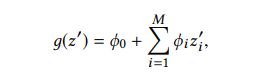
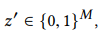
M是输入特征的个数, ϕi’ 就是特征的贡献度。ϕ0 是一个常数(指的是所有样本的预测均值)。SHAP 值有唯一的解,也具有3个特性:Local Accuracy、Missingness、Consistency。
1)Local Accuracy:即局部准确性,表示每个特征的重要度之和等于整个Function的重要度
2)Missingness:即缺失性,表示缺失值对于特征的重要度没有贡献。
3)Consistency:即一致性,表示改变模型不会对特征的重要度造成改变。
简单来说,SHAP值可能是唯一能够满足我们要求的方法,而我们上面讲到的XGBoost、GBDT等都是树模型,所以这里会用到 TREE SHAP。
04 SHAP的案例展示
0401 SHAP的安装
安装还是蛮简单的,可以通过终端的pip安装或者conda安装
pip install shap
or
conda install -c conda-forge shap
0402 对树集成模型进行解释性展示
目前TREE SHAP可以支持的树集成模型有XGBoost, LightGBM, CatBoost, and scikit-learn tree models,可以看看下面的demo:
import xgboost
import shap
# load JS visualization code to notebook
shap.initjs()
"""训练 XGBoost 模型,SHAP里提供了相关数据集"""
X,y = shap.datasets.boston()
model = xgboost.train({"learning_rate": 0.01}, xgboost.DMatrix(X, label=y), 100)
"""
通过SHAP值来解释预测值
(同样的方法也适用于 LightGBM, CatBoost, and scikit-learn models)
"""
explainer = shap.TreeExplainer(model)
shap_values = explainer.shap_values(X)
# 可视化解释性 (use matplotlib=True to avoid Javascript)
shap.force_plot(explainer.expected_value, shap_values[0,:], X.iloc[0,:])
output:
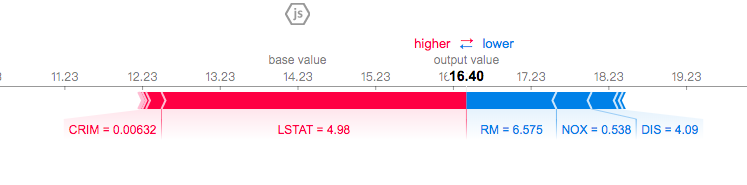
上面的图展示了每个特征的重要度,会预先计算好一个均值,将预测值变得更高的偏向于红色这边,反之蓝色。
这个数据集有这些特征:'CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT'
# visualize the training set predictions
shap.force_plot(explainer.expected_value, shap_values, X)
output:
上图可以看出每个特征之间的相互作用(输出图是可以交互的)。
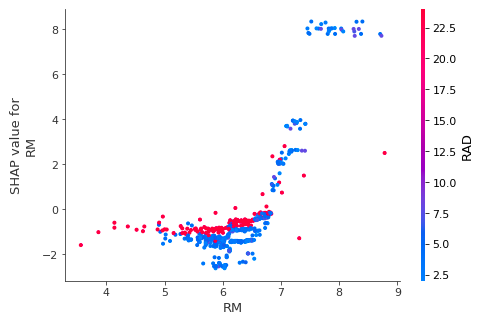
但是为了理解单个特性如何影响模型的输出,我们可以将该特性的SHAP值与数据集中所有示例的特性值进行比较。由于SHAP值代表了模型输出中的一个特性的变化,下面的图代表了预测的房价随着RM(一个区域中每栋房子的平均房间数)的变化而变化的情况。
单一RM值的垂直色散表示与其他特征的相互作用。要帮助揭示这些交互依赖关系,dependence_plot 自动选择 另一个特征来着色。比如使用RAD着色,突显了RM(每户平均房数)对RAD的值较高地区的房价影响较小。
"""创建一个SHAP图用于展示 单一特征在整个数据集的表现情况,每个点代表一个样本"""
shap.dependence_plot("RM", shap_values, X)
output:
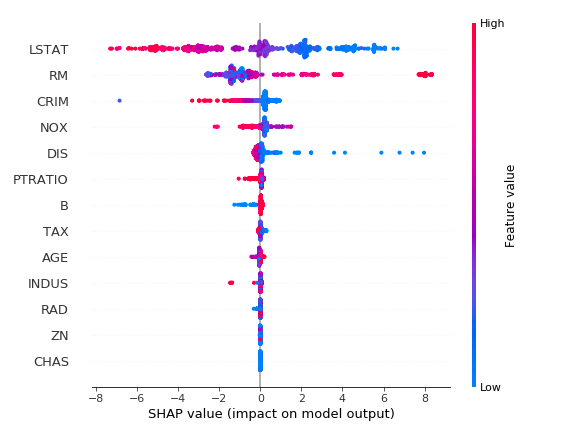
为了得到整体水平上每个特征的重要度情况,我们可以画出所有特征对于所有sample的SHAP值,然后根据SHAP值之和来降序排序,颜色代表特征重要度(红色代表高,蓝色代表低),每个点代表一个样本。
"""画出所有特征的重要度排序图"""
shap.summary_plot(shap_values, X)
output:
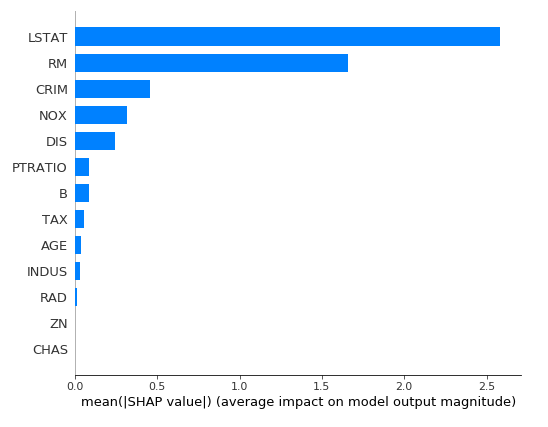
我们也可以只是显示SHAP值的所有样本的均值,画出bar图。
shap.summary_plot(shap_values, X, plot_type="bar")
output:
References
[1] A Unified Approach to Interpreting Model Predictions
http://papers.nips.cc/paper/7062-a-unified-approach-to-interpreting-model-predictions.pdf
[2] Consistent Individualized Feature Attribution for Tree Ensembles
https://arxiv.org/pdf/1802.03888.pdf
[3] Interpretable Machine Learning
https://christophm.github.io/interpretable-ml-book/
[4] shap 官方文档
https://github.com/slundberg/shap
本文由博客一文多发平台 OpenWrite 发布!


 浙公网安备 33010602011771号
浙公网安备 33010602011771号