2024牛客暑期多校训练营5 B题珑，E题安 ，H题入，L题知

题目：B题-珑

 

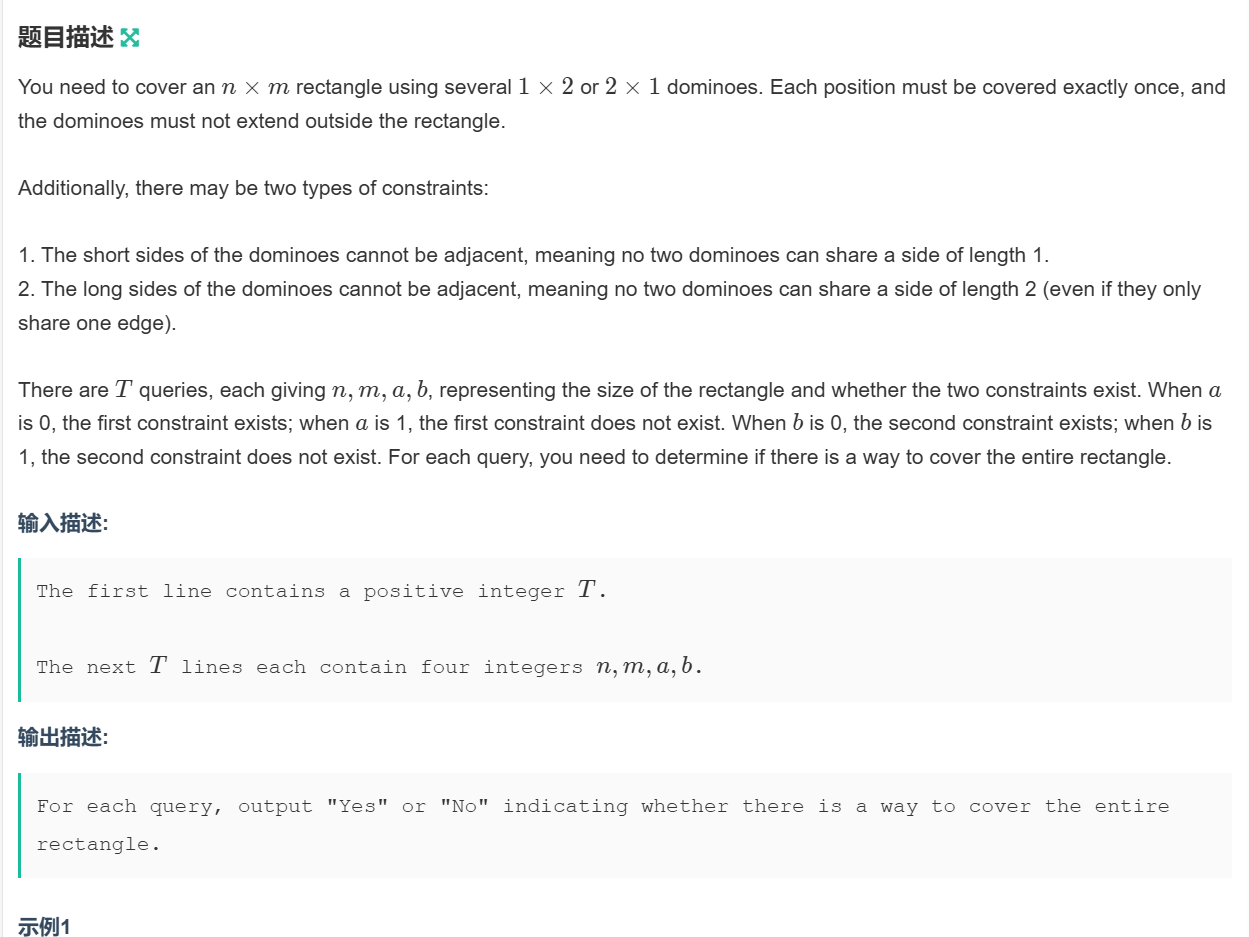
//示例1
5
3 3 1 1
2 4 0 1
1 5 1 0
5 5 0 0
1 2 0 0
//输出
No
Yes
No
No
Yes

 

 题解思路：

　　首先，（n x m）长方形格只能用（1x2）和（2x1）的多米诺骨牌来填充，多米诺骨牌的面积都是偶数，故面积为奇数的长方形是肯定填充不满的。接下来考虑（n x m）的面积的为偶数的情况：

• （a=1 and b=1）两种限制都没有自然，自然任意（n x m）为奇数的长方形都可以被填充满。
• （a=0 and b=0）两种限制都存在，即两个方块不能有长为1或者2的共边。这种情况只有n x m=2时才可以被填充满。
• （a=1 and b=0）只存在一种限制，既不能有长度为2的共边，只需要n=1 并且m是偶数或者m=1并且n是偶数的情况下，长方形可以被填满。

•  （a=0 and b=1）只存在一种限制，既不能有长度为1的共边，这种情况比较复杂。

                                                                                              

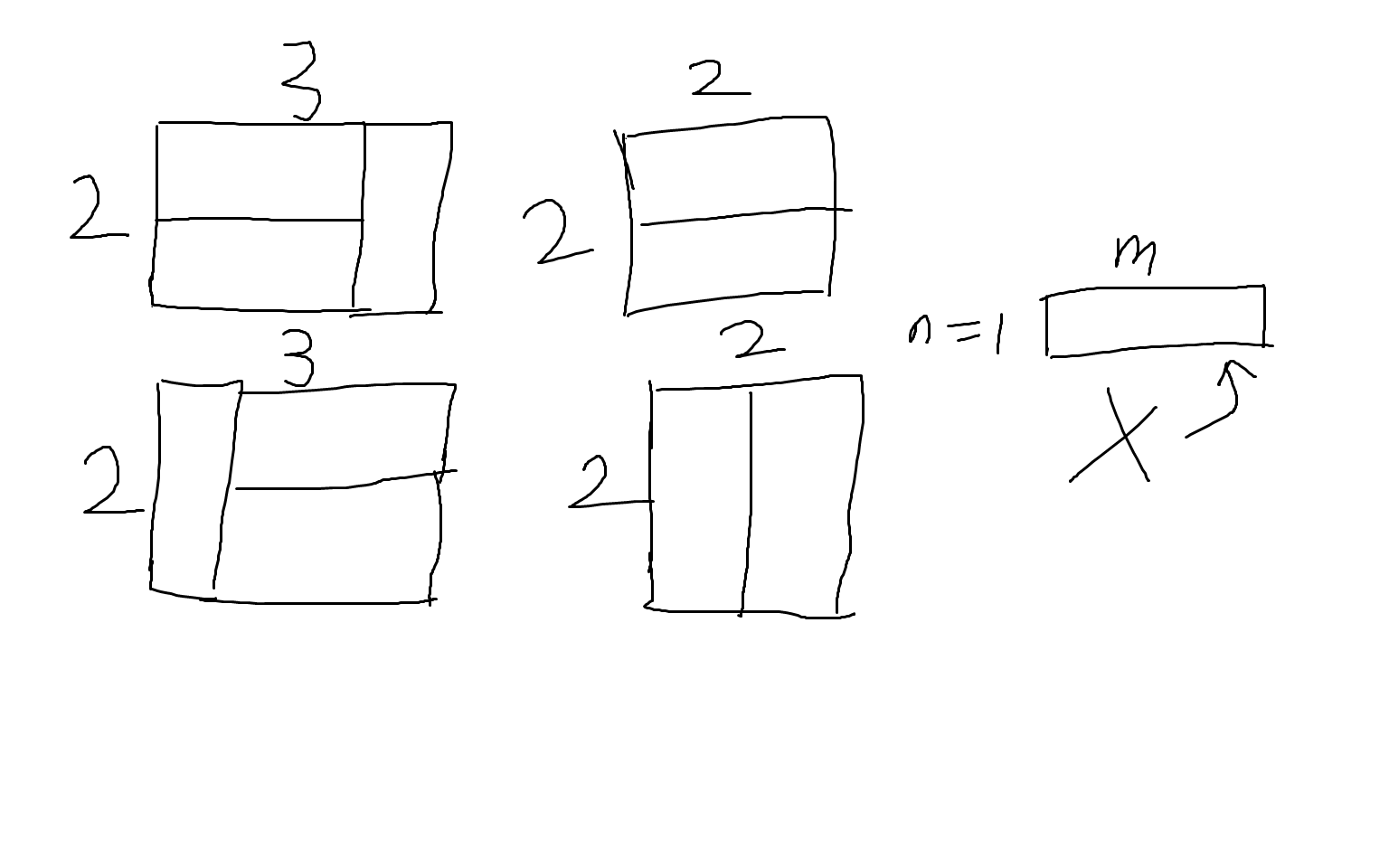
　　　　如图所示，我们将（1x2）多米诺骨牌组成如图所示的单元组，可以保证，当n!=1&& m!=1时，任意（nxm）的长方形可以由以上单元组组成。

 

代码编写：　　

#include<iostream>
#include<algorithm>
#include<vector>
#include<map>
#include<cmath>
#include<string>
#include<cstdlib>

using namespace std;
typedef long long ll;

void solve()
{
    ll n, m,a,b;
    cin >> n >> m >> a >> b;
    if((n*m)%2 == 1 )//n*m可能大于int类型改成long long类型
    {
        cout << "No\n";
    }
    else
    {
        if(a==1 && b==1)
        {
            cout<< "Yes\n";
        }
        else if(a==0 && b==0)
        {
            if(n*m==2)
            {
                cout << "Yes\n";
            }
            else cout<< "No\n";
        }
        else if(b==1)
        {
            if(n==1 || m==1)
            {
                if(n*m==2)cout << "Yes\n";
                else cout<< "No\n"; 
            }
            else if(n%2==0  || m%2==0 )
            {
                cout << "Yes\n";
            }
            else
            {
                cout << "No\n"; 
            }
        } 
        else if(a==1)
        {
            if(n==1 || m==1)cout << "Yes\n";
            else cout << "No\n";
        }
    }
}
signed main()
{
    int t;
    cin >> t;
    while(t--)
    solve();
    return 0;
}

题目：E-安

 

//示例1
输入
2
2
2 2
2 2
5
19 11 11 12 16
17 20 18 14 13
输出
1
2
备注：
1≤T≤2000,1≤n≤105,∑n≤105,1≤ai​,bi​≤109.

 

题解思路：　　

　　　首先，May和Ray各自有n个士兵相对站立，那么为了使各自的最后存活的骑士最多，他们各自要保证相对站立的骑士，生命值高的骑士必须要赢。因为May先手，所以May生命值高的骑士必定能赢。然后考虑生命值相等的士兵，因为May先手，所以这一轮比拼May肯定能赢。但是因为Ray生命值先归零，下一轮生命值相等的比拼中，May就成后手了。这样May与Ray相互交换先手。

代码编写：

#include<iostream>
#include<algorithm>
#include<vector>
#include<map>
#include<cmath>
#include<string>
#include<cstdlib>
using namespace std;
typedef long long ll;

void solve()
{
    int n;
    cin >> n ;
    ll lt=0,eq=0;
    vector<int> a(n),b(n);
    for(int i=0;i<n;i++)cin >> a[i];
    for(int i=0;i<n;i++)
    {
        cin >> b[i];
        if(a[i]>b[i])lt++;//统计生命值大于对方的回合；
        else if(a[i]==b[i])eq++;//统计生命值相等的回合；
    }
    cout << lt+(eq+1)/2 << endl;//生命值相等时May一赢一输。
}
signed main()
{
    int t;
    cin >> t;
    while(t--)
    solve();
    return 0;
}

 

题目：L-知

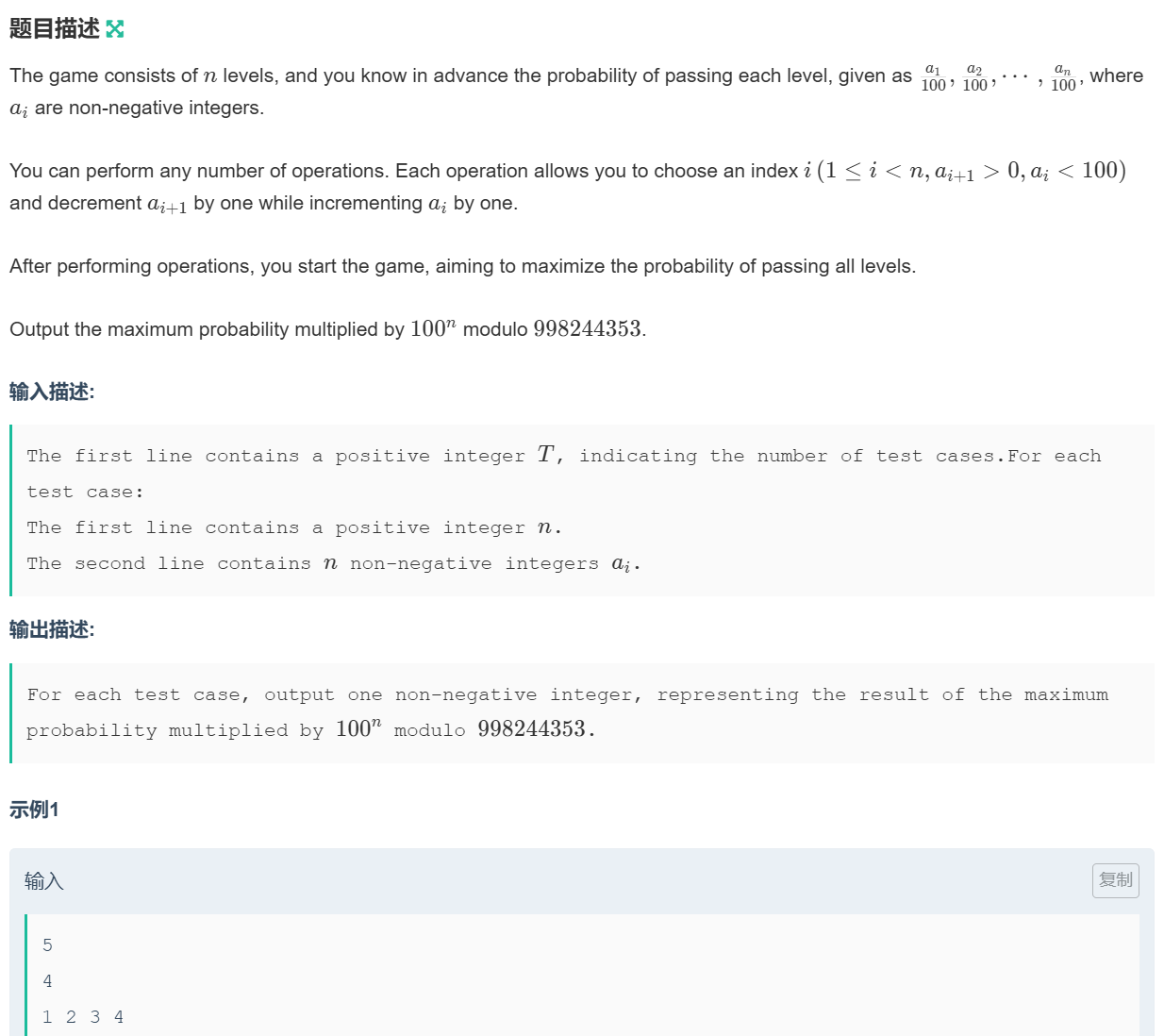
题意解读：每一个测试会给我们一串测试，里面包含n个数，每次操作会选定一个数a_i的值加1，同时a_i+1的值减1。这样的操作可以重复无数次，让你输出最后所有值相乘最大的情况。由题意可知，所有数相加的总和是不变的，因此，每个数的差值要尽可能的做到最小。因此，我的思路对每一个数进行遍历，如果现在这个数的值比下一个值要小，则要进行一次操作，并且回到前一个数。这样通过每一步骤操作，维护这种性质，就可以做到，每一个数的差值尽可能的小。注意进行取模。注意1≤T,n,ai​≤100.

 

 

#include<iostream>
#include<algorithm>
#include<string>
#include<cstdio>
#include<string>
#include<cstdlib>
#include<vector>
#include<map>
using namespace std;
typedef long long ll;
const int mod=998244353;
int a[105];
void solve()
{
    int n;cin >> n;
    for(int i=1;i<=n;i++)cin >> a[i];
    for(int i=1;i<n;)
    {
        if(a[i]<a[i+1])
        {
            a[i]++;
            a[i+1]--;
            if(i!=1)
            {
                i--;
             } 
             continue;
         } 
         i++;
    }
    ll ans=1;
    for(int i=1;i<=n;i++)
    {
        ans=(ans*a[i])%mod;
    }
    cout << ans << "\n";
}
signed main()
{
    int t;
    cin >> t;
    while(t--) 
    solve();
    return 0;
 }