机器学习之线性回归。

里面有不少过时了，然后有些数据在本地跑不动。正好AI兴起，就抄过来修改了一下。

这是个预测房价的，想着学下机器学习，应用到业务做下销量预测。

--------------------------------------------------------------------------------------------------

结果：

训练集模型评估指标：
均方误差（MSE）：48743825008.00
均方根误差（RMSE）：220780.04
平均绝对误差（MAE）：135488.22
决定系数（R²）：0.6495

背景：

原项目代码链接：https://github.com/NLP-LOVE/ML-NLP

从给定的房屋基本信息以及房屋销售信息等，建立一个回归模型预测房屋的销售价格。数据下载请点击：下载，密码：mfqy。

数据说明：数据主要包括2014年5月至2015年5月美国King County的房屋销售价格以及房屋的基本信息。数据分为训练数据和测试数据，分别保存在kc_train.csv和kc_test.csv两个文件中。其中训练数据主要包括10000条记录，14个字段，主要字段说明如下：第一列“销售日期”：2014年5月到2015年5月房屋出售时的日期第二列“销售价格”：房屋交易价格，单位为美元，是目标预测值第三列“卧室数”：房屋中的卧室数目第四列“浴室数”：房屋中的浴室数目第五列“房屋面积”：房屋里的生活面积第六列“停车面积”：停车坪的面积第七列“楼层数”：房屋的楼层数第八列“房屋评分”：King County房屋评分系统对房屋的总体评分第九列“建筑面积”：除了地下室之外的房屋建筑面积第十列“地下室面积”：地下室的面积第十一列“建筑年份”：房屋建成的年份第十二列“修复年份”：房屋上次修复的年份第十三列"纬度"：房屋所在纬度第十四列“经度”：房屋所在经度

测试数据主要包括3000条记录，13个字段，跟训练数据的不同是测试数据并不包括房屋销售价格，学员需要通过由训练数据所建立的模型以及所给的测试数据，得出测试数据相应的房屋销售价格预测值。

　　步骤：

1.选择合适的模型，对模型的好坏进行评估和选择。
2.对缺失的值进行补齐操作，可以使用均值的方式补齐数据，使得准确度更高。
3.数据的取值一般跟属性有关系，但世界万物的属性是很多的，有些值小，但不代表不重要，所有为了提高预测的准确度，统一数据维度进行计算，方法有特征缩放和归一法等。
4.数据处理好之后就可以进行调用模型库进行训练了。
5.使用测试数据进行目标函数预测输出，观察结果是否符合预期。或者通过画出对比函数进行结果线条对比。

核心的：

特征缩放，归一化处理

# 初始化归一化工具（将特征值缩放到0~1范围，提升模型训练效率）
scaler = MinMaxScaler()

# 训练集：先用fit计算缩放参数（如最大值、最小值），再用transform转换
X_train_scaled = scaler.fit_transform(X_train)

# 测试集：直接用训练集的缩放参数转换（关键！避免数据泄露）
X_test_scaled = scaler.transform(X_test)

# 将缩放后的数组转回DataFrame（保留列名，方便后续查看和使用）
X_train_scaled = pd.DataFrame(X_train_scaled, columns=X_train.columns)
X_test_scaled = pd.DataFrame(X_test_scaled, columns=X_test.columns)

模型训练与评估

# 初始化线性回归模型
model = LinearRegression()

# 训练模型：用缩放后的训练特征和真实房价拟合模型
model.fit(X_train_scaled, y_train)

# 用训练好的模型预测训练集房价（用于评估模型在已知数据上的表现）
train_preds = model.predict(X_train_scaled)

运用模型输出:

# 用训练好的模型预测测试集房价（测试集无真实房价，用于最终输出）
test_preds = model.predict(X_test_scaled)

# 将预测结果转换为DataFrame并保存为CSV
result_df = pd.DataFrame(test_preds, columns=['预测房价'])  # 增加列名“预测房价”
result_df.to_csv(RESULT_PATH, index=False)  # index=False：不保存行索引（避免多余数据）

print(f"\n测试集预测结果已保存至：{RESULT_PATH}")

新修改完整代码：

from __future__ import print_function
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.preprocessing import MinMaxScaler
from sklearn.linear_model import LinearRegression
from sklearn.metrics import (mean_squared_error, mean_absolute_error,
                             r2_score)  # 增加更多评估指标

# --------------------------
# 基础配置
# --------------------------
plt.rcParams["font.family"] = ["SimHei"]
plt.rcParams['axes.unicode_minus'] = False
np.random.seed(36)

# 文件路径
TRAIN_PATH = r'D:\01\ML-NLP\Machine Learning\Liner Regression\demo\kc_train.csv'
TEST_PATH = r'D:\01\ML-NLP\Machine Learning\Liner Regression\demo\kc_test.csv'
RESULT_PATH = r'D:\01\ML-NLP\Machine Learning\Liner Regression\demo\result.csv'


# --------------------------
# 数据处理
# --------------------------
# 读取并分离特征与目标变量
train_data = pd.read_csv(TRAIN_PATH)
X_train = train_data.drop(train_data.columns[1], axis=1)  # 删除价格列（第2列）
y_train = train_data.iloc[:, 1]  # 价格列作为目标变量

# 读取测试数据并对齐特征列
X_test = pd.read_csv(TEST_PATH)
X_test.columns = X_train.columns  # 强制对齐列名

# 特征缩放
scaler = MinMaxScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)

# 转回DataFrame
X_train_scaled = pd.DataFrame(X_train_scaled, columns=X_train.columns)
X_test_scaled = pd.DataFrame(X_test_scaled, columns=X_test.columns)


# --------------------------
# 模型训练与多指标评估
# --------------------------
model = LinearRegression()
model.fit(X_train_scaled, y_train)

# 训练集预测
train_preds = model.predict(X_train_scaled)

# 计算多种评估指标
mse = mean_squared_error(y_train, train_preds)
rmse = np.sqrt(mse)  # 均方根误差（更直观，单位与目标变量一致）
mae = mean_absolute_error(y_train, train_preds)  # 平均绝对误差
r2 = r2_score(y_train, train_preds)  # 决定系数（越接近1越好）

# 打印评估指标
print("训练集模型评估指标：")
print(f"均方误差（MSE）：{mse:.2f}")
print(f"均方根误差（RMSE）：{rmse:.2f}")  # 反映误差的平均大小
print(f"平均绝对误差（MAE）：{mae:.2f}")  # 反映误差的平均绝对值
print(f"决定系数（R²）：{r2:.4f}")  # 反映模型解释数据的能力（1为完美）


# --------------------------
# 多图表可视化评估
# --------------------------
# 设置画布，创建多个子图
fig, axes = plt.subplots(2, 2, figsize=(16, 14))
fig.suptitle('模型评估可视化', fontsize=16)

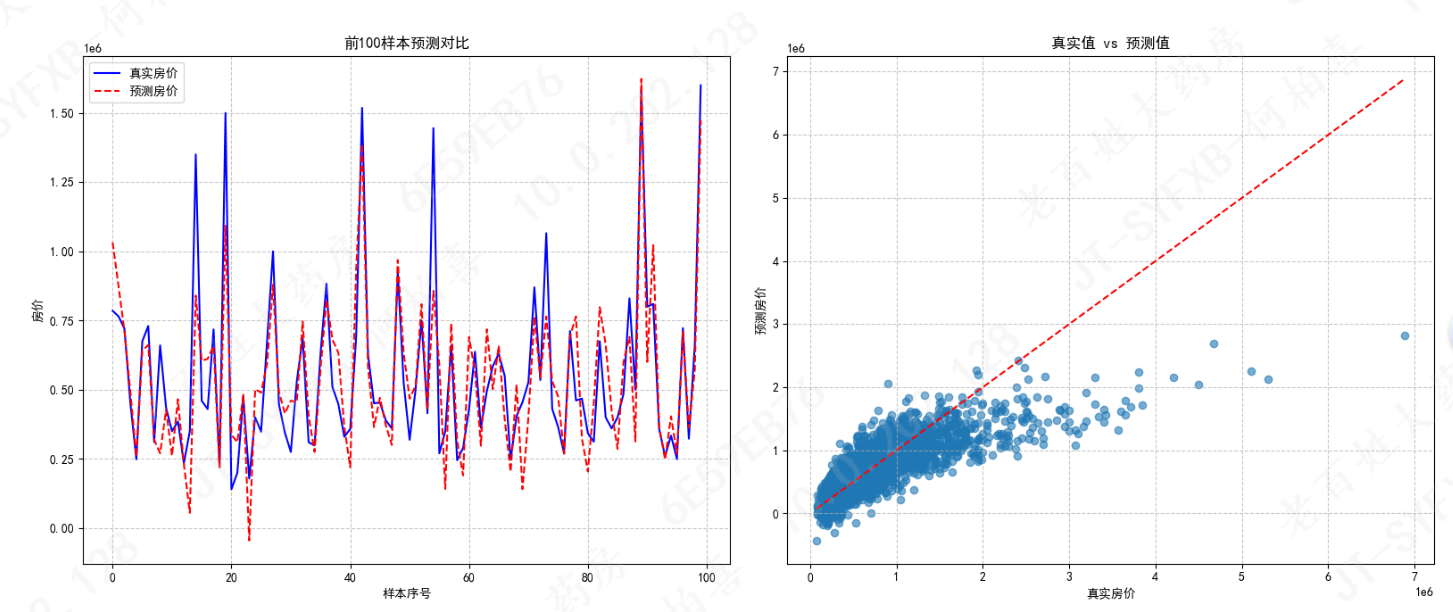
# 1. 真实值 vs 预测值（折线图）
axes[0, 0].plot(range(100), y_train[:100].values, label='真实房价', color='blue')
axes[0, 0].plot(range(100), train_preds[:100], label='预测房价', color='red', linestyle='--')
axes[0, 0].set_title('前100样本预测对比')
axes[0, 0].set_xlabel('样本序号')
axes[0, 0].set_ylabel('房价')
axes[0, 0].legend()
axes[0, 0].grid(linestyle='--', alpha=0.7)

# 2. 真实值 vs 预测值（散点图）
# 理想情况下应接近对角线，偏离越远说明预测越差
axes[0, 1].scatter(y_train, train_preds, alpha=0.6)
axes[0, 1].plot([y_train.min(), y_train.max()], 
                [y_train.min(), y_train.max()], 
                'r--')  # 对角线（完美预测线）
axes[0, 1].set_title('真实值 vs 预测值')
axes[0, 1].set_xlabel('真实房价')
axes[0, 1].set_ylabel('预测房价')
axes[0, 1].grid(linestyle='--', alpha=0.7)

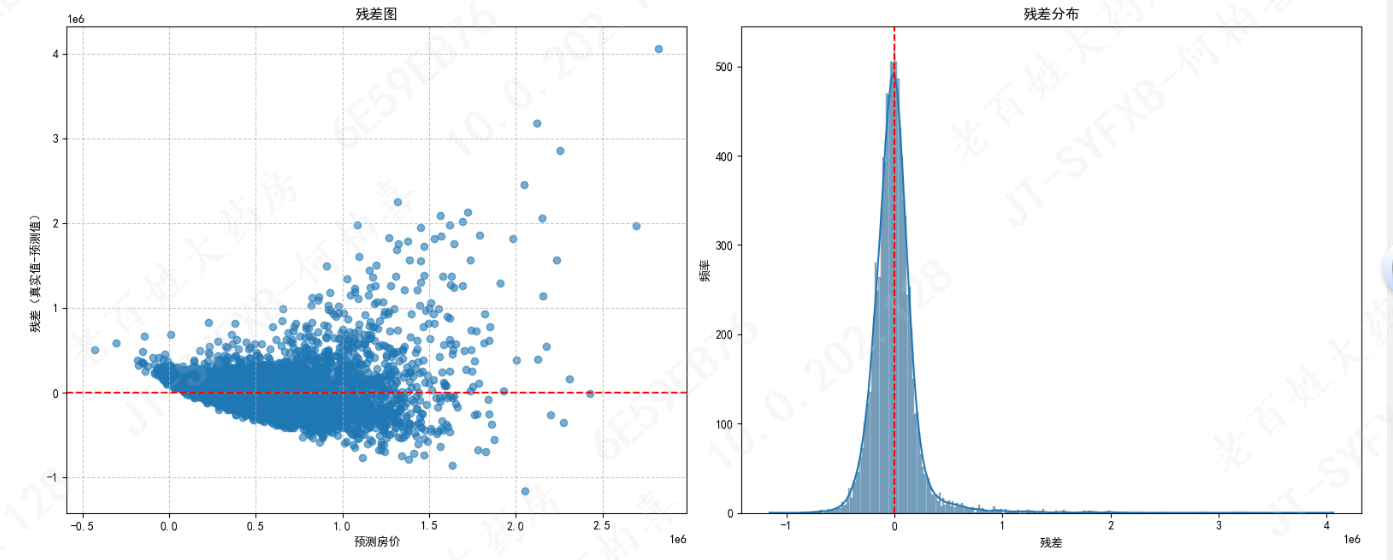
# 3. 残差图（预测误差分布）
residuals = y_train - train_preds  # 残差 = 真实值 - 预测值
axes[1, 0].scatter(train_preds, residuals, alpha=0.6)
axes[1, 0].axhline(y=0, color='r', linestyle='--')  # 残差为0的参考线
axes[1, 0].set_title('残差图')
axes[1, 0].set_xlabel('预测房价')
axes[1, 0].set_ylabel('残差（真实值-预测值）')
axes[1, 0].grid(linestyle='--', alpha=0.7)

# 4. 残差分布直方图（检查是否正态分布）
# 若残差近似正态分布，说明模型误差较随机，性能较好
sns.histplot(residuals, kde=True, ax=axes[1, 1])
axes[1, 1].axvline(x=0, color='r', linestyle='--')  # 残差为0的参考线
axes[1, 1].set_title('残差分布')
axes[1, 1].set_xlabel('残差')
axes[1, 1].set_ylabel('频率')

plt.tight_layout(rect=[0, 0, 1, 0.96])  # 调整布局，避免标题重叠
plt.show()


# --------------------------
# 测试集预测与保存
# --------------------------
test_preds = model.predict(X_test_scaled)
result_df = pd.DataFrame(test_preds, columns=['预测房价'])
result_df.to_csv(RESULT_PATH, index=False)
print(f"\n测试集预测结果已保存至：{RESULT_PATH}")

posted @ 2025-08-08 16:13 Sakura_柏阅读(8) 评论(0) 收藏举报

刷新页面返回顶部

Sakura_柏

十年如一梦，依旧五云高欢迎联系交流wx：baixi425

机器学习之线性回归。

公告

Sakura_柏

十年如一梦，依旧五云高 欢迎联系交流wx：baixi425

机器学习之线性回归。

公告

十年如一梦，依旧五云高欢迎联系交流wx：baixi425