排序算法

a. 排序算法的基本思想

b. 排序算法的过程 

c. 排序算法的性能（时间复杂度、空间复杂度、稳定性） 

稳定性：保证排序前后两个相等的数的相对顺序不变。 
依次比较的是稳定的，跳跃比较的是不稳定的（步子迈大了，容易扯着蛋，哈哈哈就是这个意思）。

插入类排序 

插入排序的基本思想是：在一个已排好序的记录子集的基础上，每一步把下一个待排序的记录有序地插入到已排好序的记录子集中，直到所有待排记录被全部插入为止。 
打扑克时的抓牌就是插入排序的一个典型情境，每抓一张牌，插入到合适位置，直到抓完牌为止，即可得到一个有序序列。

1. 直接插入排序

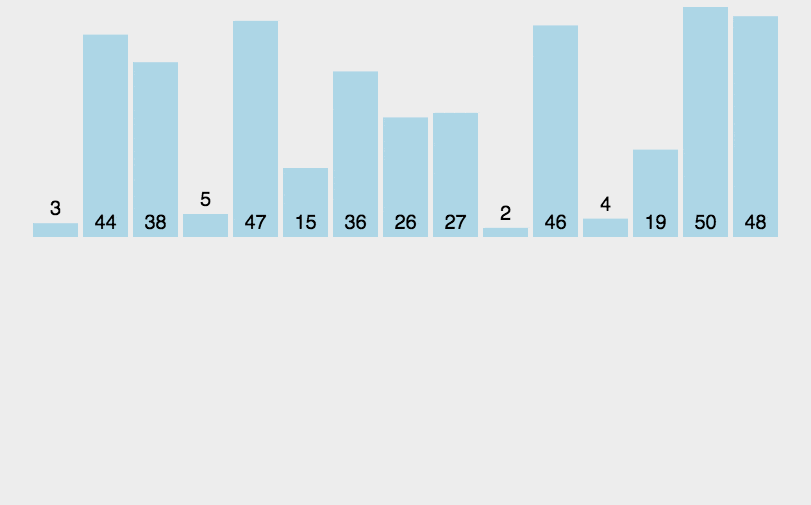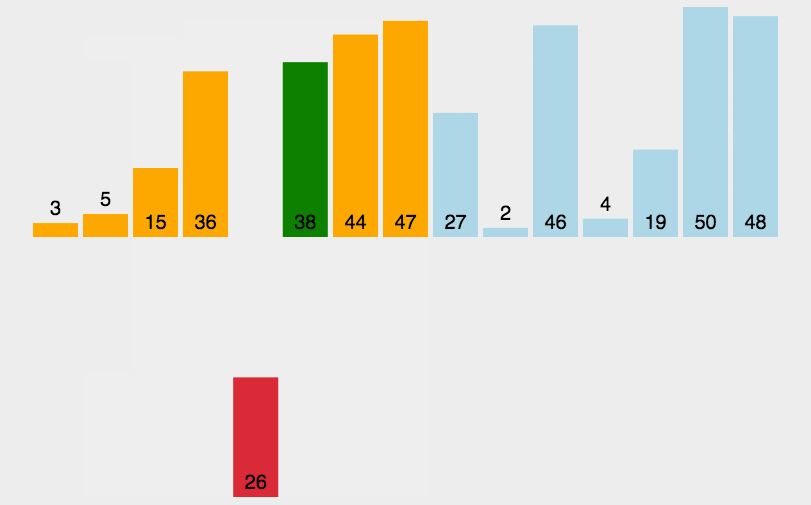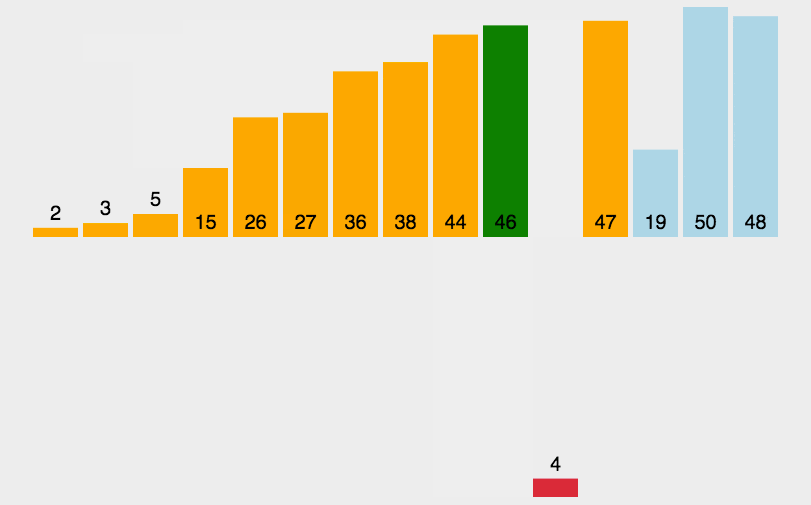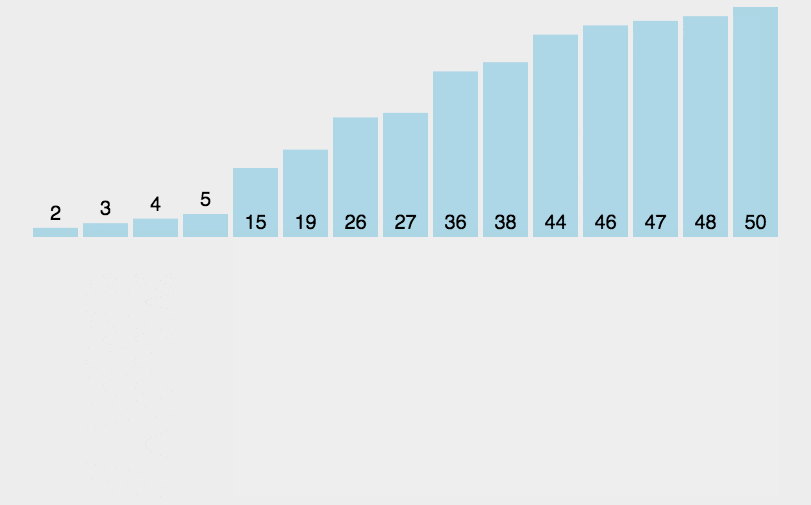
private static int[] insertSort(int[] arr) {
    if (arr == null || arr.length < 2) {
        return arr;
    }
    for (int i = 1; i < arr.length; i++) {
        for (int j = i; j > 0; j--) {
            if (arr[j] < arr[j - 1]) {
                int t = arr[j];
                arr[j] = arr[j - 1];
                arr[j - 1] = t;
            } else {
                break;
            }
        }
    }
    return arr;
}

最好情况，待排序数组已经是升序状态，时间复杂度为O(N) 
最坏情况，待排序数组为反序状态，时间复杂度为O(N^2) 
平均来说，插入排序的时间复杂度为O(N^2) 
空间复杂度为O(1)，是稳定排序 
比较适合待排序数组长度较小且基本有序的情况

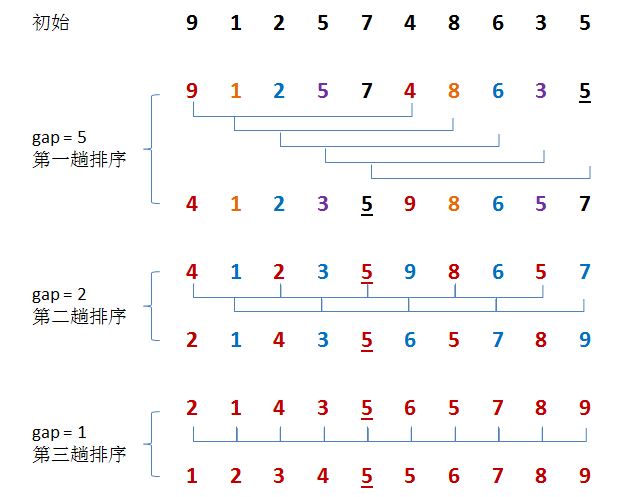
2. 希尔排序

基本思想：把待排序数组分割成若干个较稀疏的子序列，分别进行直接插入排序。经过上述粗略调整，整个序列中的记录已经基本有序，最后再对全部记录进行一次直接插入排序。

public static void shellSort(int[] arr) {
    for (int gap = arr.length / 2; gap > 0; gap /= 2) {
        for (int i = gap; i < arr.length; i++) {
            int j = i;
            int t = arr[j];
            if (arr[j] < arr[j - gap]) {
                while (j - gap >= 0 && t < arr[j - gap]) {
                    arr[j] = arr[j - gap];
                    j -= gap;
                }
                arr[j] = t;
            }
        }
    }
}

最坏情况，时间复杂度为O(N^2) 
最好情况，时间复杂度为O(N^1.3) 
空间复杂度为O(1)，是不稳定排序

交换类排序

1. 冒泡排序 

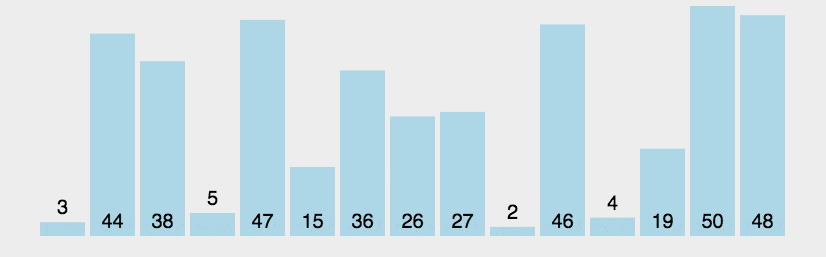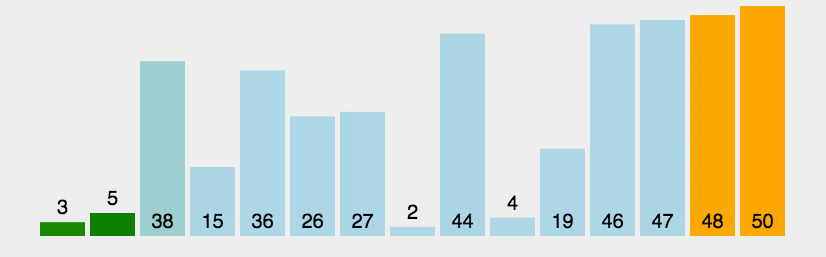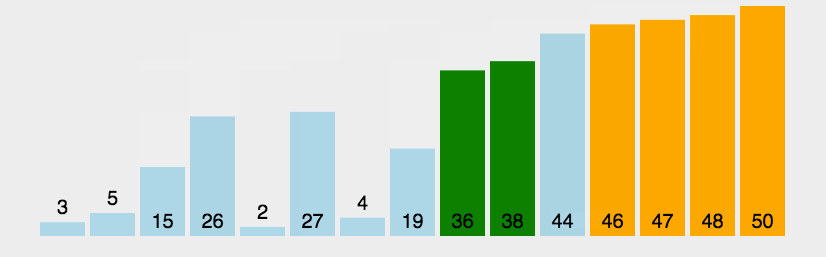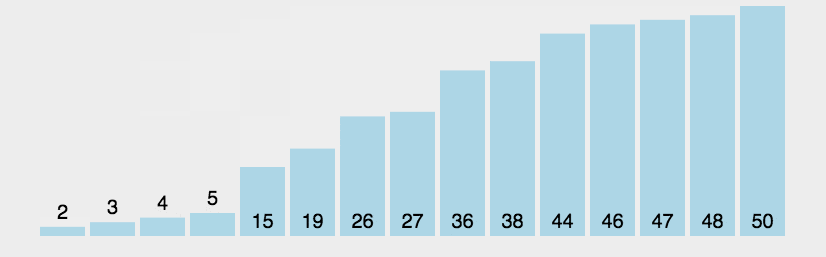
public static void bubbleSort(int[] a) {
    int t = 0;
    for (int i = a.length - 1; i > 0; --i) {
        for (int j = 0; j < i; ++j) {
            if (a[j + 1] < a[j]) {
                t = a[j];
                a[j] = a[j + 1];
                a[j + 1] = t;
            }
        }
    }
}

最好情况，已经升序，时间复杂度为O(N) 
最坏情况和平均情况的时间复杂度都是O(N^2) 
空间复杂度为O(1)，是稳定排序

2. 快速排序

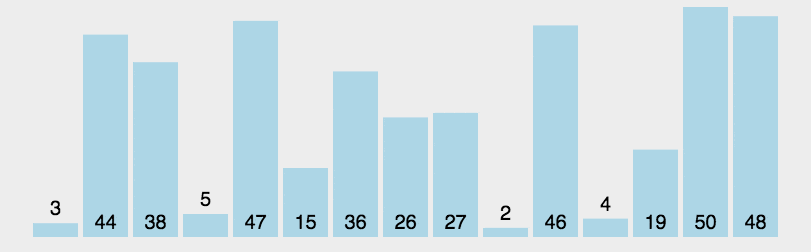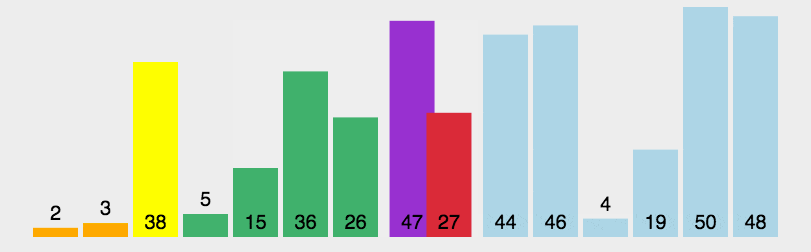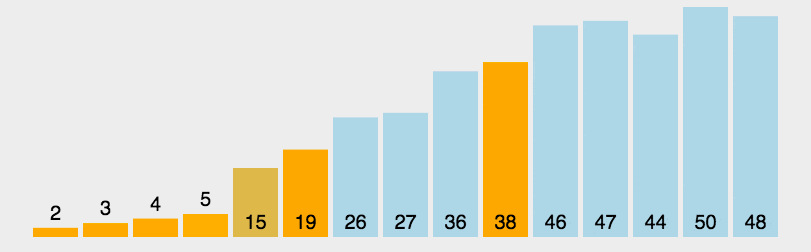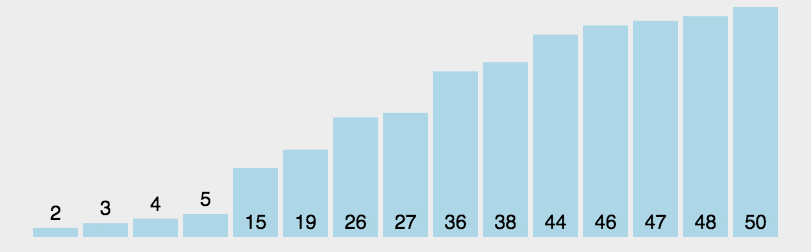
public static void quickSort(int[] arr, int start, int end) {
    if (start < end) {
        int index = partition(arr, start, end);
        quickSort(arr, start, index - 1);
        quickSort(arr, index + 1, end);
    }
}

private static void quickSortByLoop(int[] a, int start, int end) {
    Stack<Integer> stack = new Stack<>();
    if (start < end) {
        stack.push(end);
        stack.push(start);
        while (!stack.isEmpty()) {
            int l = stack.pop();
            int r = stack.pop();
            int index = partition(a, l, r);
            if (l < index - 1) {
                stack.push(index - 1);
                stack.push(l);
            }
            if (r > index + 1) {
                stack.push(r);
                stack.push(index + 1);
            }
        }
    }
}

private static int partition(int[] arr, int start, int end) {
    int pivot = arr[start];
    while (start < end) {
        while (start < end && arr[end] >= pivot) end--;
        arr[start] = arr[end];
        while (start < end && arr[start] <= pivot) start++;
        arr[end] = arr[start];
    }
    arr[start] = pivot;
    return start;
}

最坏情况出现在待排序数组已经为升序状态，时间复杂度为O(N^2) 
最好情况和平均情况的时间复杂度为O(NlogN) 
空间复杂度为O(logN)~O(N)，是不稳定排序

选择类排序 

1. 简单选择排序 

public static void selectSort(int[] a) {
    for (int i = 0; i < a.length; i++) {
        int minIndex = i;
        for (int j = i + 1; j < a.length; j++) {
            if (a[j] < a[minIndex])
                minIndex = j;
        }
        if (minIndex != i) {
            int t = a[i];
            a[i] = a[minIndex];
            a[minIndex] = t;
        }
    }
}

最好最快平均情况的时间复杂度都是O(N^2) 
空间复杂度为O(1)，是否为稳定排序有争议，大部分人认为是不稳定的，[2,2,1]

2. 堆排序

大顶堆：任何非叶子节点的值都大于它的左右孩子的值。 
建堆：从叶子节点找出最大值不断的往上一层冒，最终把最大值冒到顶部根的位置。 

public class HeapSort {
    private static int[] sort = new int[]{1, 0, 10, 20, 3, 5, 6, 4, 9, 8, 12, 17, 34, 11};

    public static void main(String[] args) {
        buildMaxHeapify(sort);
        heapSort(sort);
        print(sort);
    }

    private static void buildMaxHeapify(int[] data) {
        int startIndex = getParentIndex(data.length - 1);
        for (int i = startIndex; i >= 0; i--) {
            maxHeapify(data, data.length, i);
        }
    }

    private static void maxHeapify(int[] data, int heapSize, int index) {
        int left = getChildLeftIndex(index);
        int right = getChildRightIndex(index);
        int largest = index;
        if (left < heapSize && data[index] < data[left]) {
            largest = left;
        }
        if (right < heapSize && data[largest] < data[right]) {
            largest = right;
        }
        if (largest != index) {
            int temp = data[index];
            data[index] = data[largest];
            data[largest] = temp;
            maxHeapify(data, heapSize, largest);
        }
    }

    private static void heapSort(int[] data) {
        for (int i = data.length - 1; i > 0; i--) {
            int temp = data[0];
            data[0] = data[i];
            data[i] = temp;
            maxHeapify(data, i, 0);
        }
    }

    private static int getParentIndex(int current) {
        return (current - 1) >> 1;
    }

    private static int getChildLeftIndex(int current) {
        return (current << 1) + 1;
    }

    private static int getChildRightIndex(int current) {
        return (current << 1) + 2;
    }

    private static void print(int[] data) {
        int pre = -2;
        for (int i = 0; i < data.length; i++) {
            if (pre < (int) getLog(i + 1)) {
                pre = (int) getLog(i + 1);
                System.out.println();
            }
            System.out.print(data[i] + "|");
        }
    }

    private static double getLog(double param) {
        return Math.log(param) / Math.log(2);
    }
}
/*
0|
1|3|
4|5|6|8|
9|10|11|12|17|20|34|
 */

最好最坏平均情况的时间复杂度都是O(NlogN) 
空间复杂度为O(1)，是不稳定排序

---

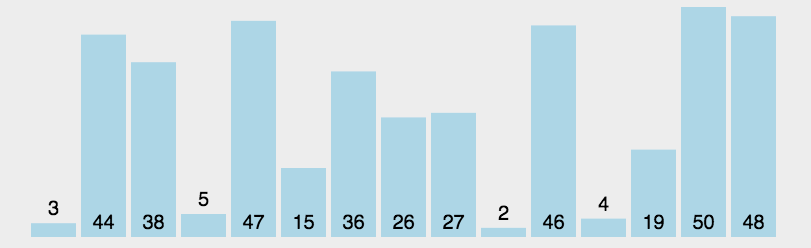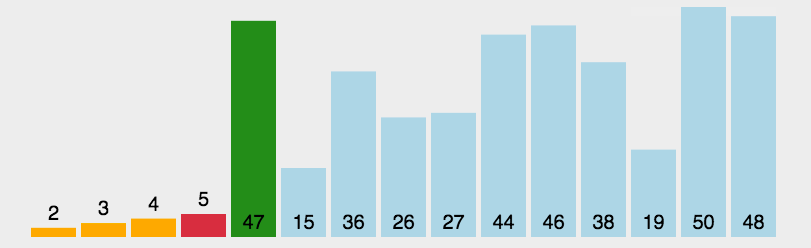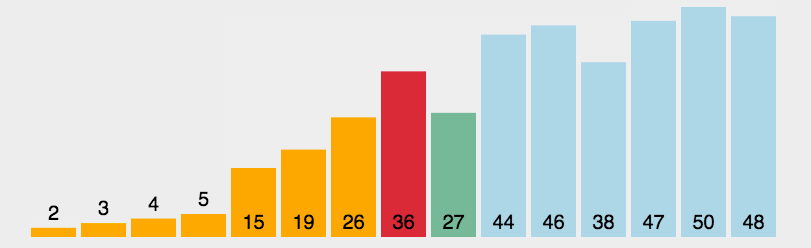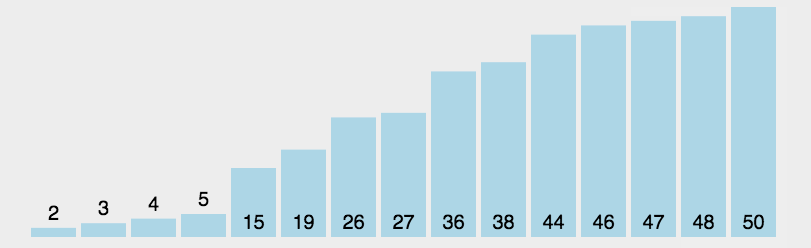
1. 归并排序

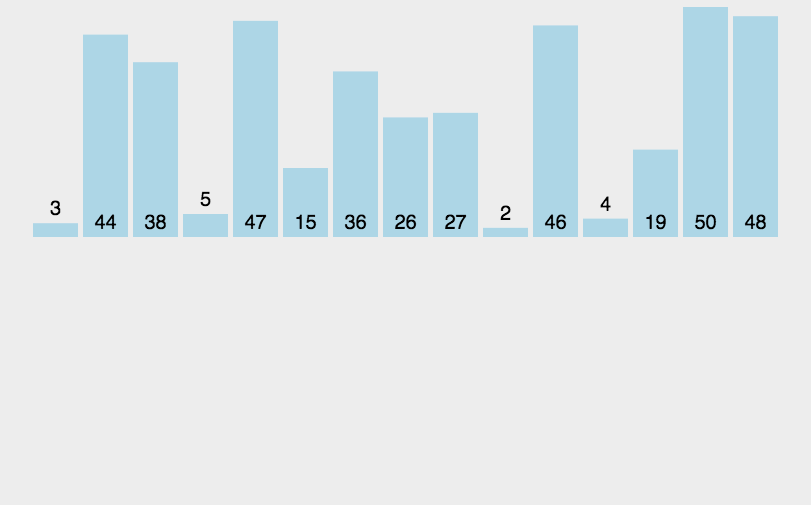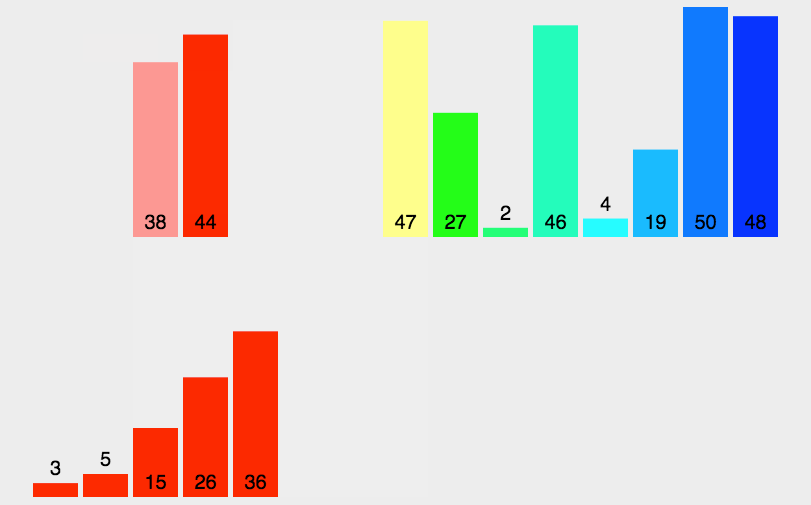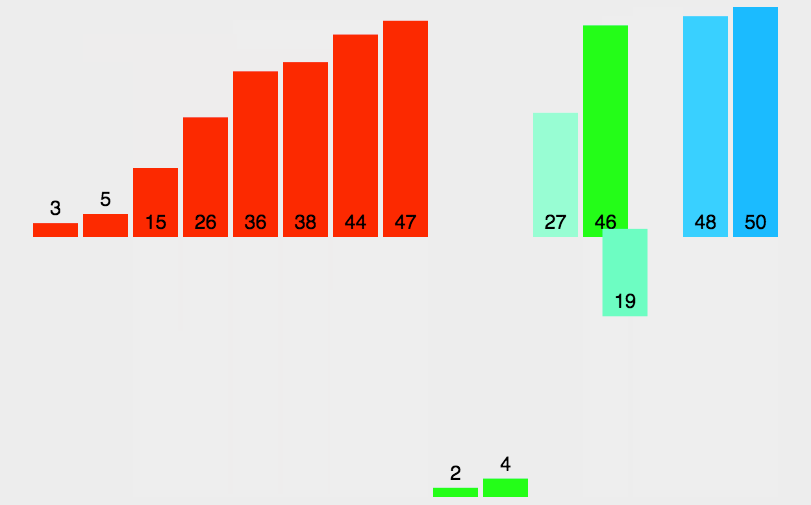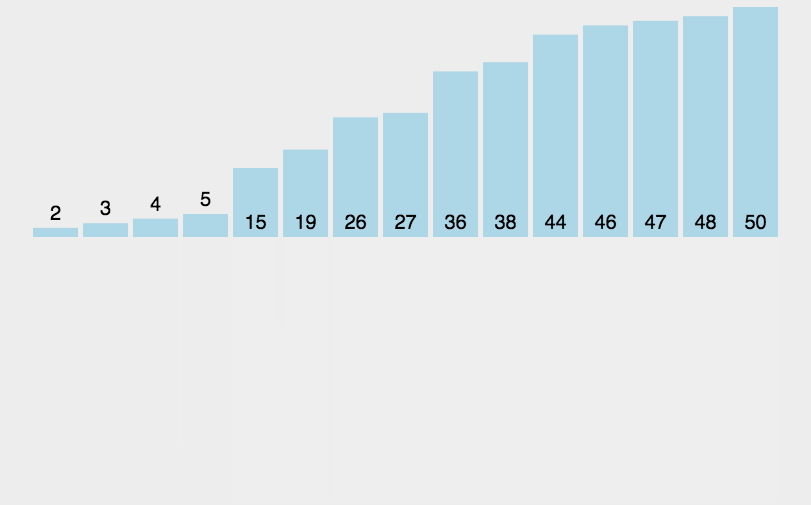
public class Merge {
    public static void main(String[] args) {
        int[] a = {1, 0, 10, 20, 3, 5, 6, 4, 9, 8, 12, 17, 34, 11};
        sort(a);
        for (int x : a)
            System.out.print(x + " ");
    }

    private static int[] aux;

    public static void sort(int[] a) {
        aux = new int[a.length];
        sort(a, 0, a.length - 1);
    }

    private static void sort(int[] a, int lo, int hi) {
        if (hi <= lo) return;
        int mid = lo + (hi - lo) / 2;
        sort(a, lo, mid);
        sort(a, mid + 1, hi);
        merge(a, lo, mid, hi);
    }

    public static void merge(int[] a, int lo, int mid, int hi) {
        int i = lo, j = mid + 1;
        for (int k = lo; k <= hi; k++)
            aux[k] = a[k];
        for (int k = lo; k <= hi; k++)
            if (i > mid) a[k] = aux[j++];
            else if (j > hi) a[k] = aux[i++];
            else if (aux[j] < aux[i]) a[k] = aux[j++];
            else a[k] = aux[i++];
    }
}
/*
0 1 3 4 5 6 8 9 10 11 12 17 20 34 
 */

最好最坏平均情况的时间复杂度都是O(NlogN) 
空间复杂度为O(N)，是稳定排序

2. 基数排序 

public class RadixSort {
    public static void sort(int[] number, int d) {
        int k = 0;
        int n = 1;
        int m = 1;
        int[][] temp = new int[10][number.length];
        int[] order = new int[10];
        while (m <= d) {
            for (int i = 0; i < number.length; i++) {
                int lsd = ((number[i] / n) % 10);
                temp[lsd][order[lsd]] = number[i];
                order[lsd]++;
            }
            for (int i = 0; i < 10; i++) {
                if (order[i] != 0)
                    for (int j = 0; j < order[i]; j++) {
                        number[k] = temp[i][j];
                        k++;
                    }
                order[i] = 0;
            }
            n *= 10;
            k = 0;
            m++;
        }
    }

    public static void main(String[] args) {
        int[] data = {73, 22, 93, 43, 55, 14, 28, 65, 39, 81, 33, 100};
        RadixSort.sort(data, 3);
        for (int i = 0; i < data.length; i++) {
            System.out.print(data[i] + " ");
        }
    }
}
/*
14 22 28 33 39 43 55 65 73 81 93 100
 */

3. 计数排序 

public class CountSort {
    public static void main(String[] args) {
        int a[] = {100, 93, 97, 92, 96, 99, 92, 89, 93, 97, 90, 94, 92, 95};
        int b[] = countSort(a);
        for (int i : b)
            System.out.print(i + " ");
    }

    public static int[] countSort(int[] a) {
        int b[] = new int[a.length];
        int max = a[0], min = a[0];
        for (int i : a) {
            if (i > max) {
                max = i;
            }
            if (i < min) {
                min = i;
            }
        }
        int k = max - min + 1;
        int c[] = new int[k];
        for (int i = 0; i < a.length; ++i) {
            c[a[i] - min] += 1;
        }
        for (int i = 1; i < c.length; ++i) {
            c[i] = c[i] + c[i - 1];
        }
        for (int i = a.length - 1; i >= 0; --i) {
            b[--c[a[i] - min]] = a[i];
        }
        return b;
    }
}
/*
89 90 92 92 92 93 93 94 95 96 97 97 99 100 
 */

各种排序算法性能比较：

---

外排序 

第一阶段是把文件逐段输入到内存，用较好的内排序方法对这段文件进行排序。已排序的文件段通常称为归并段。整个文件经过逐段排序后又逐段写回到外存上。这样，在外存上就形成了许多初始归并段。 
第二阶段是对这些初始归并段使用某种归并方法（如两路归并法），进行多遍归并。最后在外存上形成一个排序的文件。