10.03T2 CDQ分治 codeforces

2、心与心的距离（heart）

就算发一千条短信，心与心的距离也不曾拉近过一厘米。

——《秒速五厘米》

 

题目描述：

那么，怎样才能将两颗心的距离拉近呢？小H独自走在飘雪的街头，思索着这个问题。

他停了下来，用脚尖在雪地上画出一个圈——要拉近心灵的距离，首先肉体上的距离不能太遥远。具体来说，整个世界就是一个数轴，每个人有一个坐标，还有个忍耐值，表示他能忍受的位置范围就是。如果有一个人j，不在这个范围内，那他就输在了距离上。

他又抬起头，看着路灯淡黄的光晕，突然想到：时间！每个人有一个最愿意与他人交往的时刻。两个人i，j，如果，那他们就输在了时间上。

“哦，我懂了”，小H微微一笑。具体来说，两个人i,j可以拉近心灵的距离当且仅且且。

现在请你计算能拉近心灵距离的人的对数。

注意（a，b）,（b，a）只能计算一次。

 

输入格式：

第一行两真整数N，K，含义已在文中给出。

接下来n行，每行三个真整数，含义也已给出。

 

样例输入1：

3 2

3 6 1

7 3 10

10 5 8

 

样例输入2：

5 3

2 4 1

5 1 2

11 10 3

6 5 3

10 5 6

 

样例输出1：

1

样例输出2：

5

 

数据规模与约定：

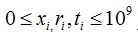，所有互不相同。

 

 

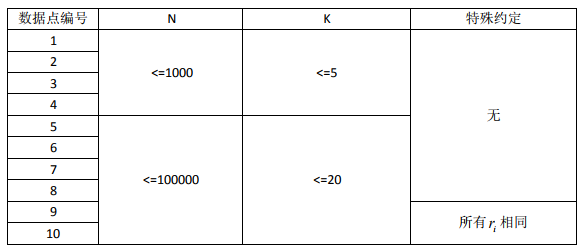
40分：

N^2，不解释了。

code：

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<set>
#define N 1000006
using namespace std;
struct node{
    int x,t,r;
/*    bool operator<(const node&t)const{
        return r<t.r;
    }*/
}e[N];
int main(){
    freopen("heart.in","r",stdin);
    freopen("heart.out","w",stdout);
    int n,k;
    cin>>n>>k;
    for(int i=1;i<=n;i++){
        cin>>e[i].x>>e[i].r>>e[i].t;
    }
    int ans=0;
    if(n<=1000){
        for(int i=1;i<=n;i++){
            for(int j=1;j<=n;j++){
                if(i==j)continue;
                if(abs(e[i].x-e[j].x)>min(e[i].r,e[j].r))continue;
                if(abs(e[i].t-e[j].t)>k)continue;
                ans++;
            }
        }
        cout<<ans/2;
        return 0;
    }
}

最后20分：

其实这部分数据对你想出正解有一定提示作用，因为它告诉了你r是个比较重要的因素。

100分：

我们发现，对一个人i，如果我们既要考虑在i的忍受范围内的人，又要考虑这些人中，i又在哪些人的忍受范围之内，就特别难做。

对于两个人i,j,我们设，如果j在i的忍受范围之内，那么显然i也在j的忍受范围之内。所以我们先按r排序，这样，对于i,j（i<j）我们这需要考虑j是否在i的忍受范围之内就可以了。

具体做法有很多，我用的CDQ。先按r排序，然后递归下去，处理完左右区间后再分别按t排序处理。

CDQ的思想其实与归并排序有几分相似，在下面的代码里实际上左半边的R一定比右半边大，所以可以进行转移，因为两边的t都是有序的，所以找出来的符合t

条件的序列一定是连续的，我们选完t之后用树状数组维护一下编号就可以了，然后归并的时候就要按照t进行排序

 code：

#include<iostream>
#include<cstdio>
#include<algorithm>
#define N 1000005
#define tiao puts("!");
using namespace std;
struct node{
    int x,R,t,l,r;
}e[N];
int ans,cc;
int c[N],d[N],tot;
bool cmp(node a,node b){
    return a.R<b.R;
}
int lowbit(int x){
    return x&(-x);
}
void add(int x,int v){
    while(x<=cc){
    //    cout<<"now->"<<x<<endl;
        c[x]+=v;
        x+=lowbit(x);
    }
}
int n,k;
int query(int x){
    int ans0=0;
    while(x){
        ans0+=c[x];
        x-=lowbit(x);
    }
    return ans0;
}
bool bmp(const node &a,const node &b){
    return a.t<b.t;
}
void clear(int x){
    while(x<=cc){
        c[x]=0;
        x+=lowbit(x);
    }
}
void cdq(int l,int r){
    //cout<<"left="<<l<<"  right="<<r<<endl;
    if(l==r)return;
    int mid=l+r>>1;
    cdq(l,mid);cdq(mid+1,r);//处理左右区间 
    int head=mid+1,tail=mid;//找区间，现在是空集 
    for(int i=l;i<=mid;i++){//找左边 ，因为右边的R是要比左边大的，所以右边一定可以忍受左边，避免了重复计数 
        while(tail<r&&e[tail+1].t-e[i].t<=k){//找右边界 
            tail++;
            add(e[tail].x,1);
        }
        while(head<=tail&&e[i].t-e[head].t>k){//找左边界 
            add(e[head].x,-1);
            head++; 
        }
        ans+=query(e[i].r)-query(e[i].l-1);
    }
    for(int i=mid+1;i<=r;i++)clear(e[i].x);
    inplace_merge(e+l,e+mid+1,e+r+1,bmp);
//    cout<<ans;
}
int main(){
    freopen("heart.in","r",stdin);
    freopen("heart.out","w",stdout);
    cin>>n>>k;
    for(int i=1;i<=n;i++){
        cin>>e[i].x>>e[i].R>>e[i].t;
        d[++tot]=e[i].x-e[i].R;
        d[++tot]=e[i].x;
        d[++tot]=e[i].x+e[i].R;
    }
    sort(d+1,d+tot+1);
    cc=unique(d+1,d+tot+1)-d;    
    for(int i=1;i<=n;i++){
        e[i].l=lower_bound(d+1,d+cc,e[i].x-e[i].R)-d;
        e[i].r=lower_bound(d+1,d+cc,e[i].x+e[i].R)-d;
        e[i].x=lower_bound(d+1,d+cc,e[i].x)-d;
    }
    sort(e+1,e+n+1,cmp);
    cdq(1,n);
    cout<<ans;
    return 0;
}