9.26T3
3.孤独
(loneliness)
【问题描述】
【输入】
【输出】
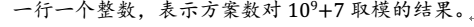
【样例输入】
2
2 3 4
1 2 3
【样例输出】
31
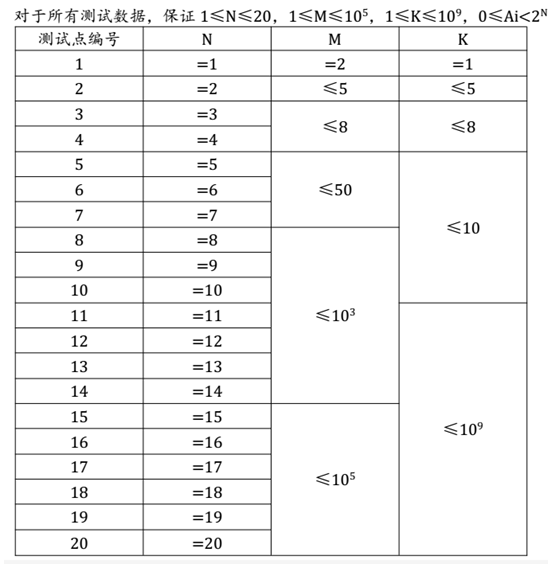
【数据范围与约定】
虽然一眼知道这就是容斥原理，但是菜鸡的我没有枚举子集求解，实际上这是一道非常好的子集转移的题目，可以作为一个经典题目来处理
70 分做法
我们用另一种思路统计答案。
Ans=选择第一个话题能交流的人数的k次方+选择第二个话题交流的人数的k次方+……
-选择一二两个话题都能交流的人数的 k 次方+…
那么我们现在可以用 2 的 n 次方来枚举选择哪几个话题，并统计出当前选择话题个数对
答案的贡献的正负。
统计“选择某些话题都能交流的人数”只要暴力枚举每个人，
并判断这个人交流的话题是否包含该集合。
复杂度 2^n*m
100 分做法
此时复杂度的瓶颈在于子集转移，
那么就要实现子集转移的优化
再次换一个思路。一个人对答案的贡献实际是他能选择的话题的子集。
举个例子：某个人 01011
那么“选择二四两个话题都能交流的人数”就会＋1
所有他的子集都会＋1
那么我们只要枚举子集就行了。
一般的写法是 n*3^n，
一种优雅的方法可以在 n*2^n 时间内转移子集。
考虑我们做的事情其实就是把 1 位的转移到 0 位上，
那么我们依次对每一位进行这样的操作即可。
code：
1 #include<iostream> 2 #include<cstdio> 3 using namespace std; 4 const long long mod=1e9+7; 5 long long n,m,k; 6 long long ans; 7 long long s[50000004]; 8 long long power(long long a,long long b){ 9 long long t=a,ans0=1; 10 for(;b;b>>=1){ 11 if(b&1){ 12 ans0*=t; 13 ans0%=mod; 14 } 15 t*=t; 16 t%=mod; 17 } 18 return ans0; 19 } 20 void dfs(long long x,long long dep){//这就是容斥原理的过程 21 if(dep==n){//如果这个数字已经被确定了0，1 22 long long temp=x,now=0; 23 for(;temp;temp>>=1)//计算有多少个兴趣 24 if(temp&1)now++; 25 if(x==0)return;//0必须要排除在外，因为会减掉所有的答案 26 if(now%2==0)ans-=power(s[x],k);//如果有偶数个兴趣，把么就要减掉 27 else ans+=power(s[x],k);//反之就是必须要加上去 28 ans+=mod; 29 ans%=mod; 30 return; 31 } 32 dfs(x<<1|1,dep+1); 33 dfs(x<<1,dep+1); 34 } 35 int main(){ 36 freopen("loneliness.in","r",stdin); 37 freopen("loneliness.out","w",stdout); 38 long long num;cin>>num; 39 cin>>n>>m>>k; 40 for(long long i=1;i<=m;i++){//自己现在的状态实际上就是包含自己的 41 long long x; 42 cin>>x; 43 s[x]++; 44 } 45 for(long long i=0;i<n;i++){//枚举兴趣 46 for(long long j=0;j<=(1<<n+1)-1;j++){//枚举子集 47 if(j&(1<<i))//如果拥有这个兴趣 48 s[j^(1<<i)]+=s[j];//那么虽然没有这个兴趣，但是有其他跟他拥有共同兴趣的人就可以被包含了，也就是我们以后转移的条件 49 } 50 } 51 // for(long long i=1;i<=3;i++)cout<<s[i]<<endl; 52 dfs(0,0); 53 cout<<ans; 54 return 0; 55 }
over
